PhysicsCorrect: A Training-Free Approach for Stable Neural PDE Simulations

Neural networks have emerged as powerful surrogates for solving partial differential equations (PDEs), offering significant computational speedups over traditional methods. However, these models suffer from a critical limitation: error accumulation during long-term rollouts, where small inaccuracies compound exponentially, eventually causing complete divergence from physically valid solutions. We present PhysicsCorrect, a training-free correction framework that enforces PDE consistency at each prediction step by formulating correction as a linearized inverse problem based on PDE residuals. Our key innovation is an efficient caching strategy that precomputes the Jacobian and its pseudoinverse during an offline warm-up phase, reducing computational overhead by two orders of magnitude compared to standard correction approaches. Across three representative PDE systems -- Navier-Stokes fluid dynamics, wave equations, and the chaotic Kuramoto-Sivashinsky equation -- PhysicsCorrect reduces prediction errors by up to 100x while adding negligible inference time (under 5\%). The framework integrates seamlessly with diverse architectures including Fourier Neural Operators, UNets, and Vision Transformers, effectively transforming unstable neural surrogates into reliable simulation tools that bridge the gap between deep learning's computational efficiency and the physical fidelity demanded by practical scientific applications.

Active Learning Design: Modeling Force Output for Axisymmetric Soft Pneumatic Actuators

Soft pneumatic actuators (SPA) made from elastomeric materials can provide large strain and large force. The behavior of locally strain-restricted hyperelastic materials under inflation has been investigated thoroughly for shape reconfiguration, but requires further investigation for trajectories involving external force. In this work we model force-pressure-height relationships for a concentrically strain-limited class of soft pneumatic actuators and demonstrate the use of this model to design SPA response for object lifting. We predict relationships under different loadings by solving energy minimization equations and verify this theory by using an automated test rig to collect rich data for n=22 Ecoflex 00-30 membranes. We collect this data using an active learning pipeline to efficiently model the design space. We show that this learned material model outperforms the theory-based model and naive curve-fitting approaches. We use our model to optimize membrane design for different lift tasks and compare this performance to other designs. These contributions represent a step towards understanding the natural response for this class of actuator and embodying intelligent lifts in a single-pressure input actuator system.

On conditional diffusion models for PDE simulations

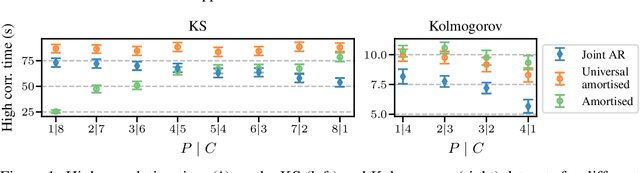
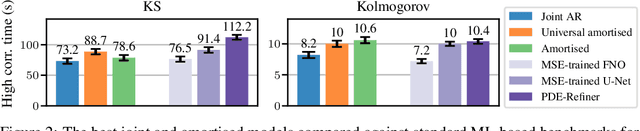
Modelling partial differential equations (PDEs) is of crucial importance in science and engineering, and it includes tasks ranging from forecasting to inverse problems, such as data assimilation. However, most previous numerical and machine learning approaches that target forecasting cannot be applied out-of-the-box for data assimilation. Recently, diffusion models have emerged as a powerful tool for conditional generation, being able to flexibly incorporate observations without retraining. In this work, we perform a comparative study of score-based diffusion models for forecasting and assimilation of sparse observations. In particular, we focus on diffusion models that are either trained in a conditional manner, or conditioned after unconditional training. We address the shortcomings of existing models by proposing 1) an autoregressive sampling approach that significantly improves performance in forecasting, 2) a new training strategy for conditional score-based models that achieves stable performance over a range of history lengths, and 3) a hybrid model which employs flexible pre-training conditioning on initial conditions and flexible post-training conditioning to handle data assimilation. We empirically show that these modifications are crucial for successfully tackling the combination of forecasting and data assimilation, a task commonly encountered in real-world scenarios.

Score Neural Operator: A Generative Model for Learning and Generalizing Across Multiple Probability Distributions

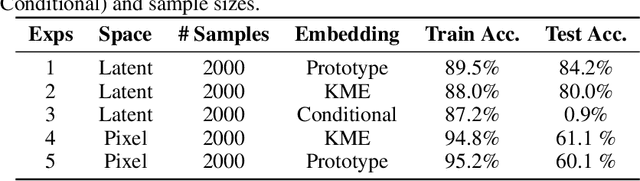
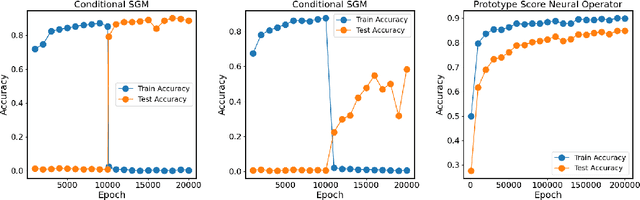
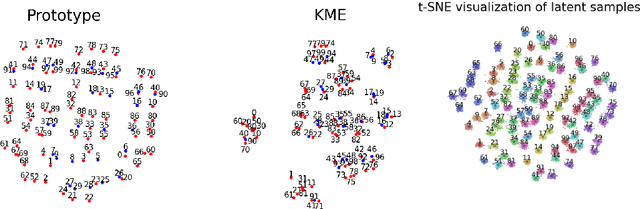
Most existing generative models are limited to learning a single probability distribution from the training data and cannot generalize to novel distributions for unseen data. An architecture that can generate samples from both trained datasets and unseen probability distributions would mark a significant breakthrough. Recently, score-based generative models have gained considerable attention for their comprehensive mode coverage and high-quality image synthesis, as they effectively learn an operator that maps a probability distribution to its corresponding score function. In this work, we introduce the $\emph{Score Neural Operator}$, which learns the mapping from multiple probability distributions to their score functions within a unified framework. We employ latent space techniques to facilitate the training of score matching, which tends to over-fit in the original image pixel space, thereby enhancing sample generation quality. Our trained Score Neural Operator demonstrates the ability to predict score functions of probability measures beyond the training space and exhibits strong generalization performance in both 2-dimensional Gaussian Mixture Models and 1024-dimensional MNIST double-digit datasets. Importantly, our approach offers significant potential for few-shot learning applications, where a single image from a new distribution can be leveraged to generate multiple distinct images from that distribution.

Deep Learning Alternatives of the Kolmogorov Superposition Theorem

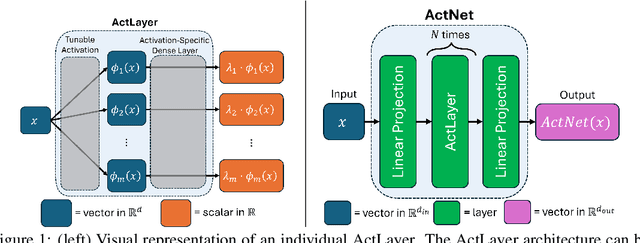
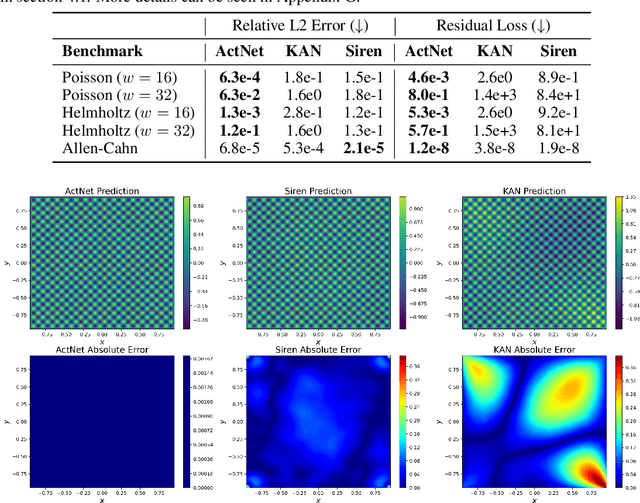
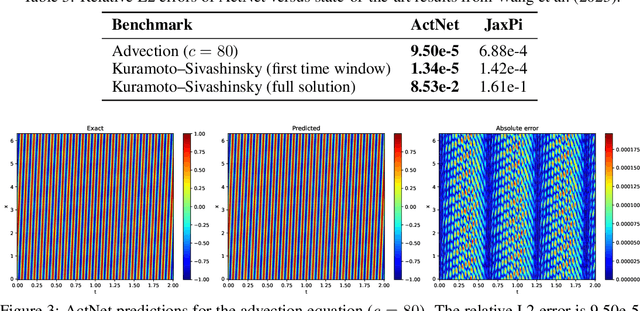
This paper explores alternative formulations of the Kolmogorov Superposition Theorem (KST) as a foundation for neural network design. The original KST formulation, while mathematically elegant, presents practical challenges due to its limited insight into the structure of inner and outer functions and the large number of unknown variables it introduces. Kolmogorov-Arnold Networks (KANs) leverage KST for function approximation, but they have faced scrutiny due to mixed results compared to traditional multilayer perceptrons (MLPs) and practical limitations imposed by the original KST formulation. To address these issues, we introduce ActNet, a scalable deep learning model that builds on the KST and overcomes many of the drawbacks of Kolmogorov's original formulation. We evaluate ActNet in the context of Physics-Informed Neural Networks (PINNs), a framework well-suited for leveraging KST's strengths in low-dimensional function approximation, particularly for simulating partial differential equations (PDEs). In this challenging setting, where models must learn latent functions without direct measurements, ActNet consistently outperforms KANs across multiple benchmarks and is competitive against the current best MLP-based approaches. These results present ActNet as a promising new direction for KST-based deep learning applications, particularly in scientific computing and PDE simulation tasks.

Disk2Planet: A Robust and Automated Machine Learning Tool for Parameter Inference in Disk-Planet Systems

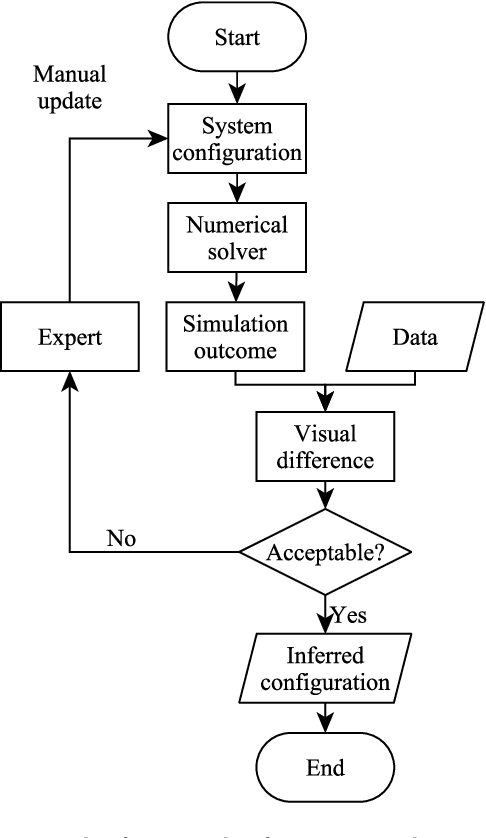
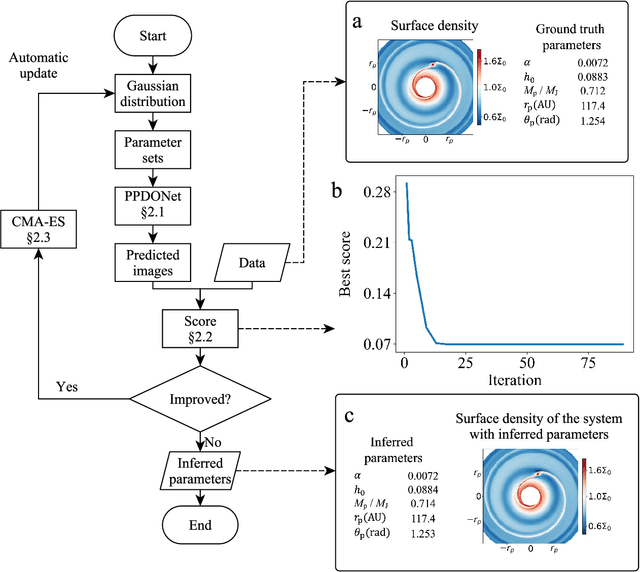
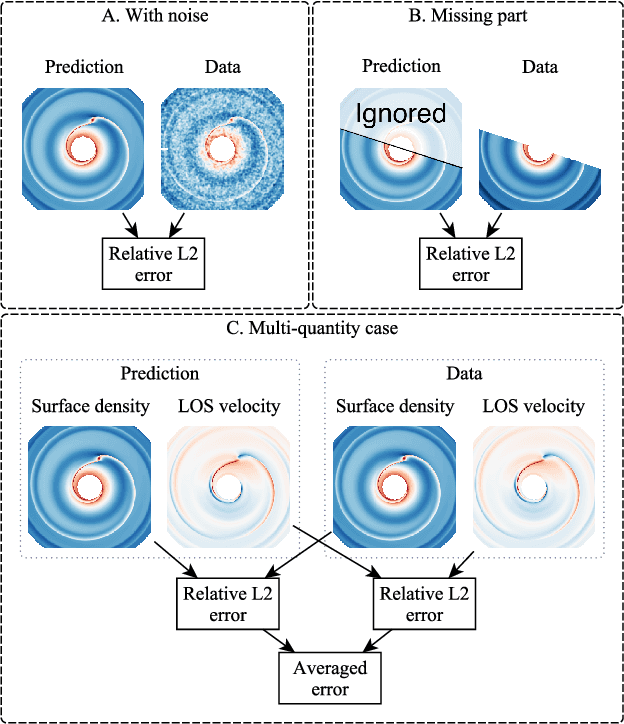
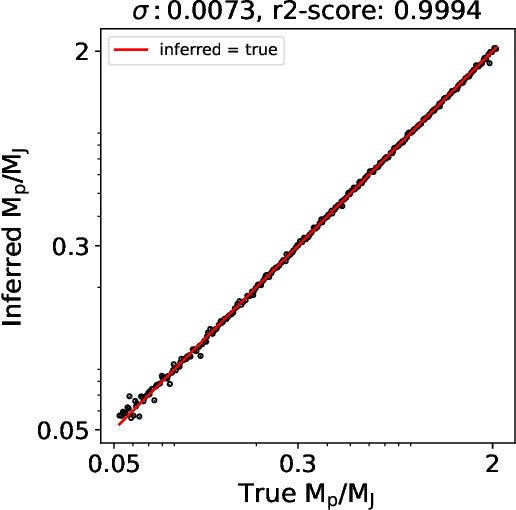
We introduce Disk2Planet, a machine learning-based tool to infer key parameters in disk-planet systems from observed protoplanetary disk structures. Disk2Planet takes as input the disk structures in the form of two-dimensional density and velocity maps, and outputs disk and planet properties, that is, the Shakura--Sunyaev viscosity, the disk aspect ratio, the planet--star mass ratio, and the planet's radius and azimuth. We integrate the Covariance Matrix Adaptation Evolution Strategy (CMA--ES), an evolutionary algorithm tailored for complex optimization problems, and the Protoplanetary Disk Operator Network (PPDONet), a neural network designed to predict solutions of disk--planet interactions. Our tool is fully automated and can retrieve parameters in one system in three minutes on an Nvidia A100 graphics processing unit. We empirically demonstrate that our tool achieves percent-level or higher accuracy, and is able to handle missing data and unknown levels of noise.

Physics-Informed Neural Networks and Extensions

In this paper, we review the new method Physics-Informed Neural Networks (PINNs) that has become the main pillar in scientific machine learning, we present recent practical extensions, and provide a specific example in data-driven discovery of governing differential equations.

Bridging Operator Learning and Conditioned Neural Fields: A Unifying Perspective

Operator learning is an emerging area of machine learning which aims to learn mappings between infinite dimensional function spaces. Here we uncover a connection between operator learning architectures and conditioned neural fields from computer vision, providing a unified perspective for examining differences between popular operator learning models. We find that many commonly used operator learning models can be viewed as neural fields with conditioning mechanisms restricted to point-wise and/or global information. Motivated by this, we propose the Continuous Vision Transformer (CViT), a novel neural operator architecture that employs a vision transformer encoder and uses cross-attention to modulate a base field constructed with a trainable grid-based positional encoding of query coordinates. Despite its simplicity, CViT achieves state-of-the-art results across challenging benchmarks in climate modeling and fluid dynamics. Our contributions can be viewed as a first step towards adapting advanced computer vision architectures for building more flexible and accurate machine learning models in physical sciences.

Aurora: A Foundation Model of the Atmosphere

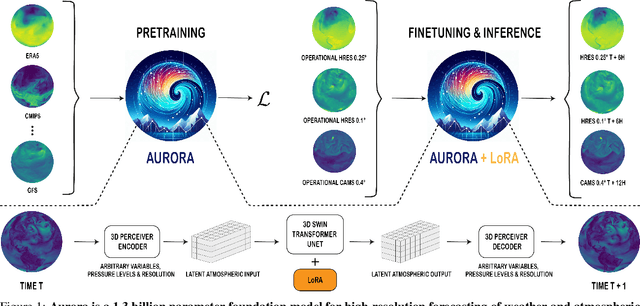
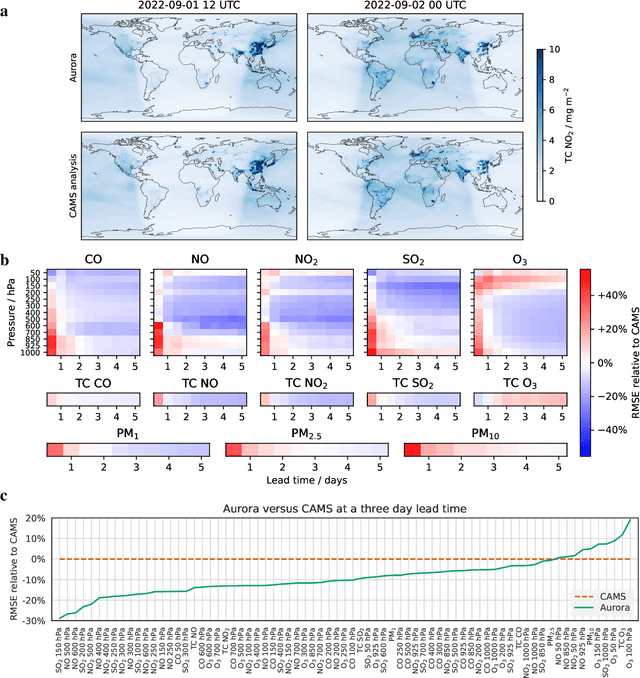
Deep learning foundation models are revolutionizing many facets of science by leveraging vast amounts of data to learn general-purpose representations that can be adapted to tackle diverse downstream tasks. Foundation models hold the promise to also transform our ability to model our planet and its subsystems by exploiting the vast expanse of Earth system data. Here we introduce Aurora, a large-scale foundation model of the atmosphere trained on over a million hours of diverse weather and climate data. Aurora leverages the strengths of the foundation modelling approach to produce operational forecasts for a wide variety of atmospheric prediction problems, including those with limited training data, heterogeneous variables, and extreme events. In under a minute, Aurora produces 5-day global air pollution predictions and 10-day high-resolution weather forecasts that outperform state-of-the-art classical simulation tools and the best specialized deep learning models. Taken together, these results indicate that foundation models can transform environmental forecasting.

Composite Bayesian Optimization In Function Spaces Using NEON -- Neural Epistemic Operator Networks

Operator learning is a rising field of scientific computing where inputs or outputs of a machine learning model are functions defined in infinite-dimensional spaces. In this paper, we introduce NEON (Neural Epistemic Operator Networks), an architecture for generating predictions with uncertainty using a single operator network backbone, which presents orders of magnitude less trainable parameters than deep ensembles of comparable performance. We showcase the utility of this method for sequential decision-making by examining the problem of composite Bayesian Optimization (BO), where we aim to optimize a function $f=g\circ h$, where $h:X\to C(\mathcal{Y},\mathbb{R}^{d_s})$ is an unknown map which outputs elements of a function space, and $g: C(\mathcal{Y},\mathbb{R}^{d_s})\to \mathbb{R}$ is a known and cheap-to-compute functional. By comparing our approach to other state-of-the-art methods on toy and real world scenarios, we demonstrate that NEON achieves state-of-the-art performance while requiring orders of magnitude less trainable parameters.