Score Neural Operator: A Generative Model for Learning and Generalizing Across Multiple Probability Distributions
Paper and Code
Oct 11, 2024
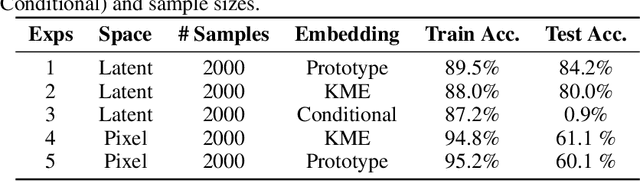
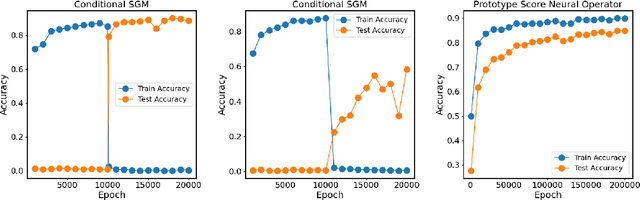
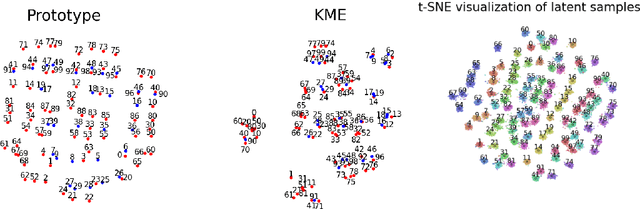
Most existing generative models are limited to learning a single probability distribution from the training data and cannot generalize to novel distributions for unseen data. An architecture that can generate samples from both trained datasets and unseen probability distributions would mark a significant breakthrough. Recently, score-based generative models have gained considerable attention for their comprehensive mode coverage and high-quality image synthesis, as they effectively learn an operator that maps a probability distribution to its corresponding score function. In this work, we introduce the $\emph{Score Neural Operator}$, which learns the mapping from multiple probability distributions to their score functions within a unified framework. We employ latent space techniques to facilitate the training of score matching, which tends to over-fit in the original image pixel space, thereby enhancing sample generation quality. Our trained Score Neural Operator demonstrates the ability to predict score functions of probability measures beyond the training space and exhibits strong generalization performance in both 2-dimensional Gaussian Mixture Models and 1024-dimensional MNIST double-digit datasets. Importantly, our approach offers significant potential for few-shot learning applications, where a single image from a new distribution can be leveraged to generate multiple distinct images from that distribution.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge