Score Neural Operator: A Generative Model for Learning and Generalizing Across Multiple Probability Distributions

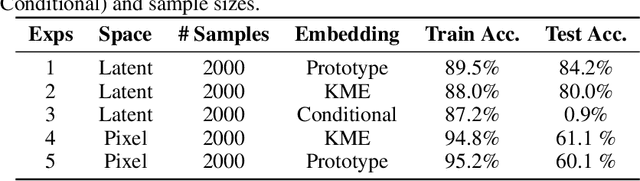
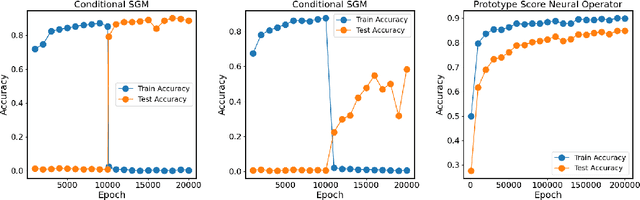
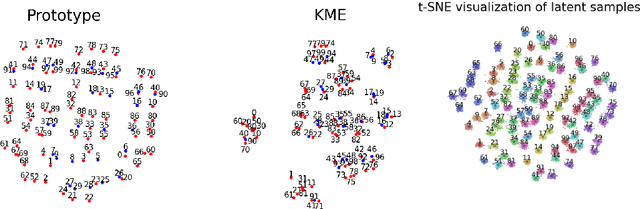
Most existing generative models are limited to learning a single probability distribution from the training data and cannot generalize to novel distributions for unseen data. An architecture that can generate samples from both trained datasets and unseen probability distributions would mark a significant breakthrough. Recently, score-based generative models have gained considerable attention for their comprehensive mode coverage and high-quality image synthesis, as they effectively learn an operator that maps a probability distribution to its corresponding score function. In this work, we introduce the $\emph{Score Neural Operator}$, which learns the mapping from multiple probability distributions to their score functions within a unified framework. We employ latent space techniques to facilitate the training of score matching, which tends to over-fit in the original image pixel space, thereby enhancing sample generation quality. Our trained Score Neural Operator demonstrates the ability to predict score functions of probability measures beyond the training space and exhibits strong generalization performance in both 2-dimensional Gaussian Mixture Models and 1024-dimensional MNIST double-digit datasets. Importantly, our approach offers significant potential for few-shot learning applications, where a single image from a new distribution can be leveraged to generate multiple distinct images from that distribution.

Gaussian Process Port-Hamiltonian Systems: Bayesian Learning with Physics Prior

Data-driven approaches achieve remarkable results for the modeling of complex dynamics based on collected data. However, these models often neglect basic physical principles which determine the behavior of any real-world system. This omission is unfavorable in two ways: The models are not as data-efficient as they could be by incorporating physical prior knowledge, and the model itself might not be physically correct. We propose Gaussian Process Port-Hamiltonian systems (GP-PHS) as a physics-informed Bayesian learning approach with uncertainty quantification. The Bayesian nature of GP-PHS uses collected data to form a distribution over all possible Hamiltonians instead of a single point estimate. Due to the underlying physics model, a GP-PHS generates passive systems with respect to designated inputs and outputs. Further, the proposed approach preserves the compositional nature of Port-Hamiltonian systems.

Learning Operators with Coupled Attention

Supervised operator learning is an emerging machine learning paradigm with applications to modeling the evolution of spatio-temporal dynamical systems and approximating general black-box relationships between functional data. We propose a novel operator learning method, LOCA (Learning Operators with Coupled Attention), motivated from the recent success of the attention mechanism. In our architecture, the input functions are mapped to a finite set of features which are then averaged with attention weights that depend on the output query locations. By coupling these attention weights together with an integral transform, LOCA is able to explicitly learn correlations in the target output functions, enabling us to approximate nonlinear operators even when the number of output function in the training set measurements is very small. Our formulation is accompanied by rigorous approximation theoretic guarantees on the universal expressiveness of the proposed model. Empirically, we evaluate the performance of LOCA on several operator learning scenarios involving systems governed by ordinary and partial differential equations, as well as a black-box climate prediction problem. Through these scenarios we demonstrate state of the art accuracy, robustness with respect to noisy input data, and a consistently small spread of errors over testing data sets, even for out-of-distribution prediction tasks.