Score Neural Operator: A Generative Model for Learning and Generalizing Across Multiple Probability Distributions

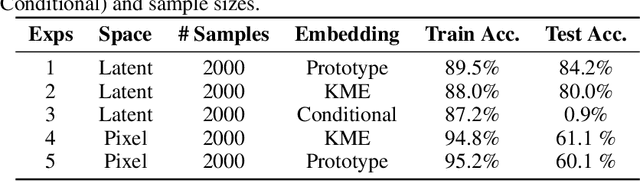
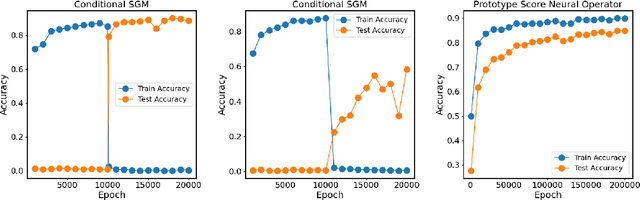
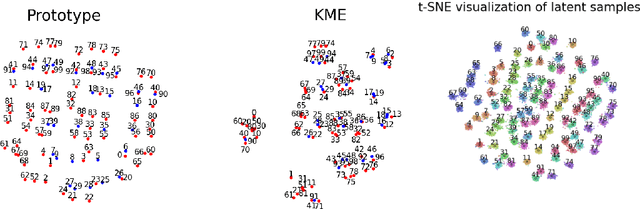
Most existing generative models are limited to learning a single probability distribution from the training data and cannot generalize to novel distributions for unseen data. An architecture that can generate samples from both trained datasets and unseen probability distributions would mark a significant breakthrough. Recently, score-based generative models have gained considerable attention for their comprehensive mode coverage and high-quality image synthesis, as they effectively learn an operator that maps a probability distribution to its corresponding score function. In this work, we introduce the $\emph{Score Neural Operator}$, which learns the mapping from multiple probability distributions to their score functions within a unified framework. We employ latent space techniques to facilitate the training of score matching, which tends to over-fit in the original image pixel space, thereby enhancing sample generation quality. Our trained Score Neural Operator demonstrates the ability to predict score functions of probability measures beyond the training space and exhibits strong generalization performance in both 2-dimensional Gaussian Mixture Models and 1024-dimensional MNIST double-digit datasets. Importantly, our approach offers significant potential for few-shot learning applications, where a single image from a new distribution can be leveraged to generate multiple distinct images from that distribution.

Evaluating and Modeling Social Intelligence: A Comparative Study of Human and AI Capabilities

Facing the current debate on whether Large Language Models (LLMs) attain near-human intelligence levels (Mitchell & Krakauer, 2023; Bubeck et al., 2023; Kosinski, 2023; Shiffrin & Mitchell, 2023; Ullman, 2023), the current study introduces a benchmark for evaluating social intelligence, one of the most distinctive aspects of human cognition. We developed a comprehensive theoretical framework for social dynamics and introduced two evaluation tasks: Inverse Reasoning (IR) and Inverse Inverse Planning (IIP). Our approach also encompassed a computational model based on recursive Bayesian inference, adept at elucidating diverse human behavioral patterns. Extensive experiments and detailed analyses revealed that humans surpassed the latest GPT models in overall performance, zero-shot learning, one-shot generalization, and adaptability to multi-modalities. Notably, GPT models demonstrated social intelligence only at the most basic order (order = 0), in stark contrast to human social intelligence (order >= 2). Further examination indicated a propensity of LLMs to rely on pattern recognition for shortcuts, casting doubt on their possession of authentic human-level social intelligence. Our codes, dataset, appendix and human data are released at https://github.com/bigai-ai/Evaluate-n-Model-Social-Intelligence.

CivRealm: A Learning and Reasoning Odyssey in Civilization for Decision-Making Agents

The generalization of decision-making agents encompasses two fundamental elements: learning from past experiences and reasoning in novel contexts. However, the predominant emphasis in most interactive environments is on learning, often at the expense of complexity in reasoning. In this paper, we introduce CivRealm, an environment inspired by the Civilization game. Civilization's profound alignment with human history and society necessitates sophisticated learning, while its ever-changing situations demand strong reasoning to generalize. Particularly, CivRealm sets up an imperfect-information general-sum game with a changing number of players; it presents a plethora of complex features, challenging the agent to deal with open-ended stochastic environments that require diplomacy and negotiation skills. Within CivRealm, we provide interfaces for two typical agent types: tensor-based agents that focus on learning, and language-based agents that emphasize reasoning. To catalyze further research, we present initial results for both paradigms. The canonical RL-based agents exhibit reasonable performance in mini-games, whereas both RL- and LLM-based agents struggle to make substantial progress in the full game. Overall, CivRealm stands as a unique learning and reasoning challenge for decision-making agents. The code is available at https://github.com/bigai-ai/civrealm.

Exploring General Intelligence via Gated Graph Transformer in Functional Connectivity Studies

Functional connectivity (FC) as derived from fMRI has emerged as a pivotal tool in elucidating the intricacies of various psychiatric disorders and delineating the neural pathways that underpin cognitive and behavioral dynamics inherent to the human brain. While Graph Neural Networks (GNNs) offer a structured approach to represent neuroimaging data, they are limited by their need for a predefined graph structure to depict associations between brain regions, a detail not solely provided by FCs. To bridge this gap, we introduce the Gated Graph Transformer (GGT) framework, designed to predict cognitive metrics based on FCs. Empirical validation on the Philadelphia Neurodevelopmental Cohort (PNC) underscores the superior predictive prowess of our model, further accentuating its potential in identifying pivotal neural connectivities that correlate with human cognitive processes.

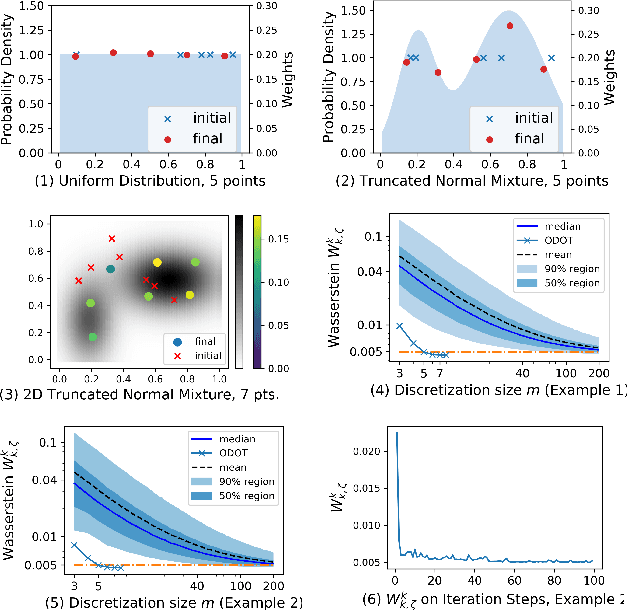
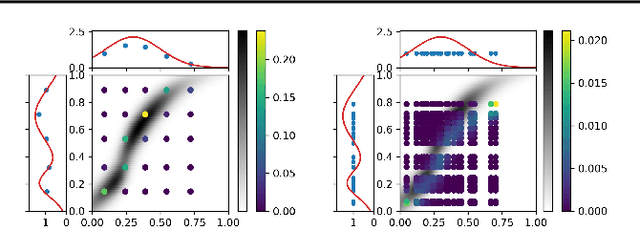
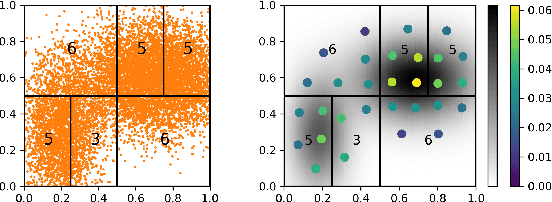
Efficient Discretizations of Optimal Transport

Obtaining solutions to Optimal Transportation (OT) problems is typically intractable when the marginal spaces are continuous. Recent research has focused on approximating continuous solutions with discretization methods based on i.i.d. sampling, and has proven convergence as the sample size increases. However, obtaining OT solutions with large sample sizes requires intensive computation effort, that can be prohibitive in practice. In this paper, we propose an algorithm for calculating discretizations with a given number of points for marginal distributions, by minimizing the (entropy-regularized) Wasserstein distance, and result in plans that are comparable to those obtained with much larger numbers of i.i.d. samples. Moreover, a local version of such discretizations which is parallelizable for large scale applications is proposed. We prove bounds for our approximation and demonstrate performance on a wide range of problems.

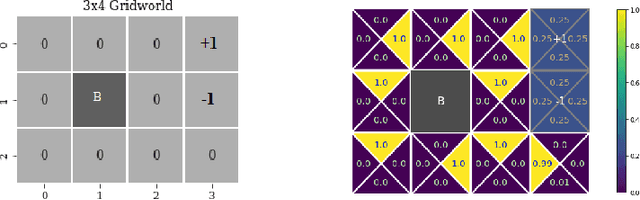
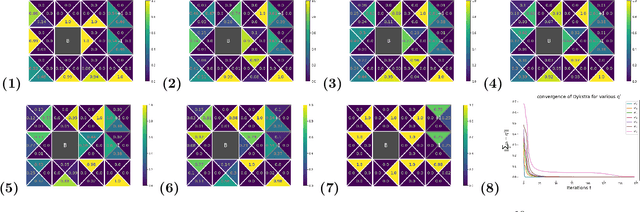
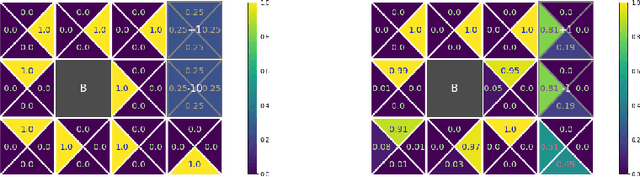
Distributionally-Constrained Policy Optimization via Unbalanced Optimal Transport

We consider constrained policy optimization in Reinforcement Learning, where the constraints are in form of marginals on state visitations and global action executions. Given these distributions, we formulate policy optimization as unbalanced optimal transport over the space of occupancy measures. We propose a general purpose RL objective based on Bregman divergence and optimize it using Dykstra's algorithm. The approach admits an actor-critic algorithm for when the state or action space is large, and only samples from the marginals are available. We discuss applications of our approach and provide demonstrations to show the effectiveness of our algorithm.

Sequential Cooperative Bayesian Inference

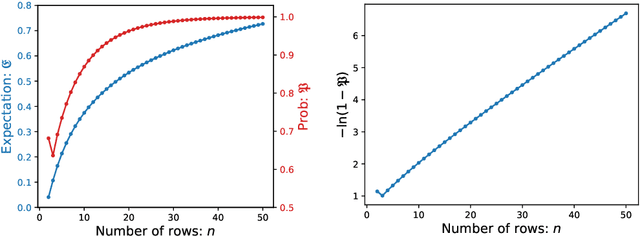
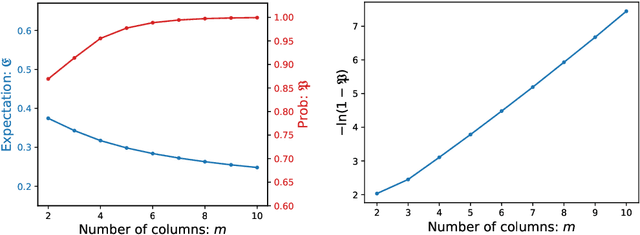
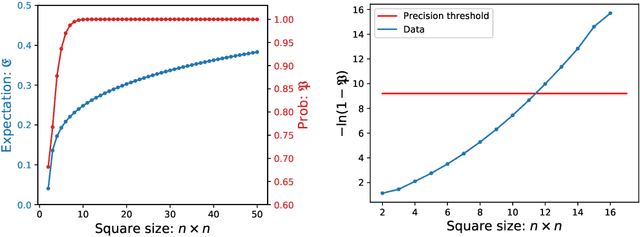
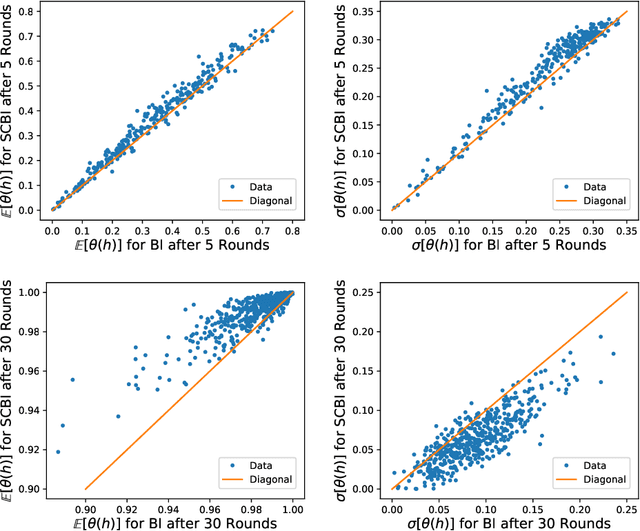
Cooperation is often implicitly assumed when learning from other agents. Cooperation implies that the agent selecting the data, and the agent learning from the data, have the same goal, that the learner infer the intended hypothesis. Recent models in human and machine learning have demonstrated the possibility of cooperation. We seek foundational theoretical results for cooperative inference by Bayesian agents through sequential data. We develop novel approaches analyzing consistency, rate of convergence and stability of Sequential Cooperative Bayesian Inference (SCBI). Our analysis of the effectiveness, sample efficiency and robustness show that cooperation is not only possible in specific instances but theoretically well-founded in general. We discuss implications for human-human and human-machine cooperation.

A mathematical theory of cooperative communication

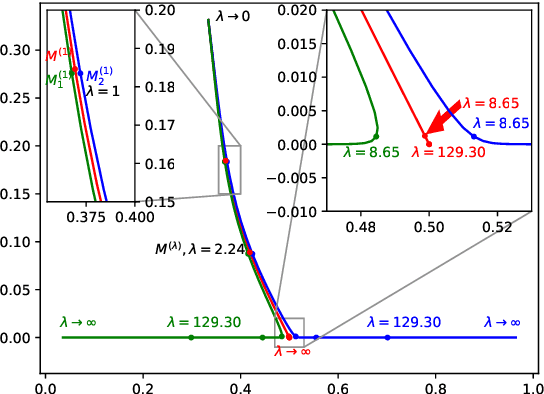
Cooperative communication plays a central role in theories of human cognition, language, development, and culture, and is increasingly relevant in human-algorithm and robot interaction. Existing models are algorithmic in nature and do not shed light on the statistical problem solved in cooperation or on constraints imposed by violations of common ground. We present a mathematical theory of cooperative communication that unifies three broad classes of algorithmic models as approximations of Optimal Transport (OT). We derive a statistical interpretation for the problem approximated by existing models in terms of entropy minimization, or likelihood maximizing, plans. We show that some models are provably robust to violations of common ground, even supporting online, approximate recovery from discovered violations, and derive conditions under which other models are provably not robust. We do so using gradient-based methods which introduce novel algorithmic-level perspectives on cooperative communication. Our mathematical approach complements and extends empirical research, providing strong theoretical tools derivation of a priori constraints on models and implications for cooperative communication in theory and practice.