Evolution of beliefs in social networks

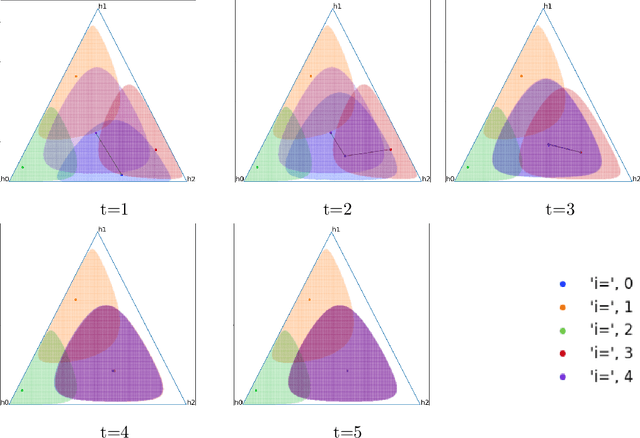
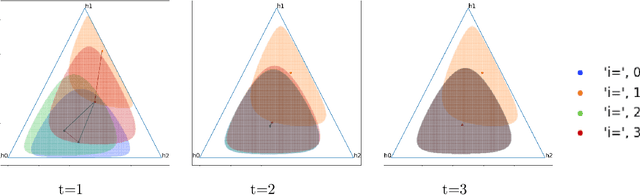
Evolution of beliefs of a society are a product of interactions between people (horizontal transmission) in the society over generations (vertical transmission). Researchers have studied both horizontal and vertical transmission separately. Extending prior work, we propose a new theoretical framework which allows application of tools from Markov chain theory to the analysis of belief evolution via horizontal and vertical transmission. We analyze three cases: static network, randomly changing network, and homophily-based dynamic network. Whereas the former two assume network structure is independent of beliefs, the latter assumes that people tend to communicate with those who have similar beliefs. We prove under general conditions that both static and randomly changing networks converge to a single set of beliefs among all individuals along with the rate of convergence. We prove that homophily-based network structures do not in general converge to a single set of beliefs shared by all and prove lower bounds on the number of different limiting beliefs as a function of initial beliefs. We conclude by discussing implications for prior theories and directions for future work.

A mathematical theory of cooperative communication

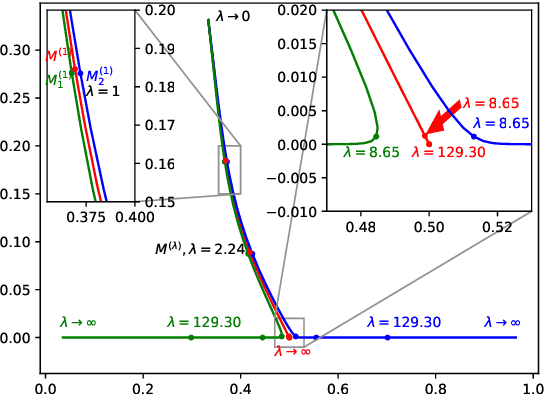
Cooperative communication plays a central role in theories of human cognition, language, development, and culture, and is increasingly relevant in human-algorithm and robot interaction. Existing models are algorithmic in nature and do not shed light on the statistical problem solved in cooperation or on constraints imposed by violations of common ground. We present a mathematical theory of cooperative communication that unifies three broad classes of algorithmic models as approximations of Optimal Transport (OT). We derive a statistical interpretation for the problem approximated by existing models in terms of entropy minimization, or likelihood maximizing, plans. We show that some models are provably robust to violations of common ground, even supporting online, approximate recovery from discovered violations, and derive conditions under which other models are provably not robust. We do so using gradient-based methods which introduce novel algorithmic-level perspectives on cooperative communication. Our mathematical approach complements and extends empirical research, providing strong theoretical tools derivation of a priori constraints on models and implications for cooperative communication in theory and practice.