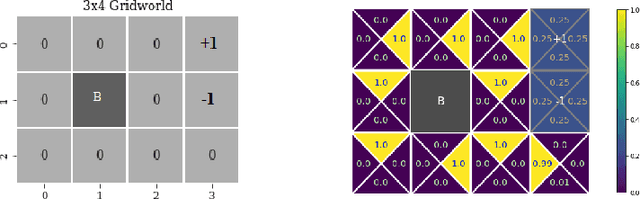
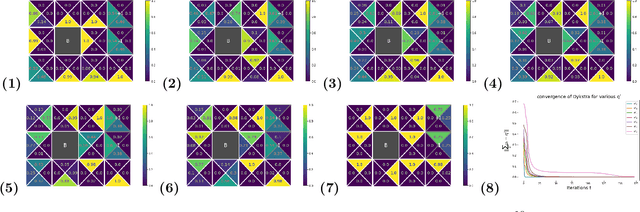
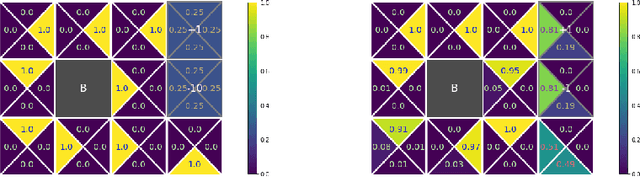
Distributionally-Constrained Policy Optimization via Unbalanced Optimal Transport

We consider constrained policy optimization in Reinforcement Learning, where the constraints are in form of marginals on state visitations and global action executions. Given these distributions, we formulate policy optimization as unbalanced optimal transport over the space of occupancy measures. We propose a general purpose RL objective based on Bregman divergence and optimize it using Dykstra's algorithm. The approach admits an actor-critic algorithm for when the state or action space is large, and only samples from the marginals are available. We discuss applications of our approach and provide demonstrations to show the effectiveness of our algorithm.

Manifold learning from a teacher's demonstrations

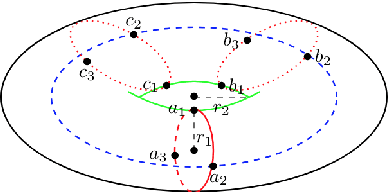
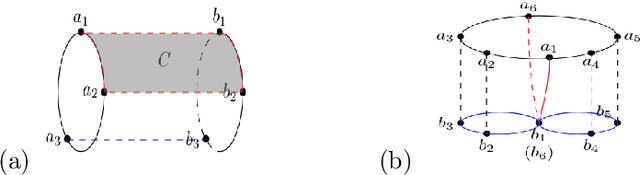
We consider the problem of manifold learning. Extending existing approaches of learning from randomly sampled data points, we consider contexts where data may be chosen by a teacher. We analyze learning from teachers who can provide structured data such as points, comparisons (pairs of points), demonstrations (sequences). We prove results showing that the former two do not yield notable decreases in the amount of data required to infer a manifold. Teaching by demonstration can yield remarkable decreases in the amount of data required, if we allow the goal to be teaching up to topology. We further analyze teaching learners in the context of persistence homology. Teaching topology can greatly reduce the number of datapoints required to infer correct geometry, and allows learning from teachers who themselves do not have full knowledge of the true manifold. We conclude with implications for learning in humans and machines.

Optimal Cooperative Inference

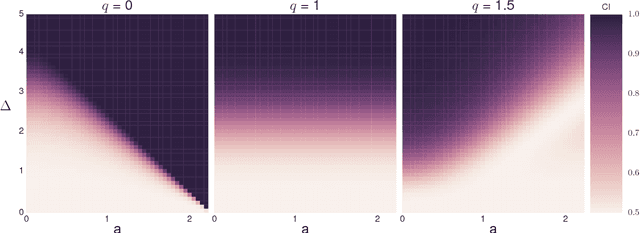
Cooperative transmission of data fosters rapid accumulation of knowledge by efficiently combining experiences across learners. Although well studied in human learning and increasingly in machine learning, we lack formal frameworks through which we may reason about the benefits and limitations of cooperative inference. We present such a framework. We introduce novel indices for measuring the effectiveness of probabilistic and cooperative information transmission. We relate our indices to the well-known Teaching Dimension in deterministic settings. We prove conditions under which optimal cooperative inference can be achieved, including a representation theorem that constrains the form of inductive biases for learners optimized for cooperative inference. We conclude by demonstrating how these principles may inform the design of machine learning algorithms and discuss implications for human and machine learning.