Structured Evaluation of Synthetic Tabular Data

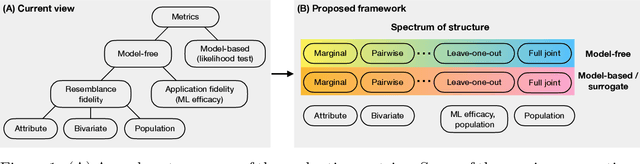
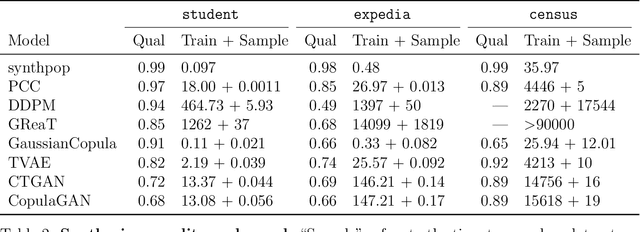
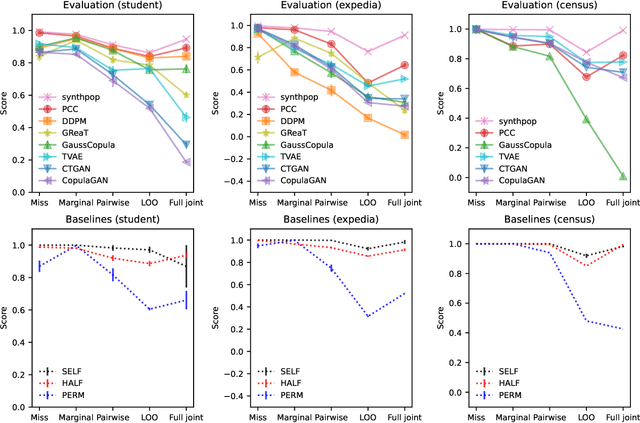
Tabular data is common yet typically incomplete, small in volume, and access-restricted due to privacy concerns. Synthetic data generation offers potential solutions. Many metrics exist for evaluating the quality of synthetic tabular data; however, we lack an objective, coherent interpretation of the many metrics. To address this issue, we propose an evaluation framework with a single, mathematical objective that posits that the synthetic data should be drawn from the same distribution as the observed data. Through various structural decomposition of the objective, this framework allows us to reason for the first time the completeness of any set of metrics, as well as unifies existing metrics, including those that stem from fidelity considerations, downstream application, and model-based approaches. Moreover, the framework motivates model-free baselines and a new spectrum of metrics. We evaluate structurally informed synthesizers and synthesizers powered by deep learning. Using our structured framework, we show that synthetic data generators that explicitly represent tabular structure outperform other methods, especially on smaller datasets.

A psychological theory of explainability

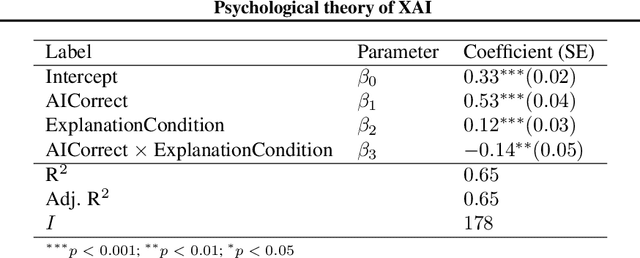
The goal of explainable Artificial Intelligence (XAI) is to generate human-interpretable explanations, but there are no computationally precise theories of how humans interpret AI generated explanations. The lack of theory means that validation of XAI must be done empirically, on a case-by-case basis, which prevents systematic theory-building in XAI. We propose a psychological theory of how humans draw conclusions from saliency maps, the most common form of XAI explanation, which for the first time allows for precise prediction of explainee inference conditioned on explanation. Our theory posits that absent explanation humans expect the AI to make similar decisions to themselves, and that they interpret an explanation by comparison to the explanations they themselves would give. Comparison is formalized via Shepard's universal law of generalization in a similarity space, a classic theory from cognitive science. A pre-registered user study on AI image classifications with saliency map explanations demonstrate that our theory quantitatively matches participants' predictions of the AI.

Explainable AI for Natural Adversarial Images

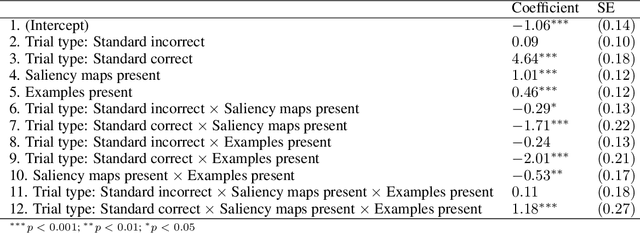
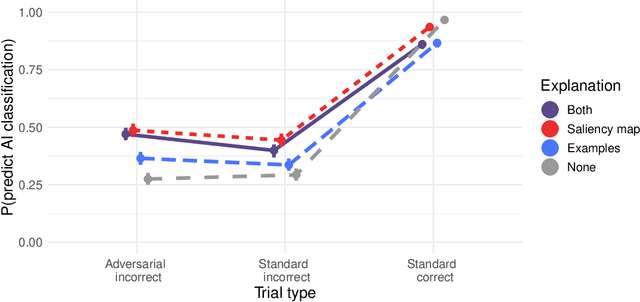
Adversarial images highlight how vulnerable modern image classifiers are to perturbations outside of their training set. Human oversight might mitigate this weakness, but depends on humans understanding the AI well enough to predict when it is likely to make a mistake. In previous work we have found that humans tend to assume that the AI's decision process mirrors their own. Here we evaluate if methods from explainable AI can disrupt this assumption to help participants predict AI classifications for adversarial and standard images. We find that both saliency maps and examples facilitate catching AI errors, but their effects are not additive, and saliency maps are more effective than examples.

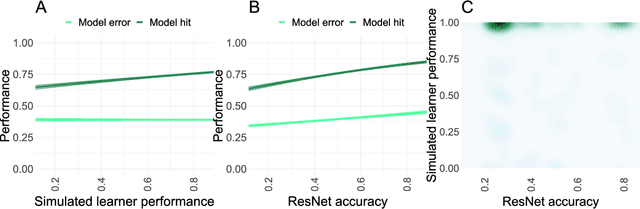
Explainable AI for medical imaging: Explaining pneumothorax diagnoses with Bayesian Teaching

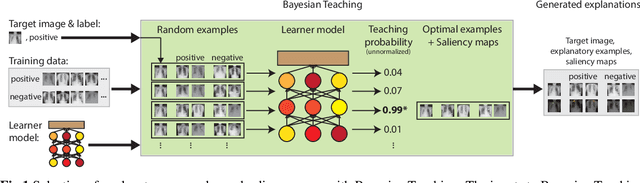
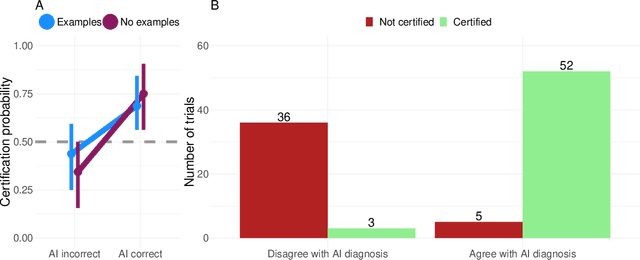
Limited expert time is a key bottleneck in medical imaging. Due to advances in image classification, AI can now serve as decision-support for medical experts, with the potential for great gains in radiologist productivity and, by extension, public health. However, these gains are contingent on building and maintaining experts' trust in the AI agents. Explainable AI may build such trust by helping medical experts to understand the AI decision processes behind diagnostic judgements. Here we introduce and evaluate explanations based on Bayesian Teaching, a formal account of explanation rooted in the cognitive science of human learning. We find that medical experts exposed to explanations generated by Bayesian Teaching successfully predict the AI's diagnostic decisions and are more likely to certify the AI for cases when the AI is correct than when it is wrong, indicating appropriate trust. These results show that Explainable AI can be used to support human-AI collaboration in medical imaging.

Abstraction, Validation, and Generalization for Explainable Artificial Intelligence

Neural network architectures are achieving superhuman performance on an expanding range of tasks. To effectively and safely deploy these systems, their decision-making must be understandable to a wide range of stakeholders. Methods to explain AI have been proposed to answer this challenge, but a lack of theory impedes the development of systematic abstractions which are necessary for cumulative knowledge gains. We propose Bayesian Teaching as a framework for unifying explainable AI (XAI) by integrating machine learning and human learning. Bayesian Teaching formalizes explanation as a communication act of an explainer to shift the beliefs of an explainee. This formalization decomposes any XAI method into four components: (1) the inference to be explained, (2) the explanatory medium, (3) the explainee model, and (4) the explainer model. The abstraction afforded by Bayesian Teaching to decompose any XAI method elucidates the invariances among them. The decomposition of XAI systems enables modular validation, as each of the first three components listed can be tested semi-independently. This decomposition also promotes generalization through recombination of components from different XAI systems, which facilitates the generation of novel variants. These new variants need not be evaluated one by one provided that each component has been validated, leading to an exponential decrease in development time. Finally, by making the goal of explanation explicit, Bayesian Teaching helps developers to assess how suitable an XAI system is for its intended real-world use case. Thus, Bayesian Teaching provides a theoretical framework that encourages systematic, scientific investigation of XAI.

Mitigating belief projection in explainable artificial intelligence via Bayesian Teaching

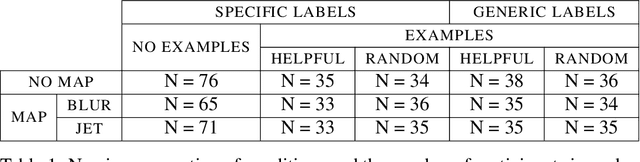
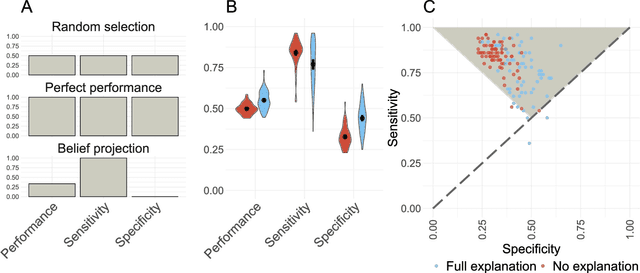
State-of-the-art deep-learning systems use decision rules that are challenging for humans to model. Explainable AI (XAI) attempts to improve human understanding but rarely accounts for how people typically reason about unfamiliar agents. We propose explicitly modeling the human explainee via Bayesian Teaching, which evaluates explanations by how much they shift explainees' inferences toward a desired goal. We assess Bayesian Teaching in a binary image classification task across a variety of contexts. Absent intervention, participants predict that the AI's classifications will match their own, but explanations generated by Bayesian Teaching improve their ability to predict the AI's judgements by moving them away from this prior belief. Bayesian Teaching further allows each case to be broken down into sub-examples (here saliency maps). These sub-examples complement whole examples by improving error detection for familiar categories, whereas whole examples help predict correct AI judgements of unfamiliar cases.

Interpretable deep Gaussian processes

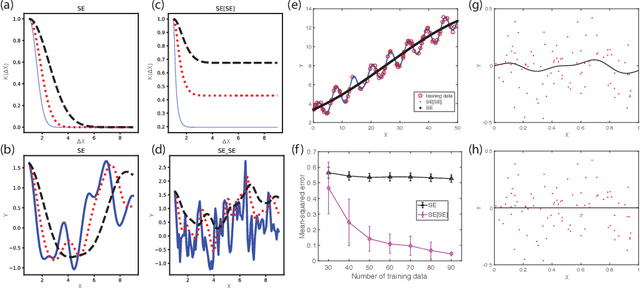
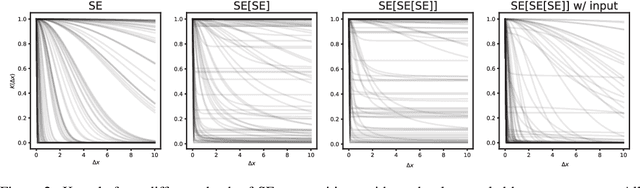
We propose interpretable deep Gaussian Processes (GPs) that combine the expressiveness of deep Neural Networks (NNs) with quantified uncertainty of deep GPs. Our approach is based on approximating deep GP as a GP, which allows explicit, analytic forms for compositions of a wide variety of kernels. Consequently, our approach admits interpretation as both NNs with specified activation functions and as a variational approximation to deep GPs. We provide general recipes for deriving the effective kernels for deep GPs of two, three, or infinitely many layers, composed of homogeneous or heterogeneous kernels. Results illustrate the expressiveness of our effective kernels through samples from the prior and inference on simulated data and demonstrate advantages of interpretability by analysis of analytic forms, drawing relations and equivalences across kernels, and a priori identification of non-pathological regimes of hyperparameter space.

Standing Wave Decomposition Gaussian Process

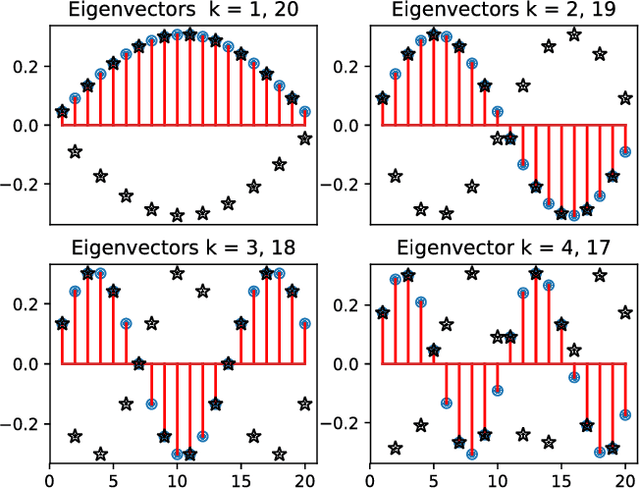
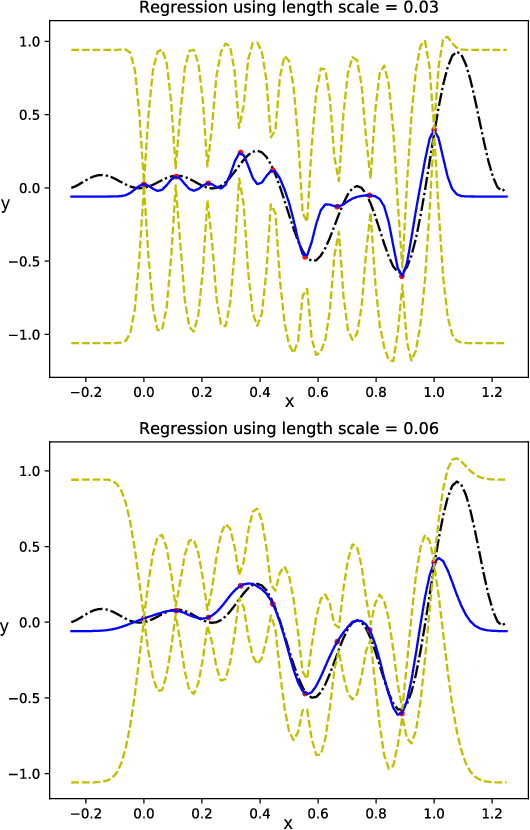
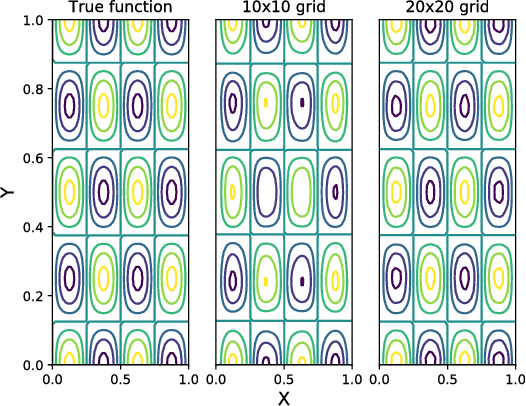
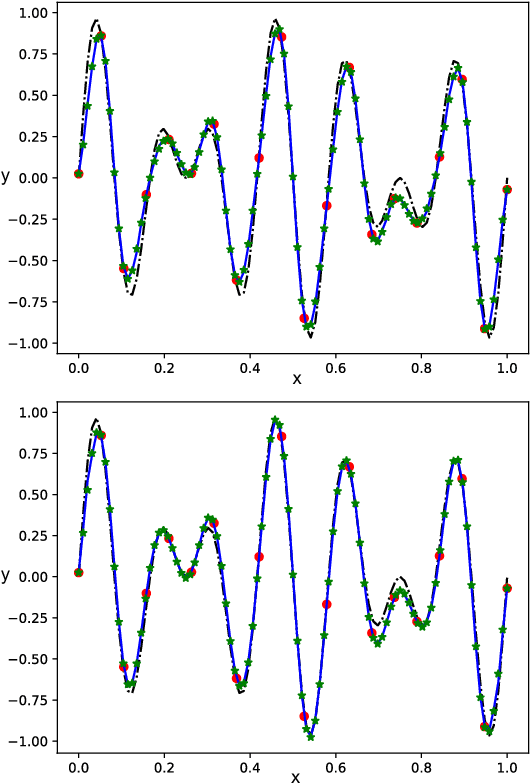
We propose a Standing Wave Decomposition (SWD) approximation to Gaussian Process regression (GP). GP involves a costly matrix inversion operation, which limits applicability to large data analysis. For an input space that can be approximated by a grid and when correlations among data are short-ranged, the kernel matrix inversion can be replaced by analytic diagonalization using the SWD. We show that this approach applies to uni- and multi-dimensional input data, extends to include longer-range correlations, and the grid can be in a latent space and used as inducing points. Through simulations, we show that our approximate method applied to the squared exponential kernel outperforms existing methods in predictive accuracy per unit time in the regime where data are plentiful. Our SWD-GP is recommended for regression analyses where there is a relatively large amount of data and/or there are constraints on computation time.

Optimal Cooperative Inference

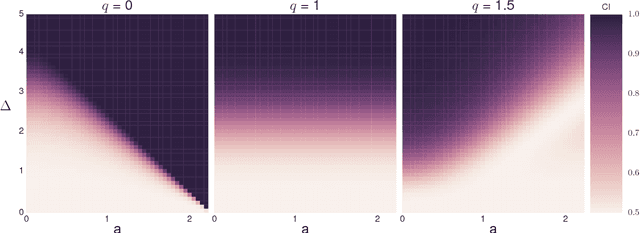
Cooperative transmission of data fosters rapid accumulation of knowledge by efficiently combining experiences across learners. Although well studied in human learning and increasingly in machine learning, we lack formal frameworks through which we may reason about the benefits and limitations of cooperative inference. We present such a framework. We introduce novel indices for measuring the effectiveness of probabilistic and cooperative information transmission. We relate our indices to the well-known Teaching Dimension in deterministic settings. We prove conditions under which optimal cooperative inference can be achieved, including a representation theorem that constrains the form of inductive biases for learners optimized for cooperative inference. We conclude by demonstrating how these principles may inform the design of machine learning algorithms and discuss implications for human and machine learning.