Bayesian inference with finitely wide neural networks

The analytic inference, e.g. predictive distribution being in closed form, may be an appealing benefit for machine learning practitioners when they treat wide neural networks as Gaussian process in Bayesian setting. The realistic widths, however, are finite and cause weak deviation from the Gaussianity under which partial marginalization of random variables in a model is straightforward. On the basis of multivariate Edgeworth expansion, we propose a non-Gaussian distribution in differential form to model a finite set of outputs from a random neural network, and derive the corresponding marginal and conditional properties. Thus, we are able to derive the non-Gaussian posterior distribution in Bayesian regression task. In addition, in the bottlenecked deep neural networks, a weight space representation of deep Gaussian process, the non-Gaussianity is investigated through the marginal kernel.

On Connecting Deep Trigonometric Networks with Deep Gaussian Processes: Covariance, Expressivity, and Neural Tangent Kernel

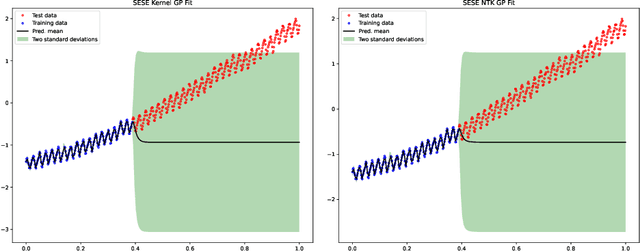
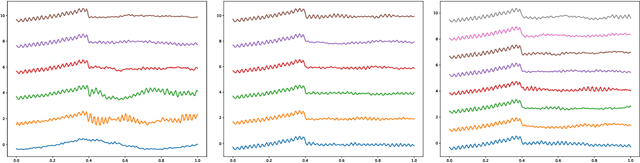
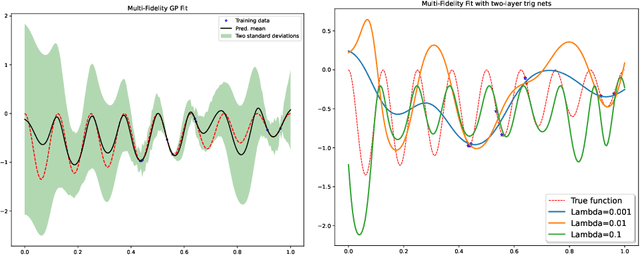
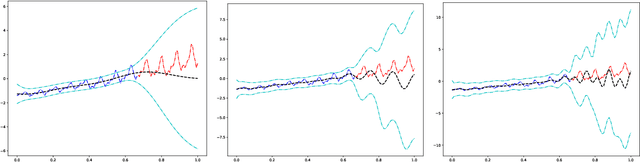
Deep Gaussian Process as a Bayesian learning model is promising because it is expressive and capable of uncertainty estimation. With Bochner's theorem, we can view the deep Gaussian process with squared exponential kernels as a deep trigonometric network consisting of the random feature layers, sine and cosine activation units, and random weight layers. Focusing on this particular class of models allows us to obtain analytical results. We shall show that the weight space view yields the same effective covariance functions which were obtained previously in function space. The heavy statistical tails can be studied with multivariate characteristic function. In addition, the trig networks are flexible and expressive as one can freely adopt different prior distributions over the parameters in weight and feature layers. Lastly, the deep trigonometric network representation of deep Gaussian process allows the derivation of its neural tangent kernel, which can reveal the mean of predictive distribution from the intractable inference.

Conditional Deep Gaussian Processes: empirical Bayes hyperdata learning

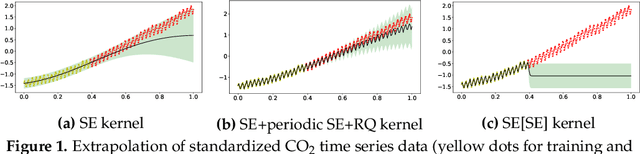
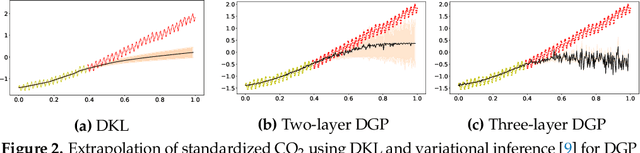
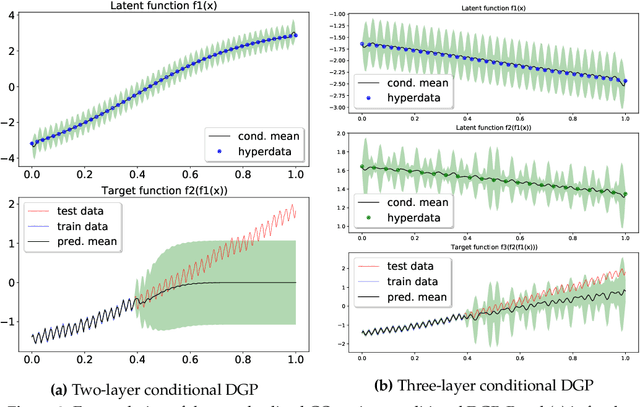
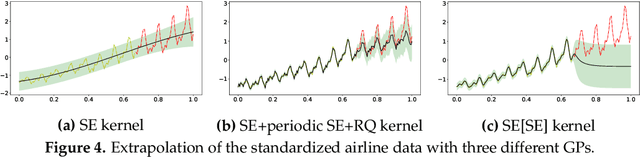
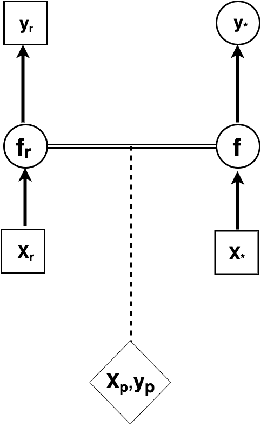
It is desirable to combine the expressive power of deep learning with Gaussian Process (GP) in one expressive Bayesian learning model. Deep kernel learning proposed in [1] showed success in adopting a deep network for feature extraction followed by a GP used as function model. Recently, [2] suggested that the deterministic nature of feature extractor may lead to overfitting while the replacement with a Bayesian network seemed to cure it. Here, we propose the conditional Deep Gaussian Process (DGP) in which the intermediate GPs in hierarchical composition are supported by the hyperdata and the exposed GP remains zero mean. Motivated by the inducing points in sparse GP, the hyperdata also play the role of function supports, but are hyperparameters rather than random variables. We use the moment matching method [3] to approximate the marginal prior for conditional DGP with a GP carrying an effective kernel. Thus, as in empirical Bayes, the hyperdata are learned by optimizing the approximate marginal likelihood which implicitly depends on the hyperdata via the kernel. We shall show the equivalence with the deep kernel learning in the limit of dense hyperdata in latent space. However, the conditional DGP and the corresponding approximate inference enjoy the benefit of being more Bayesian than deep kernel learning. Preliminary extrapolation results demonstrate expressive power of the proposed model compared with GP kernel composition, DGP variational inference, and deep kernel learning. We also address the non-Gaussian aspect of our model as well as way of upgrading to a full Bayes inference.

Multi-source Deep Gaussian Process Kernel Learning

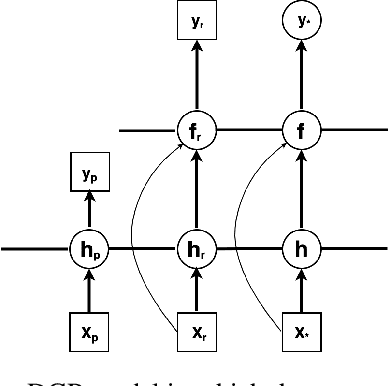
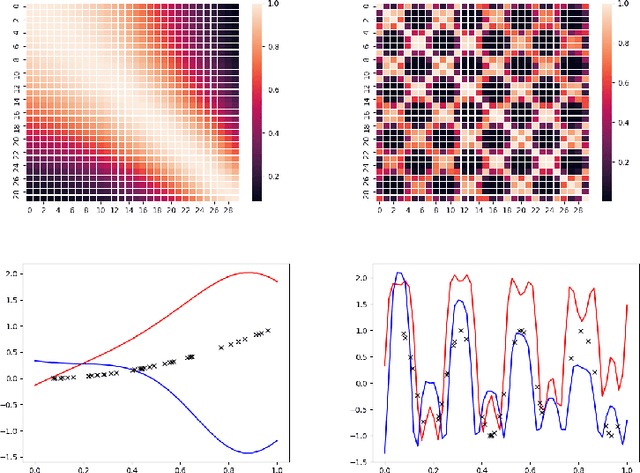
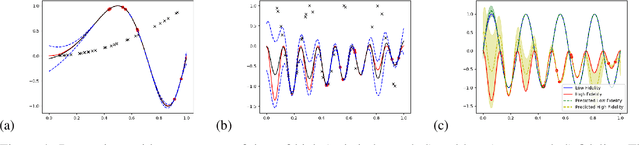
For many problems, relevant data are plentiful but explicit knowledge is not. Predictions about target variables may be informed by data sources that are noisy but plentiful, or data which the target variable is merely some function of. Intrepretable and flexible machine learning methods capable of fusing data across sources are lacking. We generalize the Deep Gaussian Processes so that GPs in intermediate layers can represent the posterior distribution summarizing the data from a related source. We model the prior-posterior stacking DGP with a single GP. The exact second moment of DGP is calculated analytically, and is taken as the kernel function for GP. The result is a kernel that captures effective correlation through function composition, reflects the structure of the observations from other data sources, and can be used to inform prediction based on limited direct observations. Therefore, the approximation of prior-posterior DGP can be considered a novel kernel composition which blends the kernels in different layers and have explicit dependence on the data. We consider two synthetic multi-source prediction problems: a) predicting a target variable that is merely a function of the source data and b) predicting noise-free data using a kernel trained on noisy data. Our method produces better prediction and tighter uncertainty on the synthetic data when comparing with standard GP and other DGP method, suggesting that our data-informed approximate DGPs are a powerful tool for integrating data across sources.

Interpretable deep Gaussian processes

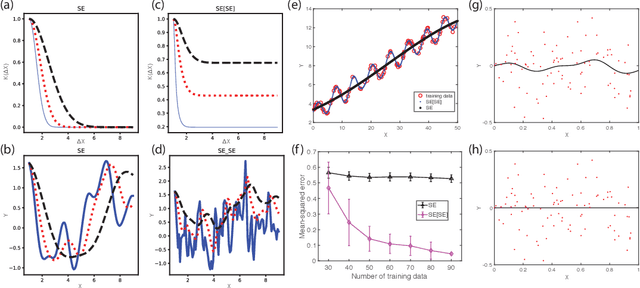
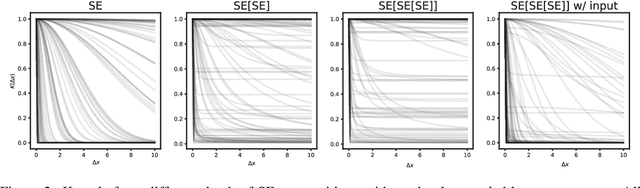
We propose interpretable deep Gaussian Processes (GPs) that combine the expressiveness of deep Neural Networks (NNs) with quantified uncertainty of deep GPs. Our approach is based on approximating deep GP as a GP, which allows explicit, analytic forms for compositions of a wide variety of kernels. Consequently, our approach admits interpretation as both NNs with specified activation functions and as a variational approximation to deep GPs. We provide general recipes for deriving the effective kernels for deep GPs of two, three, or infinitely many layers, composed of homogeneous or heterogeneous kernels. Results illustrate the expressiveness of our effective kernels through samples from the prior and inference on simulated data and demonstrate advantages of interpretability by analysis of analytic forms, drawing relations and equivalences across kernels, and a priori identification of non-pathological regimes of hyperparameter space.

Standing Wave Decomposition Gaussian Process

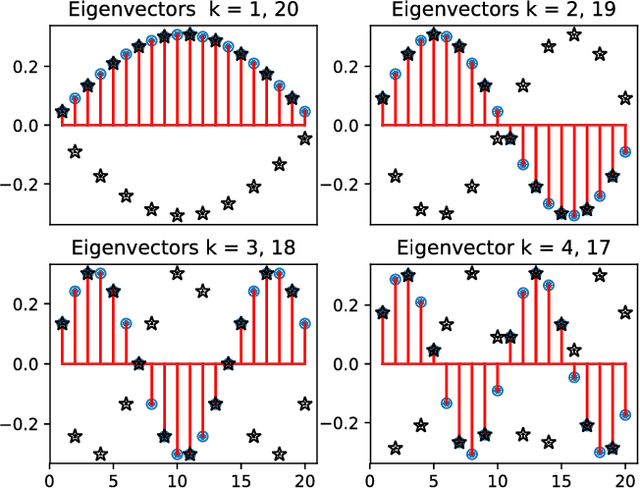
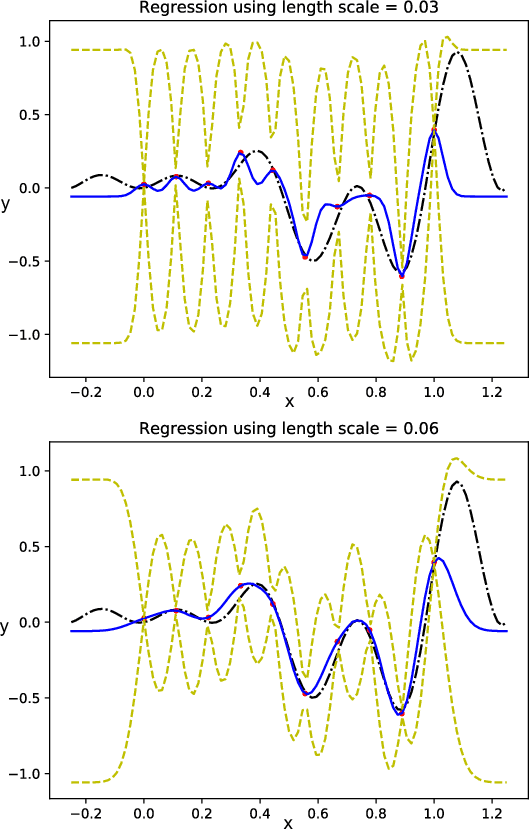
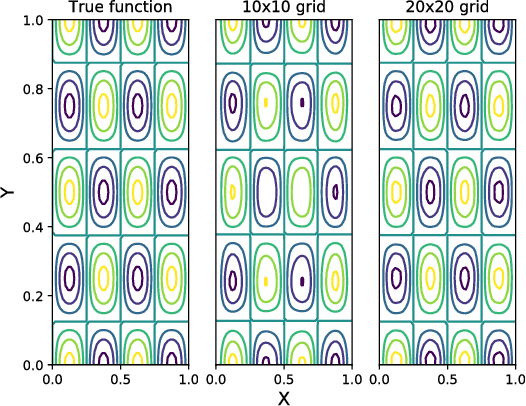
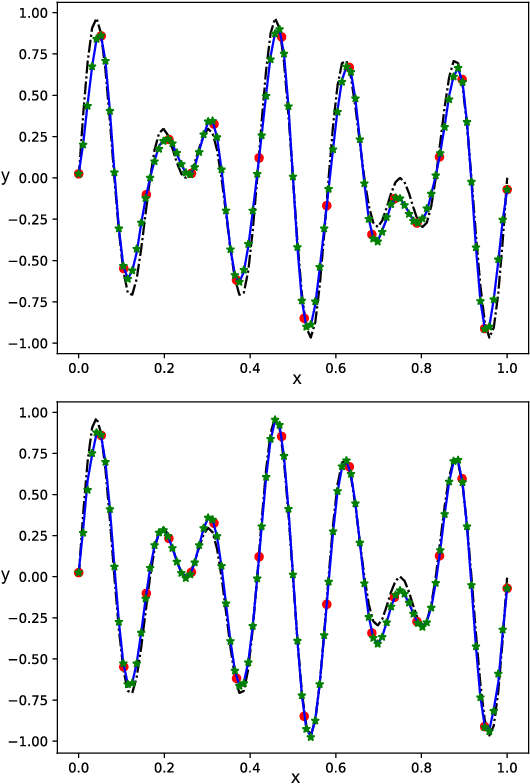
We propose a Standing Wave Decomposition (SWD) approximation to Gaussian Process regression (GP). GP involves a costly matrix inversion operation, which limits applicability to large data analysis. For an input space that can be approximated by a grid and when correlations among data are short-ranged, the kernel matrix inversion can be replaced by analytic diagonalization using the SWD. We show that this approach applies to uni- and multi-dimensional input data, extends to include longer-range correlations, and the grid can be in a latent space and used as inducing points. Through simulations, we show that our approximate method applied to the squared exponential kernel outperforms existing methods in predictive accuracy per unit time in the regime where data are plentiful. Our SWD-GP is recommended for regression analyses where there is a relatively large amount of data and/or there are constraints on computation time.