Interpretable deep Gaussian processes
Paper and Code
May 27, 2019
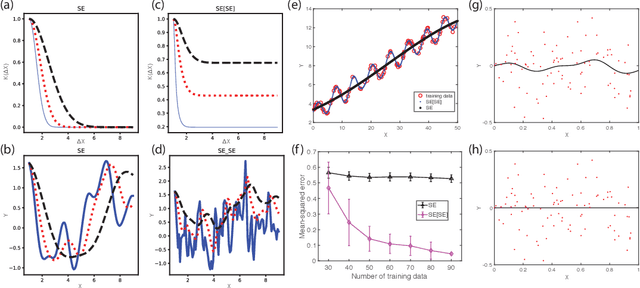

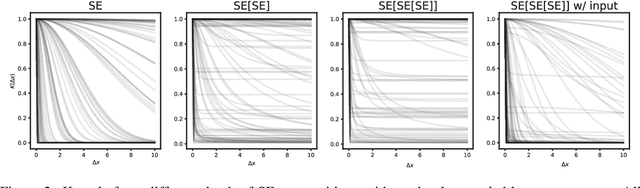
We propose interpretable deep Gaussian Processes (GPs) that combine the expressiveness of deep Neural Networks (NNs) with quantified uncertainty of deep GPs. Our approach is based on approximating deep GP as a GP, which allows explicit, analytic forms for compositions of a wide variety of kernels. Consequently, our approach admits interpretation as both NNs with specified activation functions and as a variational approximation to deep GPs. We provide general recipes for deriving the effective kernels for deep GPs of two, three, or infinitely many layers, composed of homogeneous or heterogeneous kernels. Results illustrate the expressiveness of our effective kernels through samples from the prior and inference on simulated data and demonstrate advantages of interpretability by analysis of analytic forms, drawing relations and equivalences across kernels, and a priori identification of non-pathological regimes of hyperparameter space.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge