Coupled Variational Autoencoder

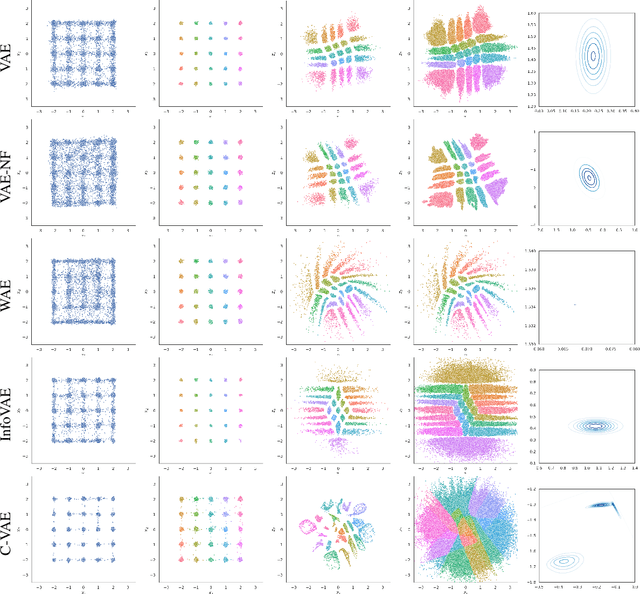
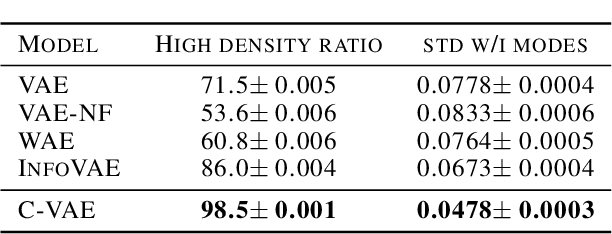
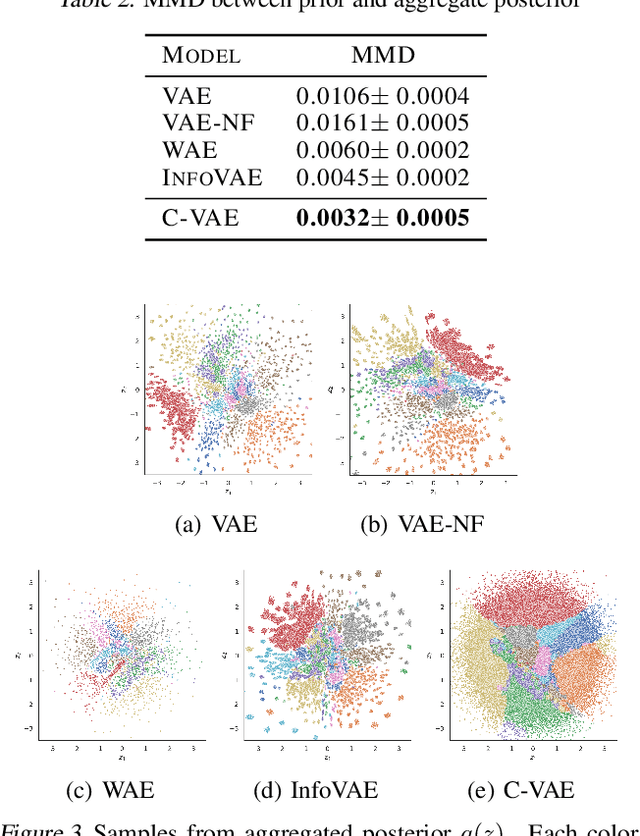
Variational auto-encoders are powerful probabilistic models in generative tasks but suffer from generating low-quality samples which are caused by the holes in the prior. We propose the Coupled Variational Auto-Encoder (C-VAE), which formulates the VAE problem as one of Optimal Transport (OT) between the prior and data distributions. The C-VAE allows greater flexibility in priors and natural resolution of the prior hole problem by enforcing coupling between the prior and the data distribution and enables flexible optimization through the primal, dual, and semi-dual formulations of entropic OT. Simulations on synthetic and real data show that the C-VAE outperforms alternatives including VAE, WAE, and InfoVAE in fidelity to the data, quality of the latent representation, and in quality of generated samples.

Interpretable deep Gaussian processes

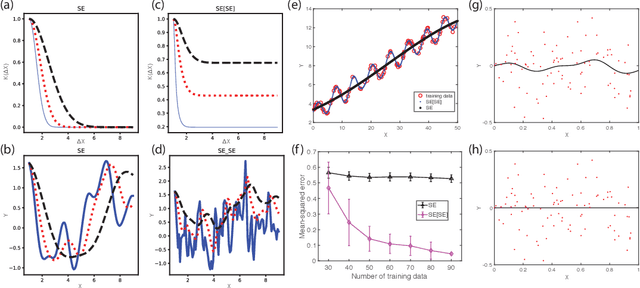
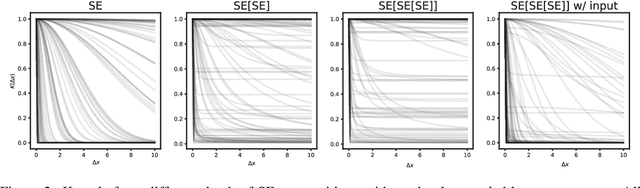
We propose interpretable deep Gaussian Processes (GPs) that combine the expressiveness of deep Neural Networks (NNs) with quantified uncertainty of deep GPs. Our approach is based on approximating deep GP as a GP, which allows explicit, analytic forms for compositions of a wide variety of kernels. Consequently, our approach admits interpretation as both NNs with specified activation functions and as a variational approximation to deep GPs. We provide general recipes for deriving the effective kernels for deep GPs of two, three, or infinitely many layers, composed of homogeneous or heterogeneous kernels. Results illustrate the expressiveness of our effective kernels through samples from the prior and inference on simulated data and demonstrate advantages of interpretability by analysis of analytic forms, drawing relations and equivalences across kernels, and a priori identification of non-pathological regimes of hyperparameter space.