On Connecting Deep Trigonometric Networks with Deep Gaussian Processes: Covariance, Expressivity, and Neural Tangent Kernel

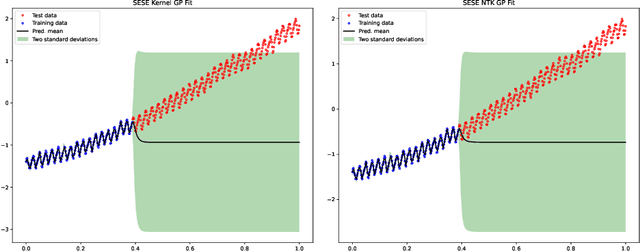
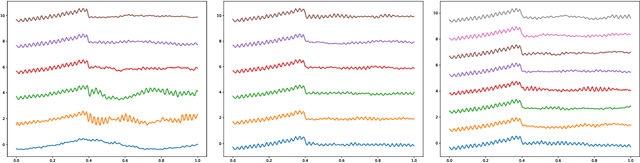
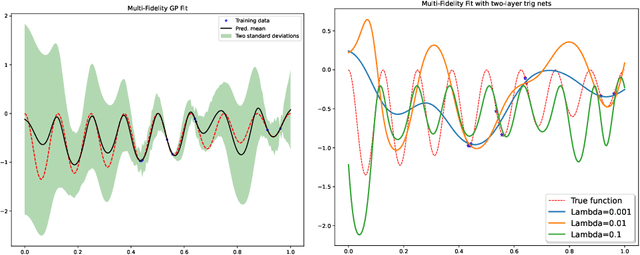
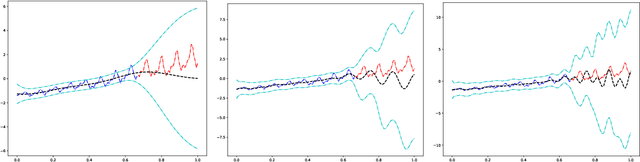
Deep Gaussian Process as a Bayesian learning model is promising because it is expressive and capable of uncertainty estimation. With Bochner's theorem, we can view the deep Gaussian process with squared exponential kernels as a deep trigonometric network consisting of the random feature layers, sine and cosine activation units, and random weight layers. Focusing on this particular class of models allows us to obtain analytical results. We shall show that the weight space view yields the same effective covariance functions which were obtained previously in function space. The heavy statistical tails can be studied with multivariate characteristic function. In addition, the trig networks are flexible and expressive as one can freely adopt different prior distributions over the parameters in weight and feature layers. Lastly, the deep trigonometric network representation of deep Gaussian process allows the derivation of its neural tangent kernel, which can reveal the mean of predictive distribution from the intractable inference.