Standing Wave Decomposition Gaussian Process
Paper and Code
Sep 17, 2018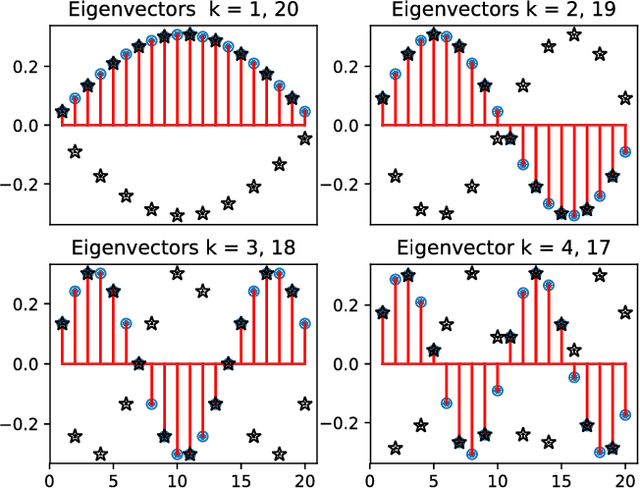
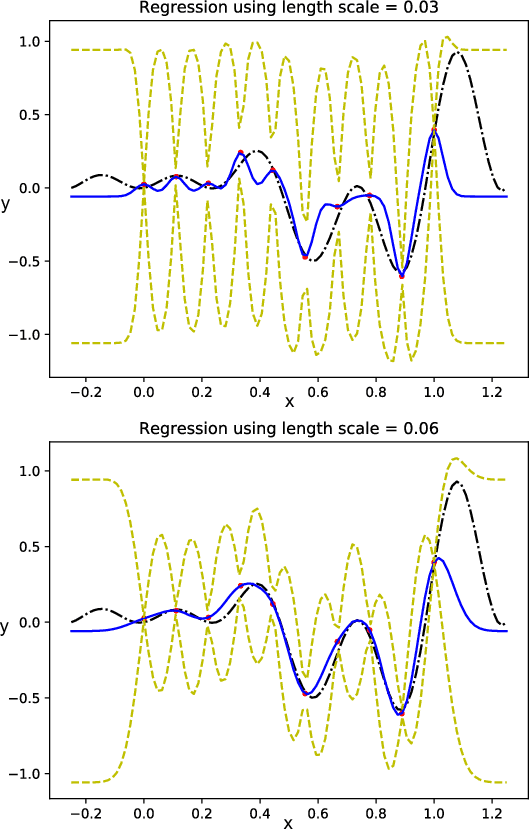
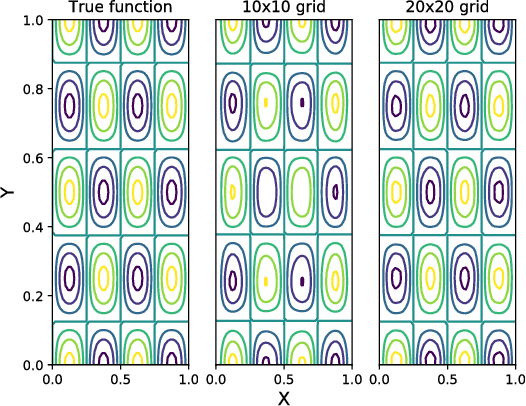
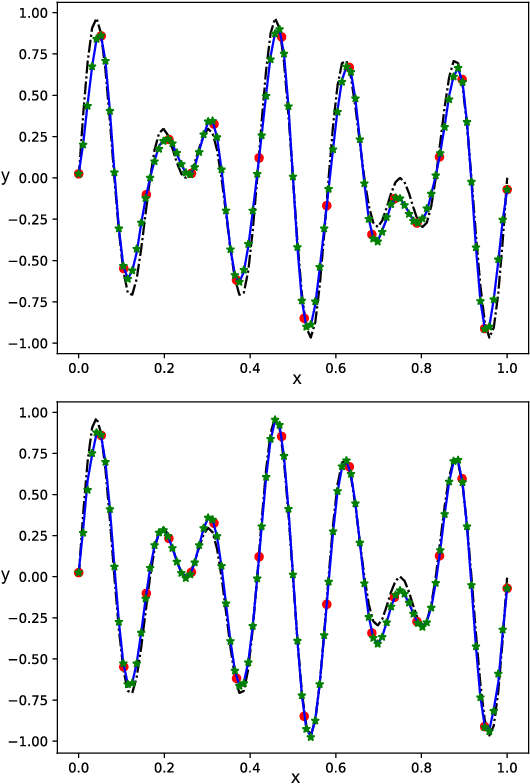
We propose a Standing Wave Decomposition (SWD) approximation to Gaussian Process regression (GP). GP involves a costly matrix inversion operation, which limits applicability to large data analysis. For an input space that can be approximated by a grid and when correlations among data are short-ranged, the kernel matrix inversion can be replaced by analytic diagonalization using the SWD. We show that this approach applies to uni- and multi-dimensional input data, extends to include longer-range correlations, and the grid can be in a latent space and used as inducing points. Through simulations, we show that our approximate method applied to the squared exponential kernel outperforms existing methods in predictive accuracy per unit time in the regime where data are plentiful. Our SWD-GP is recommended for regression analyses where there is a relatively large amount of data and/or there are constraints on computation time.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge