Conditional Deep Gaussian Processes: empirical Bayes hyperdata learning
Paper and Code
Oct 01, 2021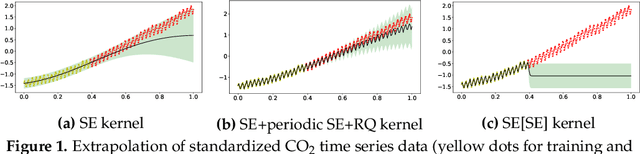
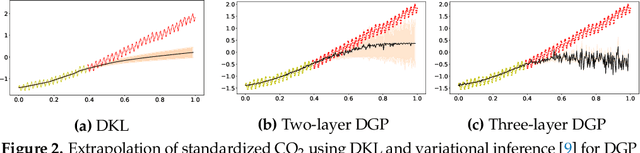
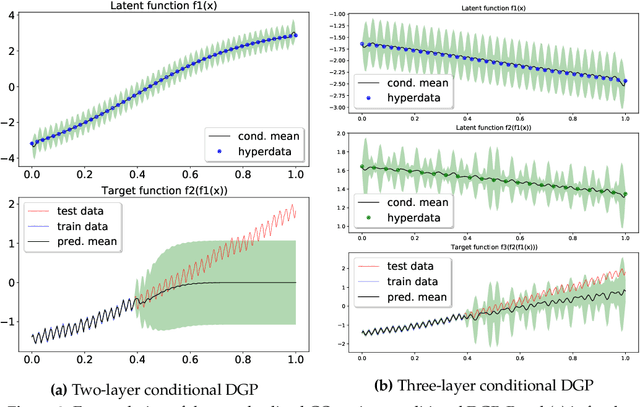
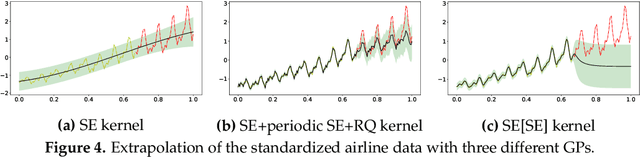
It is desirable to combine the expressive power of deep learning with Gaussian Process (GP) in one expressive Bayesian learning model. Deep kernel learning proposed in [1] showed success in adopting a deep network for feature extraction followed by a GP used as function model. Recently, [2] suggested that the deterministic nature of feature extractor may lead to overfitting while the replacement with a Bayesian network seemed to cure it. Here, we propose the conditional Deep Gaussian Process (DGP) in which the intermediate GPs in hierarchical composition are supported by the hyperdata and the exposed GP remains zero mean. Motivated by the inducing points in sparse GP, the hyperdata also play the role of function supports, but are hyperparameters rather than random variables. We use the moment matching method [3] to approximate the marginal prior for conditional DGP with a GP carrying an effective kernel. Thus, as in empirical Bayes, the hyperdata are learned by optimizing the approximate marginal likelihood which implicitly depends on the hyperdata via the kernel. We shall show the equivalence with the deep kernel learning in the limit of dense hyperdata in latent space. However, the conditional DGP and the corresponding approximate inference enjoy the benefit of being more Bayesian than deep kernel learning. Preliminary extrapolation results demonstrate expressive power of the proposed model compared with GP kernel composition, DGP variational inference, and deep kernel learning. We also address the non-Gaussian aspect of our model as well as way of upgrading to a full Bayes inference.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge