Explainable AI for medical imaging: Explaining pneumothorax diagnoses with Bayesian Teaching

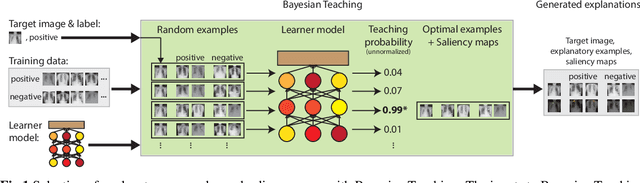
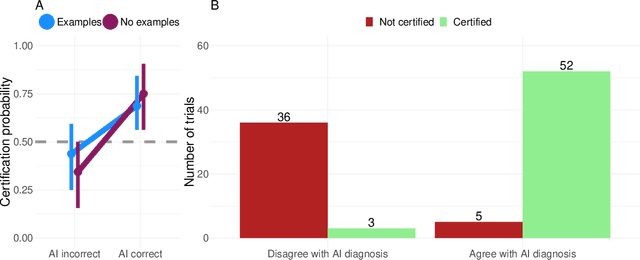
Limited expert time is a key bottleneck in medical imaging. Due to advances in image classification, AI can now serve as decision-support for medical experts, with the potential for great gains in radiologist productivity and, by extension, public health. However, these gains are contingent on building and maintaining experts' trust in the AI agents. Explainable AI may build such trust by helping medical experts to understand the AI decision processes behind diagnostic judgements. Here we introduce and evaluate explanations based on Bayesian Teaching, a formal account of explanation rooted in the cognitive science of human learning. We find that medical experts exposed to explanations generated by Bayesian Teaching successfully predict the AI's diagnostic decisions and are more likely to certify the AI for cases when the AI is correct than when it is wrong, indicating appropriate trust. These results show that Explainable AI can be used to support human-AI collaboration in medical imaging.

Batch Nonlinear Continuous-Time Trajectory Estimation as Exactly Sparse Gaussian Process Regression

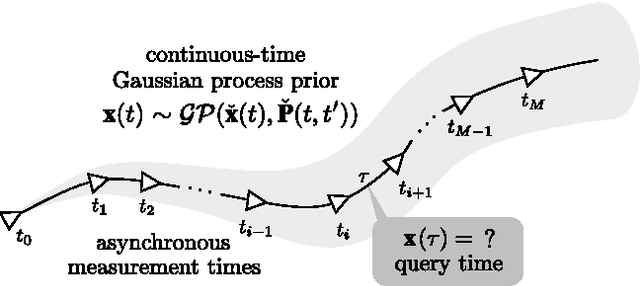
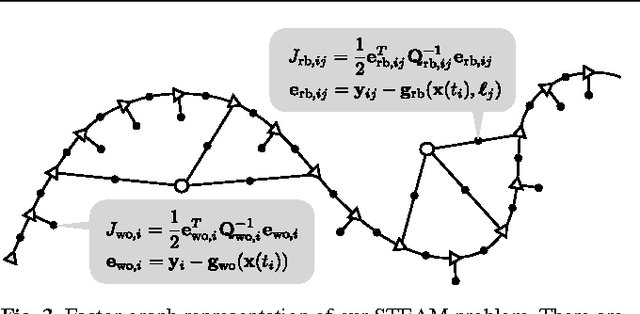
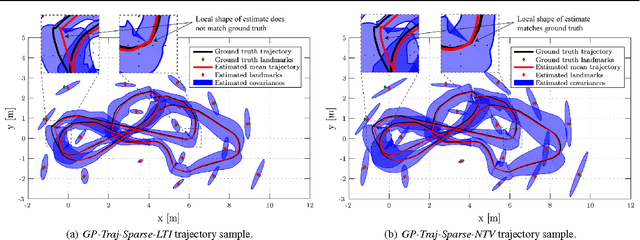
In this paper, we revisit batch state estimation through the lens of Gaussian process (GP) regression. We consider continuous-discrete estimation problems wherein a trajectory is viewed as a one-dimensional GP, with time as the independent variable. Our continuous-time prior can be defined by any nonlinear, time-varying stochastic differential equation driven by white noise; this allows the possibility of smoothing our trajectory estimates using a variety of vehicle dynamics models (e.g., `constant-velocity'). We show that this class of prior results in an inverse kernel matrix (i.e., covariance matrix between all pairs of measurement times) that is exactly sparse (block-tridiagonal) and that this can be exploited to carry out GP regression (and interpolation) very efficiently. When the prior is based on a linear, time-varying stochastic differential equation and the measurement model is also linear, this GP approach is equivalent to classical, discrete-time smoothing (at the measurement times); when a nonlinearity is present, we iterate over the whole trajectory to maximize accuracy. We test the approach experimentally on a simultaneous trajectory estimation and mapping problem using a mobile robot dataset.