Vote3Deep: Fast Object Detection in 3D Point Clouds Using Efficient Convolutional Neural Networks

This paper proposes a computationally efficient approach to detecting objects natively in 3D point clouds using convolutional neural networks (CNNs). In particular, this is achieved by leveraging a feature-centric voting scheme to implement novel convolutional layers which explicitly exploit the sparsity encountered in the input. To this end, we examine the trade-off between accuracy and speed for different architectures and additionally propose to use an L1 penalty on the filter activations to further encourage sparsity in the intermediate representations. To the best of our knowledge, this is the first work to propose sparse convolutional layers and L1 regularisation for efficient large-scale processing of 3D data. We demonstrate the efficacy of our approach on the KITTI object detection benchmark and show that Vote3Deep models with as few as three layers outperform the previous state of the art in both laser and laser-vision based approaches by margins of up to 40% while remaining highly competitive in terms of processing time.

Batch Nonlinear Continuous-Time Trajectory Estimation as Exactly Sparse Gaussian Process Regression

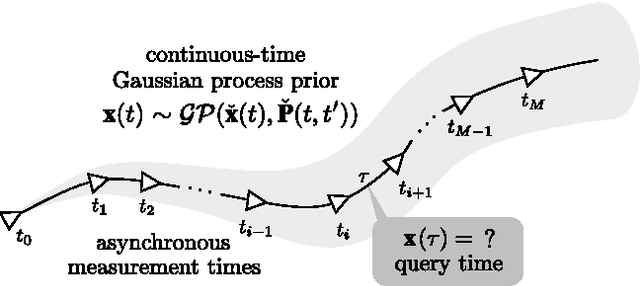
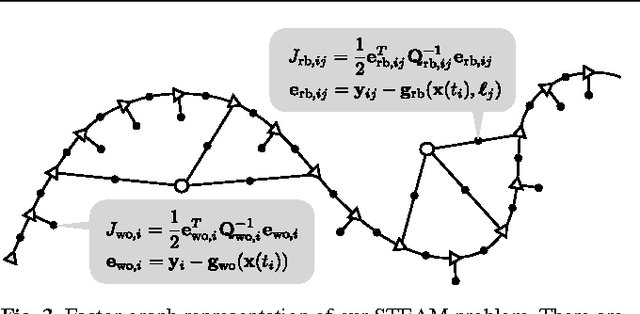
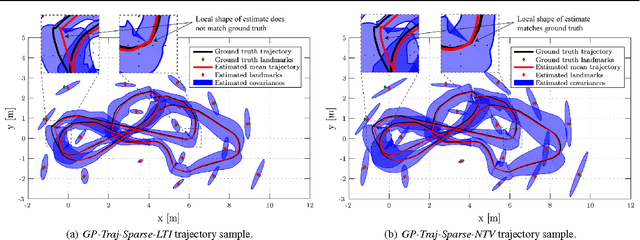
In this paper, we revisit batch state estimation through the lens of Gaussian process (GP) regression. We consider continuous-discrete estimation problems wherein a trajectory is viewed as a one-dimensional GP, with time as the independent variable. Our continuous-time prior can be defined by any nonlinear, time-varying stochastic differential equation driven by white noise; this allows the possibility of smoothing our trajectory estimates using a variety of vehicle dynamics models (e.g., `constant-velocity'). We show that this class of prior results in an inverse kernel matrix (i.e., covariance matrix between all pairs of measurement times) that is exactly sparse (block-tridiagonal) and that this can be exploited to carry out GP regression (and interpolation) very efficiently. When the prior is based on a linear, time-varying stochastic differential equation and the measurement model is also linear, this GP approach is equivalent to classical, discrete-time smoothing (at the measurement times); when a nonlinearity is present, we iterate over the whole trajectory to maximize accuracy. We test the approach experimentally on a simultaneous trajectory estimation and mapping problem using a mobile robot dataset.