Temporal parallelisation of continuous-time maximum-a-posteriori trajectory estimation

This paper proposes a parallel-in-time method for computing continuous-time maximum-a-posteriori (MAP) trajectory estimates of the states of partially observed stochastic differential equations (SDEs), with the goal of improving computational speed on parallel architectures. The MAP estimation problem is reformulated as a continuous-time optimal control problem based on the Onsager-Machlup functional. This reformulation enables the use of a previously proposed parallel-in-time solution for optimal control problems, which we adapt to the current problem. The structure of the resulting optimal control problem admits a parallel solution based on parallel associative scan algorithms. In the linear Gaussian special case, it yields a parallel Kalman-Bucy filter and a parallel continuous-time Rauch-Tung-Striebel smoother. These linear computational methods are further extended to nonlinear continuous-time state-space models through Taylor expansions. We also present the corresponding parallel two-filter smoother. The graphics processing unit (GPU) experiments on linear and nonlinear models demonstrate that the proposed framework achieves a significant speedup in computations while maintaining the accuracy of sequential algorithms.

Proximal Approximate Inference in State-Space Models

We present a class of algorithms for state estimation in nonlinear, non-Gaussian state-space models. Our approach is based on a variational Lagrangian formulation that casts Bayesian inference as a sequence of entropic trust-region updates subject to dynamic constraints. This framework gives rise to a family of forward-backward algorithms, whose structure is determined by the chosen factorization of the variational posterior. By focusing on Gauss--Markov approximations, we derive recursive schemes with favorable computational complexity. For general nonlinear, non-Gaussian models we close the recursions using generalized statistical linear regression and Fourier--Hermite moment matching.

Online Bayesian Experimental Design for Partially Observed Dynamical Systems

Bayesian experimental design (BED) provides a principled framework for optimizing data collection, but existing approaches do not apply to crucial real-world settings such as dynamical systems with partial observability, where only noisy and incomplete observations are available. These systems are naturally modeled as state-space models (SSMs), where latent states mediate the link between parameters and data, making the likelihood -- and thus information-theoretic objectives like the expected information gain (EIG) -- intractable. In addition, the dynamical nature of the system requires online algorithms that update posterior distributions and select designs sequentially in a computationally efficient manner. We address these challenges by deriving new estimators of the EIG and its gradient that explicitly marginalize latent states, enabling scalable stochastic optimization in nonlinear SSMs. Our approach leverages nested particle filters (NPFs) for efficient online inference with convergence guarantees. Applications to realistic models, such as the susceptible-infected-recovered (SIR) and a moving source location task, show that our framework successfully handles both partial observability and online computation.

Ultrafast Deep Learning-Based Scatter Estimation in Cone-Beam Computed Tomography

Purpose: Scatter artifacts drastically degrade the image quality of cone-beam computed tomography (CBCT) scans. Although deep learning-based methods show promise in estimating scatter from CBCT measurements, their deployment in mobile CBCT systems or edge devices is still limited due to the large memory footprint of the networks. This study addresses the issue by applying networks at varying resolutions and suggesting an optimal one, based on speed and accuracy. Methods: First, the reconstruction error in down-up sampling of CBCT scatter signal was examined at six resolutions by comparing four interpolation methods. Next, a recent state-of-the-art method was trained across five image resolutions and evaluated for the reductions in floating-point operations (FLOPs), inference times, and GPU memory requirements. Results: Reducing the input size and network parameters achieved a 78-fold reduction in FLOPs compared to the baseline method, while maintaining comarable performance in terms of mean-absolute-percentage-error (MAPE) and mean-square-error (MSE). Specifically, the MAPE decreased to 3.85% compared to 4.42%, and the MSE decreased to 1.34 \times 10^{-2} compared to 2.01 \times 10^{-2}. Inference time and GPU memory usage were reduced by factors of 16 and 12, respectively. Further experiments comparing scatter-corrected reconstructions on a large, simulated dataset and real CBCT scans from water and Sedentex CT phantoms clearly demonstrated the robustness of our method. Conclusion: This study highlights the underappreciated role of downsampling in deep learning-based scatter estimation. The substantial reduction in FLOPs and GPU memory requirements achieved by our method enables scatter correction in resource-constrained environments, such as mobile CBCT and edge devices.

Conditional Normalizing Flow Surrogate for Monte Carlo Prediction of Radiative Properties in Nanoparticle-Embedded Layers

We present a probabilistic, data-driven surrogate model for predicting the radiative properties of nanoparticle embedded scattering media. The model uses conditional normalizing flows, which learn the conditional distribution of optical outputs, including reflectance, absorbance, and transmittance, given input parameters such as the absorption coefficient, scattering coefficient, anisotropy factor, and particle size distribution. We generate training data using Monte Carlo radiative transfer simulations, with optical properties derived from Mie theory. Unlike conventional neural networks, the conditional normalizing flow model yields full posterior predictive distributions, enabling both accurate forecasts and principled uncertainty quantification. Our results demonstrate that this model achieves high predictive accuracy and reliable uncertainty estimates, establishing it as a powerful and efficient surrogate for radiative transfer simulations.

Sequential Monte Carlo for Policy Optimization in Continuous POMDPs

Optimal decision-making under partial observability requires agents to balance reducing uncertainty (exploration) against pursuing immediate objectives (exploitation). In this paper, we introduce a novel policy optimization framework for continuous partially observable Markov decision processes (POMDPs) that explicitly addresses this challenge. Our method casts policy learning as probabilistic inference in a non-Markovian Feynman--Kac model that inherently captures the value of information gathering by anticipating future observations, without requiring extrinsic exploration bonuses or handcrafted heuristics. To optimize policies under this model, we develop a nested sequential Monte Carlo~(SMC) algorithm that efficiently estimates a history-dependent policy gradient under samples from the optimal trajectory distribution induced by the POMDP. We demonstrate the effectiveness of our algorithm across standard continuous POMDP benchmarks, where existing methods struggle to act under uncertainty.

Statistical Linear Regression Approach to Kalman Filtering and Smoothing under Cyber-Attacks

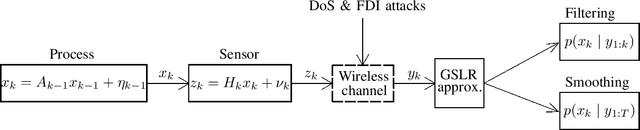
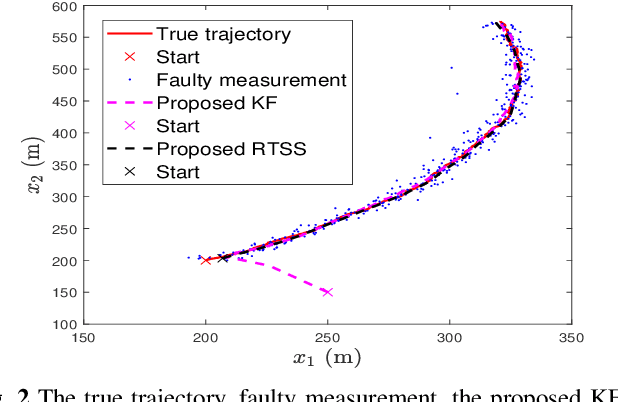
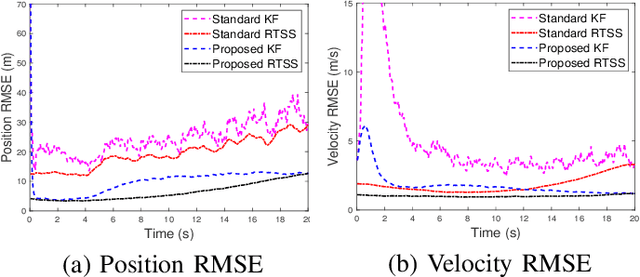
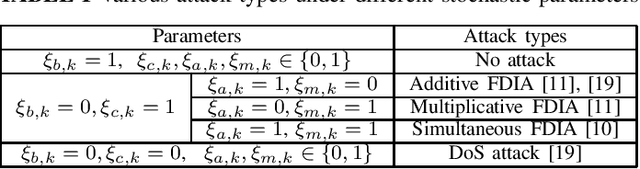
Remote state estimation in cyber-physical systems is often vulnerable to cyber-attacks due to wireless connections between sensors and computing units. In such scenarios, adversaries compromise the system by injecting false data or blocking measurement transmissions via denial-of-service attacks, distorting sensor readings. This paper develops a Kalman filter and Rauch--Tung--Striebel (RTS) smoother for linear stochastic state-space models subject to cyber-attacked measurements. We approximate the faulty measurement model via generalized statistical linear regression (GSLR). The GSLR-based approximated measurement model is then used to develop a Kalman filter and RTS smoother for the problem. The effectiveness of the proposed algorithms under cyber-attacks is demonstrated through a simulated aircraft tracking experiment.

Provable Quantum Algorithm Advantage for Gaussian Process Quadrature

The aim of this paper is to develop novel quantum algorithms for Gaussian process quadrature methods. Gaussian process quadratures are numerical integration methods where Gaussian processes are used as functional priors for the integrands to capture the uncertainty arising from the sparse function evaluations. Quantum computers have emerged as potential replacements for classical computers, offering exponential reductions in the computational complexity of machine learning tasks. In this paper, we combine Gaussian process quadratures and quantum computing by proposing a quantum low-rank Gaussian process quadrature method based on a Hilbert space approximation of the Gaussian process kernel and enhancing the quadrature using a quantum circuit. The method combines the quantum phase estimation algorithm with the quantum principal component analysis technique to extract information up to a desired rank. Then, Hadamard and SWAP tests are implemented to find the expected value and variance that determines the quadrature. We use numerical simulations of a quantum computer to demonstrate the effectiveness of the method. Furthermore, we provide a theoretical complexity analysis that shows a polynomial advantage over classical Gaussian process quadrature methods. The code is available at https://github.com/cagalvisf/Quantum_HSGPQ.

Gaussian multi-target filtering with target dynamics driven by a stochastic differential equation

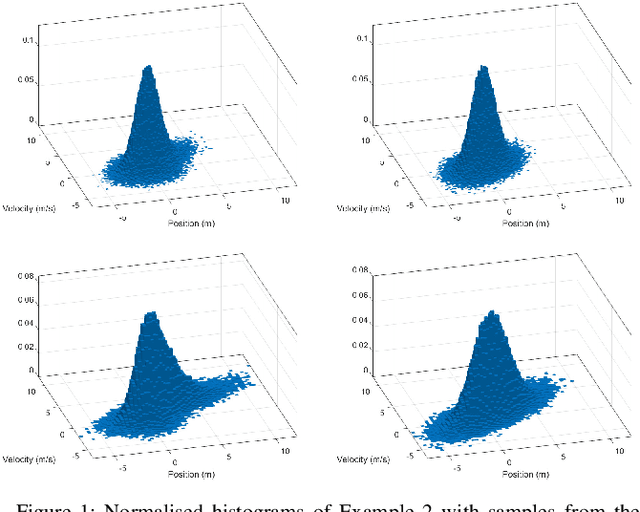
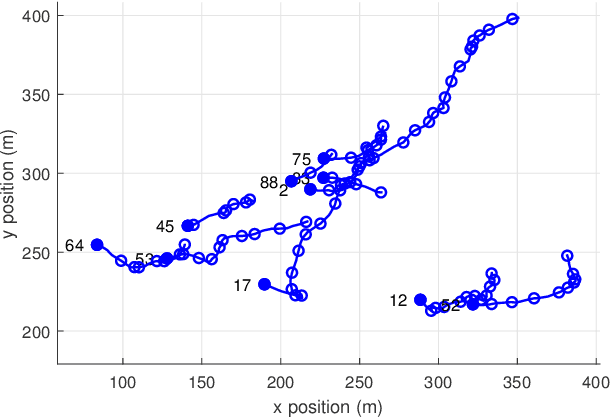
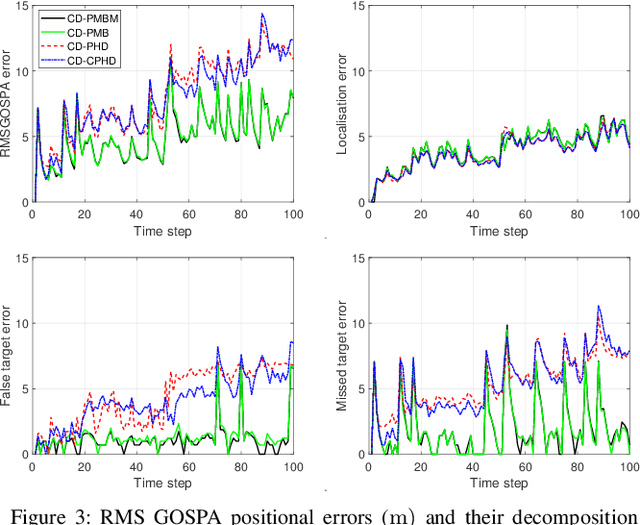
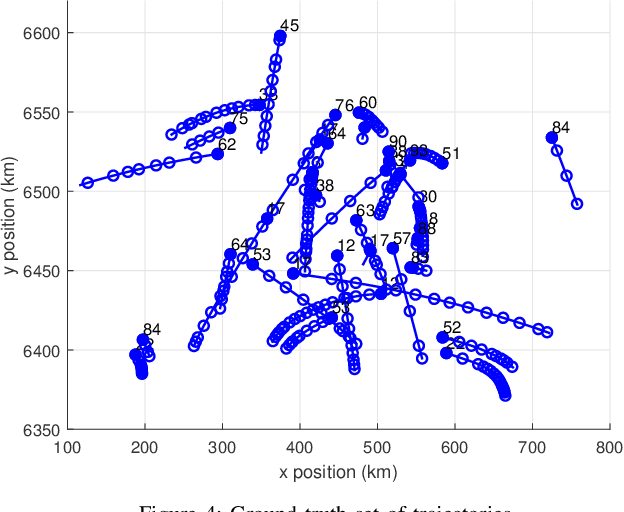
This paper proposes multi-target filtering algorithms in which target dynamics are given in continuous time and measurements are obtained at discrete time instants. In particular, targets appear according to a Poisson point process (PPP) in time with a given Gaussian spatial distribution, targets move according to a general time-invariant linear stochastic differential equation, and the life span of each target is modelled with an exponential distribution. For this multi-target dynamic model, we derive the distribution of the set of new born targets and calculate closed-form expressions for the best fitting mean and covariance of each target at its time of birth by minimising the Kullback-Leibler divergence via moment matching. This yields a novel Gaussian continuous-discrete Poisson multi-Bernoulli mixture (PMBM) filter, and its approximations based on Poisson multi-Bernoulli and probability hypothesis density filtering. These continuous-discrete multi-target filters are also extended to target dynamics driven by nonlinear stochastic differential equations.

A Parallel-in-Time Newton's Method for Nonlinear Model Predictive Control

Model predictive control (MPC) is a powerful framework for optimal control of dynamical systems. However, MPC solvers suffer from a high computational burden that restricts their application to systems with low sampling frequency. This issue is further amplified in nonlinear and constrained systems that require nesting MPC solvers within iterative procedures. In this paper, we address these issues by developing parallel-in-time algorithms for constrained nonlinear optimization problems that take advantage of massively parallel hardware to achieve logarithmic computational time scaling over the planning horizon. We develop time-parallel second-order solvers based on interior point methods and the alternating direction method of multipliers, leveraging fast convergence and lower computational cost per iteration. The parallelization is based on a reformulation of the subproblems in terms of associative operations that can be parallelized using the associative scan algorithm. We validate our approach on numerical examples of nonlinear and constrained dynamical systems.