Temporal parallelisation of continuous-time maximum-a-posteriori trajectory estimation

This paper proposes a parallel-in-time method for computing continuous-time maximum-a-posteriori (MAP) trajectory estimates of the states of partially observed stochastic differential equations (SDEs), with the goal of improving computational speed on parallel architectures. The MAP estimation problem is reformulated as a continuous-time optimal control problem based on the Onsager-Machlup functional. This reformulation enables the use of a previously proposed parallel-in-time solution for optimal control problems, which we adapt to the current problem. The structure of the resulting optimal control problem admits a parallel solution based on parallel associative scan algorithms. In the linear Gaussian special case, it yields a parallel Kalman-Bucy filter and a parallel continuous-time Rauch-Tung-Striebel smoother. These linear computational methods are further extended to nonlinear continuous-time state-space models through Taylor expansions. We also present the corresponding parallel two-filter smoother. The graphics processing unit (GPU) experiments on linear and nonlinear models demonstrate that the proposed framework achieves a significant speedup in computations while maintaining the accuracy of sequential algorithms.

Proximal Approximate Inference in State-Space Models

We present a class of algorithms for state estimation in nonlinear, non-Gaussian state-space models. Our approach is based on a variational Lagrangian formulation that casts Bayesian inference as a sequence of entropic trust-region updates subject to dynamic constraints. This framework gives rise to a family of forward-backward algorithms, whose structure is determined by the chosen factorization of the variational posterior. By focusing on Gauss--Markov approximations, we derive recursive schemes with favorable computational complexity. For general nonlinear, non-Gaussian models we close the recursions using generalized statistical linear regression and Fourier--Hermite moment matching.

Probabilistic Trajectory GOSPA: A Metric for Uncertainty-Aware Multi-Object Tracking Performance Evaluation

This paper presents a generalization of the trajectory general optimal sub-pattern assignment (GOSPA) metric for evaluating multi-object tracking algorithms that provide trajectory estimates with track-level uncertainties. This metric builds on the recently introduced probabilistic GOSPA metric to account for both the existence and state estimation uncertainties of individual object states. Similar to trajectory GOSPA (TGOSPA), it can be formulated as a multidimensional assignment problem, and its linear programming relaxation--also a valid metric--is computable in polynomial time. Additionally, this metric retains the interpretability of TGOSPA, and we show that its decomposition yields intuitive costs terms associated to expected localization error and existence probability mismatch error for properly detected objects, expected missed and false detection error, and track switch error. The effectiveness of the proposed metric is demonstrated through a simulation study.

Histogram-Probabilistic Multi-Hypothesis Tracking with Integrated Target Existence

The histogram-probabilistic multi-hypothesis tracker (H-PMHT) is a parametric approach to solving the multi-target track-before-detect (TBD) problem, using expectation maximisation (EM). A key limitation of this method is the assumption of a known and constant number of targets. In this paper, we propose the integrated existence Poisson histogram probabilistic multi-hypothesis tracker (IE-PHPMHT), for TBD of multiple targets. It extends the H-PMHT framework by adding a probability of existence to each potential target. For the derivation, we utilise a Poisson point process (PPP) measurement model and Bernoulli targets, allowing for a multi-Bernoulli birth process and an unknown, time-varying number of targets. Hence, integrated track management is achieved through the discrimination of track quality assessments based on existence probabilities. The algorithm is evaluated in a simulation study of two scenarios and is compared with several other algorithms, demonstrating its performance.

Poisson multi-Bernoulli mixture filter for trajectory measurements

This paper presents a Poisson multi-Bernoulli mixture (PMBM) filter for multi-target filtering based on sensor measurements that are sets of trajectories in the last two-time step window. The proposed filter, the trajectory measurement PMBM (TM-PMBM) filter, propagates a PMBM density on the set of target states. In prediction, the filter obtains the PMBM density on the set of trajectories over the last two time steps. This density is then updated with the set of trajectory measurements. After the update step, the PMBM posterior on the set of two-step trajectories is marginalised to obtain a PMBM density on the set of target states. The filter provides a closed-form solution for multi-target filtering based on sets of trajectory measurements, estimating the set of target states at the end of each time window. Additionally, the paper proposes computationally lighter alternatives to the TM-PMBM filter by deriving a Poisson multi-Bernoulli (PMB) density through Kullback-Leibler divergence minimisation in an augmented space with auxiliary variables. The performance of the proposed filters are evaluated in a simulation study.

MTS: A Deep Reinforcement Learning Portfolio Management Framework with Time-Awareness and Short-Selling

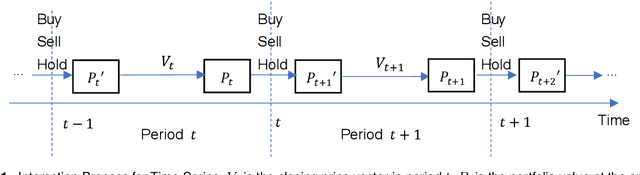
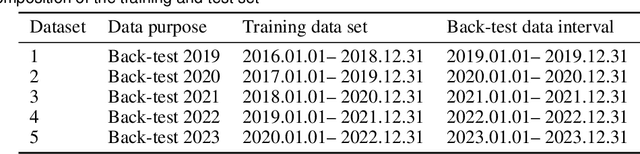
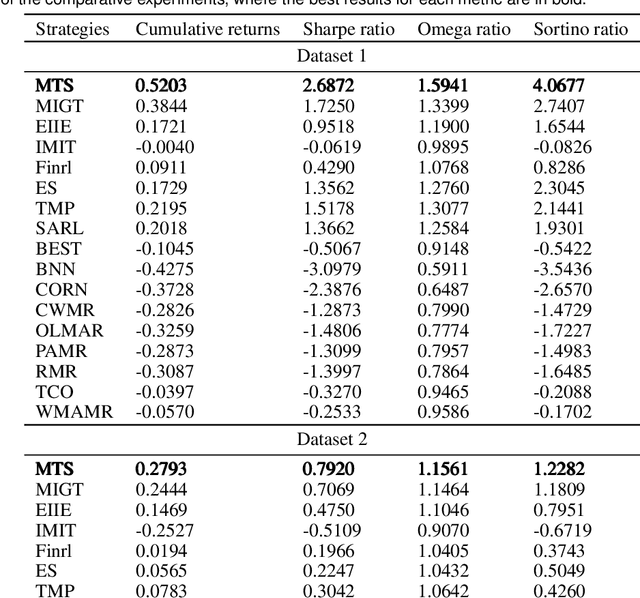
Portfolio management remains a crucial challenge in finance, with traditional methods often falling short in complex and volatile market environments. While deep reinforcement approaches have shown promise, they still face limitations in dynamic risk management, exploitation of temporal markets, and incorporation of complex trading strategies such as short-selling. These limitations can lead to suboptimal portfolio performance, increased vulnerability to market volatility, and missed opportunities in capturing potential returns from diverse market conditions. This paper introduces a Deep Reinforcement Learning Portfolio Management Framework with Time-Awareness and Short-Selling (MTS), offering a robust and adaptive strategy for sustainable investment performance. This framework utilizes a novel encoder-attention mechanism to address the limitations by incorporating temporal market characteristics, a parallel strategy for automated short-selling based on market trends, and risk management through innovative Incremental Conditional Value at Risk, enhancing adaptability and performance. Experimental validation on five diverse datasets from 2019 to 2023 demonstrates MTS's superiority over traditional algorithms and advanced machine learning techniques. MTS consistently achieves higher cumulative returns, Sharpe, Omega, and Sortino ratios, underscoring its effectiveness in balancing risk and return while adapting to market dynamics. MTS demonstrates an average relative increase of 30.67% in cumulative returns and 29.33% in Sharpe ratio compared to the next best-performing strategies across various datasets.

Probabilistic GOSPA: A Metric for Performance Evaluation of Multi-Object Filters with Uncertainties

This paper presents a probabilistic generalization of the generalized optimal subpattern assignment (GOSPA) metric, termed P-GOSPA metric. GOSPA is a popular metric for evaluating the distance between finite sets, typically in multi-object estimation applications. P-GOSPA extends GOSPA to the space of multi-Bernoulli set densities, incorporating the inherent uncertainty in probabilistic multi-object representations. In addition, P-GOSPA retains the interpretability of GOSPA, such as decomposability into localization, missed and false detection errors, in a sound manner. Examples and simulations are presented to demonstrate the efficacy of P-GOSPA.

TGOSPA Metric Parameters Selection and Evaluation for Visual Multi-object Tracking

Multi-object tracking algorithms are deployed in various applications, each with unique performance requirements. For example, track switches pose significant challenges for offline scene understanding, as they hinder the accuracy of data interpretation. Conversely, in online surveillance applications, their impact is often minimal. This disparity underscores the need for application-specific performance evaluations that are both simple and mathematically sound. The trajectory generalized optimal sub-pattern assignment (TGOSPA) metric offers a principled approach to evaluate multi-object tracking performance. It accounts for localization errors, the number of missed and false objects, and the number of track switches, providing a comprehensive assessment framework. This paper illustrates the effective use of the TGOSPA metric in computer vision tasks, addressing challenges posed by the need for application-specific scoring methodologies. By exploring the TGOSPA parameter selection, we enable users to compare, comprehend, and optimize the performance of algorithms tailored for specific tasks, such as target tracking and training of detector or re-ID modules.

Gaussian multi-target filtering with target dynamics driven by a stochastic differential equation

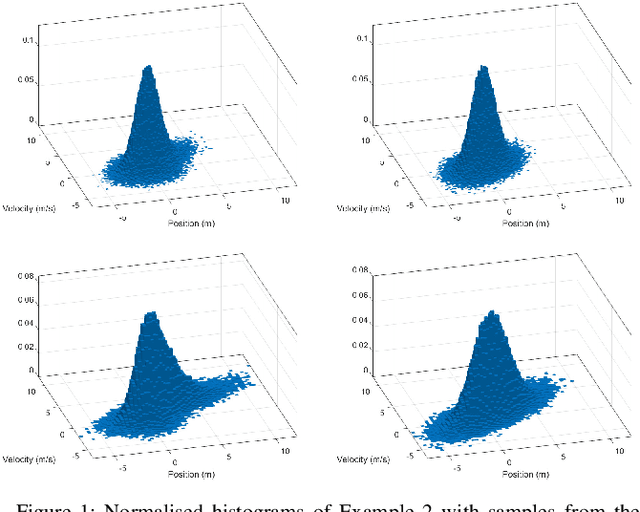
This paper proposes multi-target filtering algorithms in which target dynamics are given in continuous time and measurements are obtained at discrete time instants. In particular, targets appear according to a Poisson point process (PPP) in time with a given Gaussian spatial distribution, targets move according to a general time-invariant linear stochastic differential equation, and the life span of each target is modelled with an exponential distribution. For this multi-target dynamic model, we derive the distribution of the set of new born targets and calculate closed-form expressions for the best fitting mean and covariance of each target at its time of birth by minimising the Kullback-Leibler divergence via moment matching. This yields a novel Gaussian continuous-discrete Poisson multi-Bernoulli mixture (PMBM) filter, and its approximations based on Poisson multi-Bernoulli and probability hypothesis density filtering. These continuous-discrete multi-target filters are also extended to target dynamics driven by nonlinear stochastic differential equations.

Hybrid PHD-PMB Trajectory Smoothing Using Backward Simulation

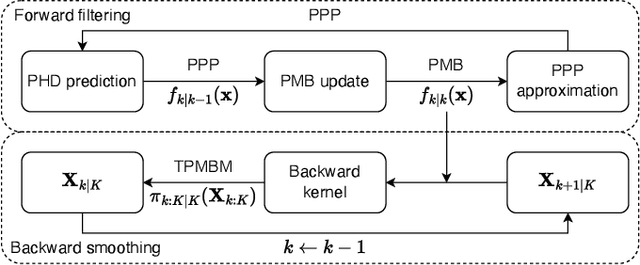
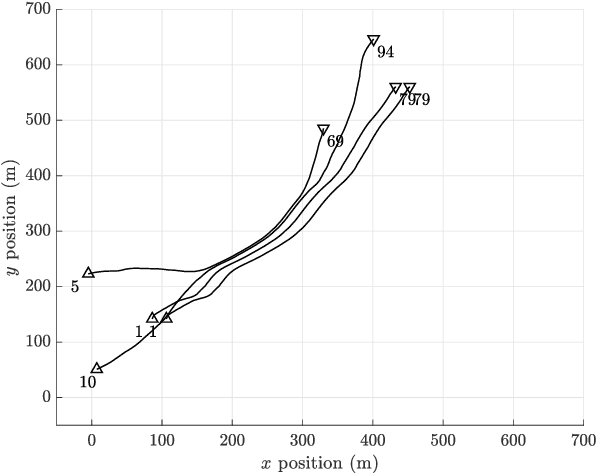
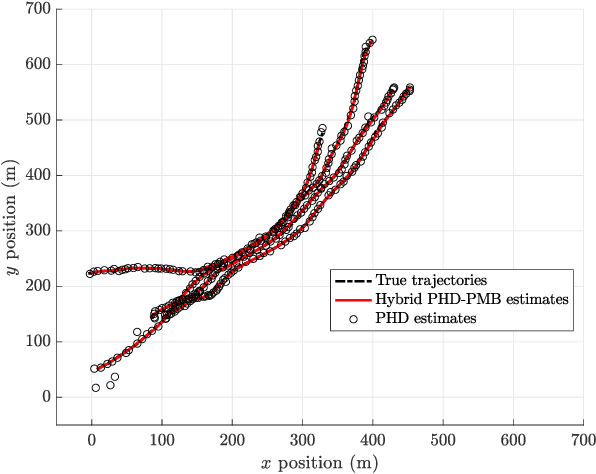
The probability hypothesis density (PHD) and Poisson multi-Bernoulli (PMB) filters are two popular set-type multi-object filters. Motivated by the fact that the multi-object filtering density after each update step in the PHD filter is a PMB without approximation, in this paper we present a multi-object smoother involving PHD forward filtering and PMB backward smoothing. This is achieved by first running the PHD filtering recursion in the forward pass and extracting the PMB filtering densities after each update step before the Poisson Point Process approximation, which is inherent in the PHD filter update. Then in the backward pass we apply backward simulation for sets of trajectories to the extracted PMB filtering densities. We call the resulting multi-object smoother hybrid PHD-PMB trajectory smoother. Notably, the hybrid PHD-PMB trajectory smoother can provide smoothed trajectory estimates for the PHD filter without labeling or tagging, which is not possible for existing PHD smoothers. Also, compared to the trajectory PHD filter, which can only estimate alive trajectories, the hybrid PHD-PMB trajectory smoother enables the estimation of the set of all trajectories. Simulation results demonstrate that the hybrid PHD-PMB trajectory smoother outperforms the PHD filter in terms of both state and cardinality estimates, and the trajectory PHD filter in terms of false detections.