A cutting plane algorithm for globally solving low dimensional k-means clustering problems

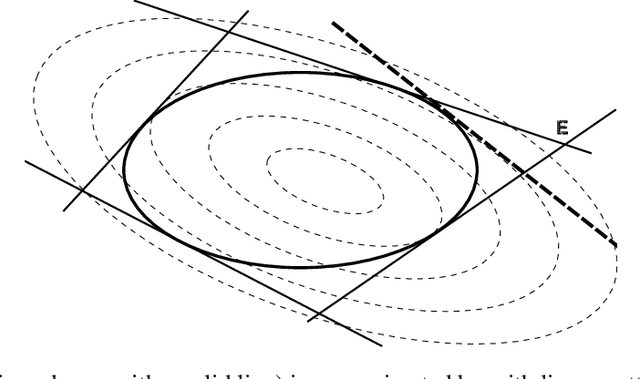
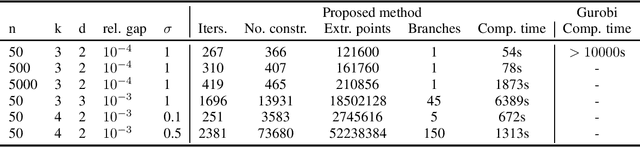
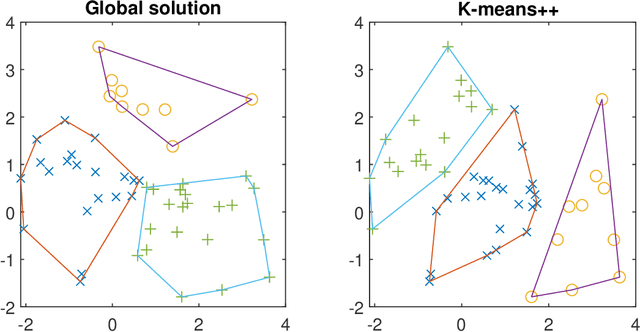
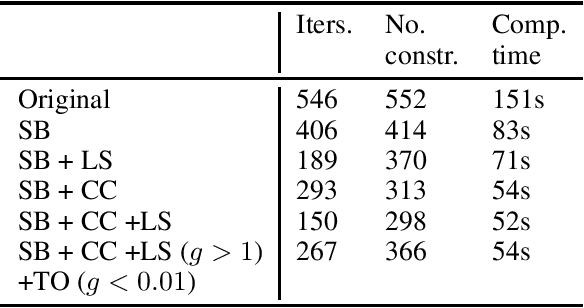
Clustering is one of the most fundamental tools in data science and machine learning, and k-means clustering is one of the most common such methods. There is a variety of approximate algorithms for the k-means problem, but computing the globally optimal solution is in general NP-hard. In this paper we consider the k-means problem for instances with low dimensional data and formulate it as a structured concave assignment problem. This allows us to exploit the low dimensional structure and solve the problem to global optimality within reasonable time for large data sets with several clusters. The method builds on iteratively solving a small concave problem and a large linear programming problem. This gives a sequence of feasible solutions along with bounds which we show converges to zero optimality gap. The paper combines methods from global optimization theory to accelerate the procedure, and we provide numerical results on their performance.

Globally solving the Gromov-Wasserstein problem for point clouds in low dimensional Euclidean spaces

This paper presents a framework for computing the Gromov-Wasserstein problem between two sets of points in low dimensional spaces, where the discrepancy is the squared Euclidean norm. The Gromov-Wasserstein problem is a generalization of the optimal transport problem that finds the assignment between two sets preserving pairwise distances as much as possible. This can be used to quantify the similarity between two formations or shapes, a common problem in AI and machine learning. The problem can be formulated as a Quadratic Assignment Problem (QAP), which is in general computationally intractable even for small problems. Our framework addresses this challenge by reformulating the QAP as an optimization problem with a low-dimensional domain, leveraging the fact that the problem can be expressed as a concave quadratic optimization problem with low rank. The method scales well with the number of points, and it can be used to find the global solution for large-scale problems with thousands of points. We compare the computational complexity of our approach with state-of-the-art methods on synthetic problems and apply it to a near-symmetrical problem which is of particular interest in computational biology.

Orthogonalization of data via Gromov-Wasserstein type feedback for clustering and visualization

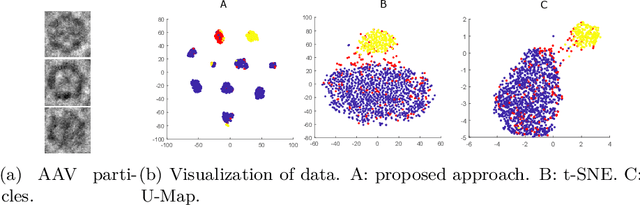
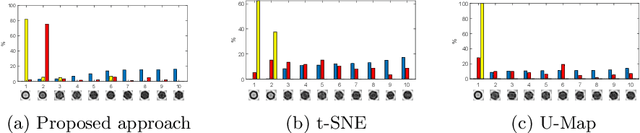
In this paper we propose an adaptive approach for clustering and visualization of data by an orthogonalization process. Starting with the data points being represented by a Markov process using the diffusion map framework, the method adaptively increase the orthogonality of the clusters by applying a feedback mechanism inspired by the Gromov-Wasserstein distance. This mechanism iteratively increases the spectral gap and refines the orthogonality of the data to achieve a clustering with high specificity. By using the diffusion map framework and representing the relation between data points using transition probabilities, the method is robust with respect to both the underlying distance, noise in the data and random initialization. We prove that the method converges globally to a unique fixpoint for certain parameter values. We also propose a related approach where the transition probabilities in the Markov process are required to be doubly stochastic, in which case the method generates a minimizer to a nonconvex optimization problem. We apply the method on cryo-electron microscopy image data from biopharmaceutical manufacturing where we can confirm biologically relevant insights related to therapeutic efficacy. We consider an example with morphological variations of gene packaging and confirm that the method produces biologically meaningful clustering results consistent with human expert classification.

Quantifying and Computing Covariance Uncertainty

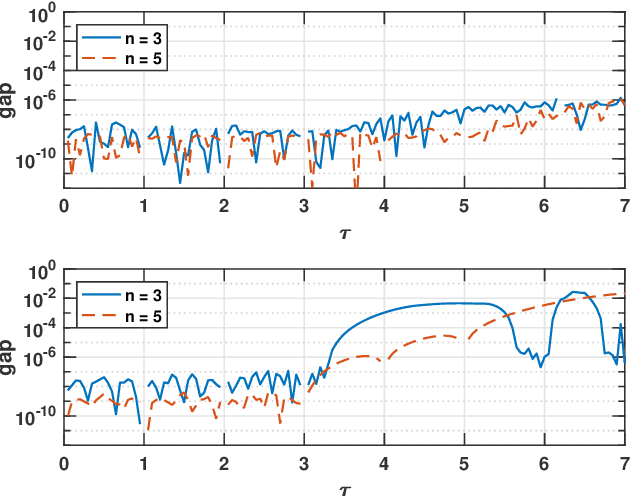
In this work, we consider the problem of bounding the values of a covariance function corresponding to a continuous-time stationary stochastic process or signal. Specifically, for two signals whose covariance functions agree on a finite discrete set of time-lags, we consider the maximal possible discrepancy of the covariance functions for real-valued time-lags outside this discrete grid. Computing this uncertainty corresponds to solving an infinite dimensional non-convex problem. However, we herein prove that the maximal objective value may be bounded from above by a finite dimensional convex optimization problem, allowing for efficient computation by standard methods. Furthermore, we empirically observe that for the case of signals whose spectra are supported on an interval, this upper bound is sharp, i.e., provides an exact quantification of the covariance uncertainty.

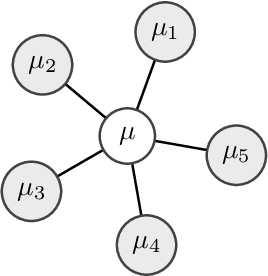
On the complexity of the optimal transport problem with graph-structured cost

Multi-marginal optimal transport (MOT) is a generalization of optimal transport to multiple marginals. Optimal transport has evolved into an important tool in many machine learning applications, and its multi-marginal extension opens up for addressing new challenges in the field of machine learning. However, the usage of MOT has been largely impeded by its computational complexity which scales exponentially in the number of marginals. Fortunately, in many applications, such as barycenter or interpolation problems, the cost function adheres to structures, which has recently been exploited for developing efficient computational methods. In this work we derive computational bounds for these methods. With $m$ marginal distributions supported on $n$ points, we provide a $ \mathcal{\tilde O}(d(G)m n^2\epsilon^{-2})$ bound for a $\epsilon$-accuracy when the problem is associated with a tree with diameter $d(G)$. For the special case of the Wasserstein barycenter problem, which corresponds to a star-shaped tree, our bound is in alignment with the existing complexity bound for it.

Mixed-Spectrum Signals -- Discrete Approximations and Variance Expressions for Covariance Estimates

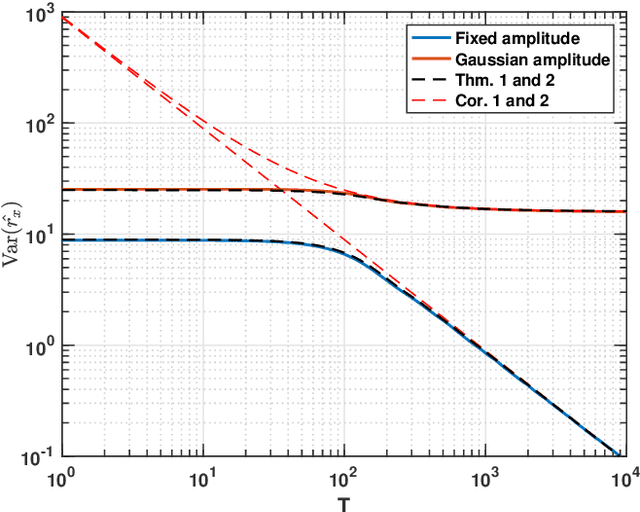
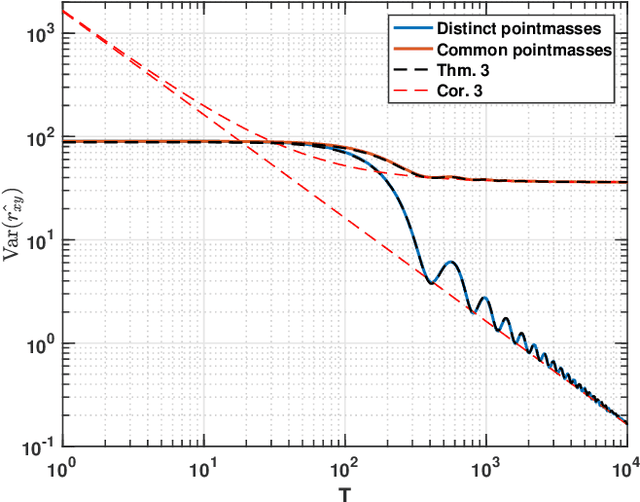
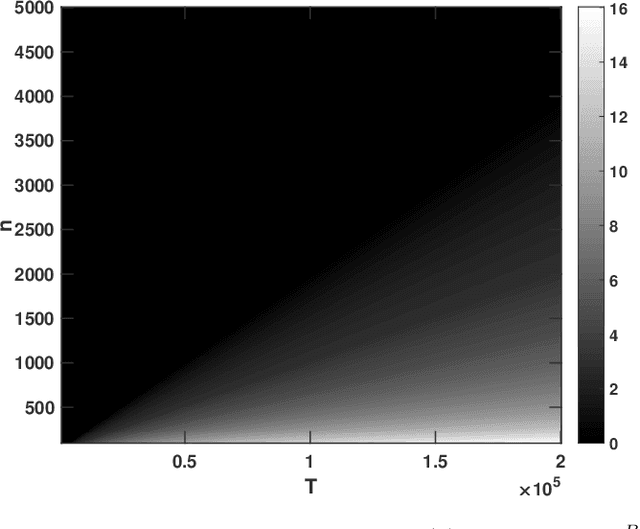
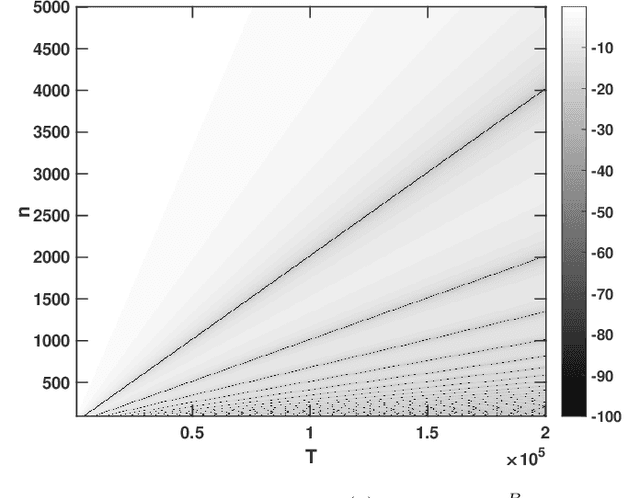
The estimation of the covariance function of a stochastic process, or signal, is of integral importance for a multitude of signal processing applications. In this work, we derive closed-form expressions for the variance of covariance estimates for mixed-spectrum signals, i.e., spectra containing both absolutely continuous and singular parts. The results cover both finite-sample and asymptotic regimes, allowing for assessing the exact speed of convergence of estimates to their expectations, as well as their limiting behavior. As is shown, such covariance estimates may converge even for non-ergodic processes. Furthermore, we consider approximating signals with arbitrary spectral densities by sequences of singular spectrum, i.e., sinusoidal, processes, and derive the limiting behavior of covariance estimates as both the sample size and the number of sinusoidal components tend to infinity. We show that the asymptotic regime variance can be described by a time-frequency resolution product, with dramatically different behavior depending on how the sinusoidal approximation is constructed. In a few numerical examples we illustrate the theory and the corresponding implications for direction of arrival estimation.

Is this Harmful? Learning to Predict Harmfulness Ratings from Video

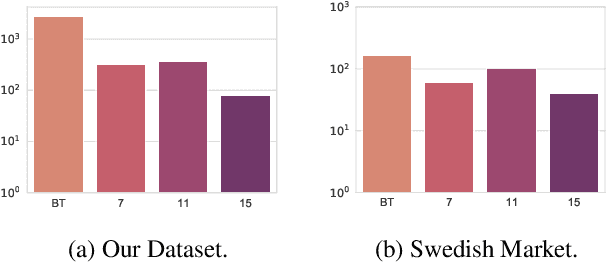
Automatically identifying harmful content in video is an important task with a wide range of applications. However, due to the difficulty of collecting high-quality labels as well as demanding computational requirements, the task has not had a satisfying general approach. Typically, only small subsets of the problem are considered, such as identifying violent content. In cases where the general problem is tackled, rough approximations and simplifications are made to deal with the lack of labels and computational complexity. In this work, we identify and tackle the two main obstacles. First, we create a dataset of approximately 4000 video clips, annotated by professionals in the field. Secondly, we demonstrate that advances in video recognition enable training models on our dataset that consider the full context of the scene. We conduct an in-depth study on our modeling choices and find that we greatly benefit from combining the visual and audio modality and that pretraining on large-scale video recognition datasets and class balanced sampling further improves performance. We additionally perform a qualitative study that reveals the heavily multi-modal nature of our dataset. Our dataset will be made available upon publication.

Incremental inference of collective graphical models

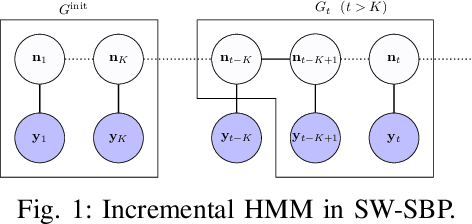
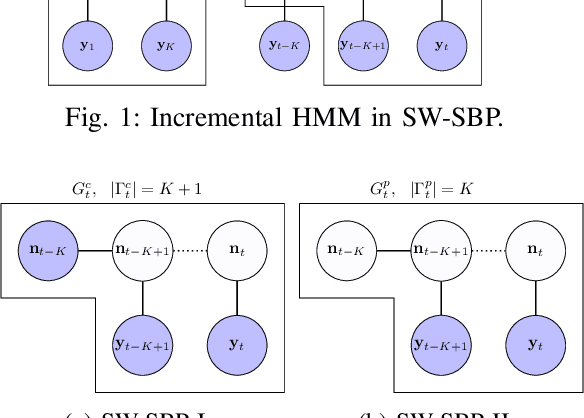
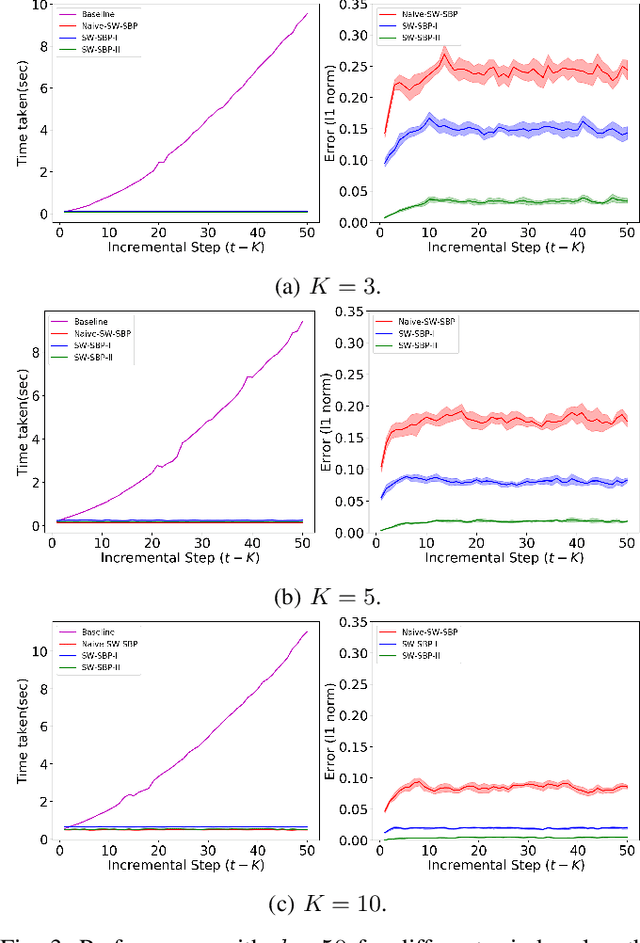
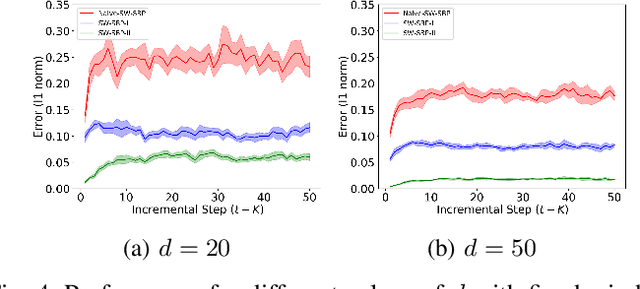
We consider incremental inference problems from aggregate data for collective dynamics. In particular, we address the problem of estimating the aggregate marginals of a Markov chain from noisy aggregate observations in an incremental (online) fashion. We propose a sliding window Sinkhorn belief propagation (SW-SBP) algorithm that utilizes a sliding window filter of the most recent noisy aggregate observations along with encoded information from discarded observations. Our algorithm is built upon the recently proposed multi-marginal optimal transport based SBP algorithm that leverages standard belief propagation and Sinkhorn algorithm to solve inference problems from aggregate data. We demonstrate the performance of our algorithm on applications such as inferring population flow from aggregate observations.

Multi-marginal optimal transport and probabilistic graphical models

We study multi-marginal optimal transport problems from a probabilistic graphical model perspective. We point out an elegant connection between the two when the underlying cost for optimal transport allows a graph structure. In particular, an entropy regularized multi-marginal optimal transport is equivalent to a Bayesian marginal inference problem for probabilistic graphical models with the additional requirement that some of the marginal distributions are specified. This relation on the one hand extends the optimal transport as well as the probabilistic graphical model theories, and on the other hand leads to fast algorithms for multi-marginal optimal transport by leveraging the well-developed algorithms in Bayesian inference. Several numerical examples are provided to highlight the results.

Inference with Aggregate Data: An Optimal Transport Approach

We consider inference problems over probabilistic graphical models with aggregate data. In particular, we propose a new efficient belief propagation type algorithm over tree-structured graphs with polynomial computational complexity as well as a global convergence guarantee. This is in contrast to previous methods that either exhibit prohibitive complexity as the population grows or do not guarantee convergence. Our method is based on optimal transport, or more specifically, multi-marginal optimal transport theory. In particular, the inference problem with aggregate observations we consider in this paper can be seen as a structured multi-marginal optimal transport problem, where the cost function decomposes according to the underlying graph. Consequently, the celebrated Sinkhorn algorithm for multi-marginal optimal transport can be leveraged, together with the standard belief propagation algorithm to establish an efficient inference scheme. We demonstrate the performance of our algorithm on applications such as inferring population flow from aggregate observations.