Mixed-Spectrum Signals -- Discrete Approximations and Variance Expressions for Covariance Estimates
Paper and Code
Jun 28, 2021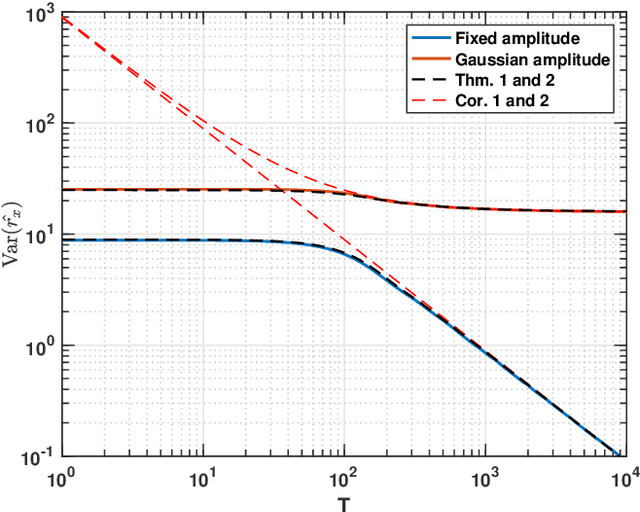
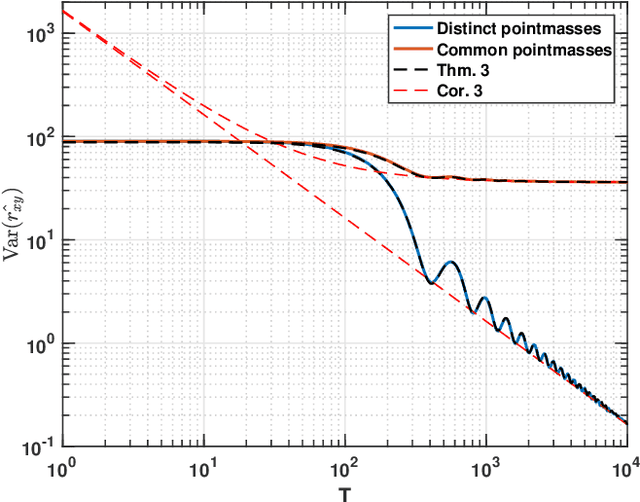
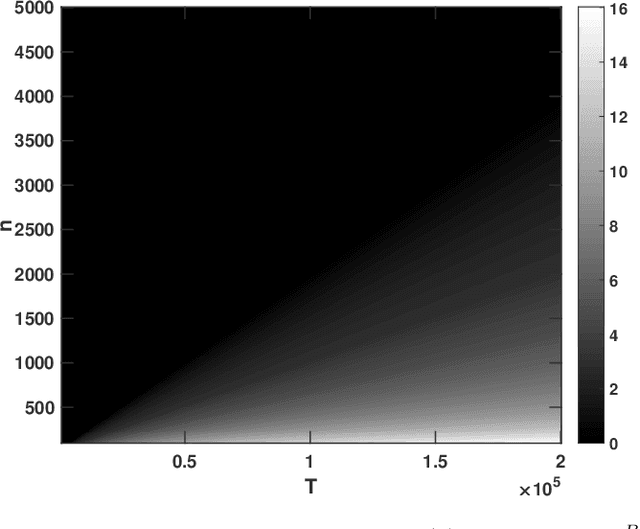
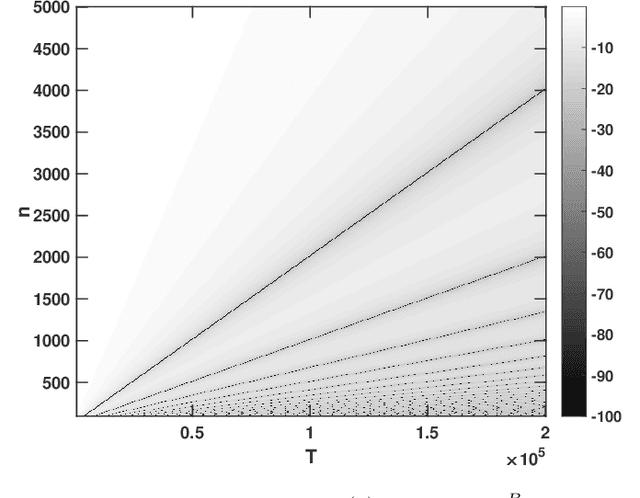
The estimation of the covariance function of a stochastic process, or signal, is of integral importance for a multitude of signal processing applications. In this work, we derive closed-form expressions for the variance of covariance estimates for mixed-spectrum signals, i.e., spectra containing both absolutely continuous and singular parts. The results cover both finite-sample and asymptotic regimes, allowing for assessing the exact speed of convergence of estimates to their expectations, as well as their limiting behavior. As is shown, such covariance estimates may converge even for non-ergodic processes. Furthermore, we consider approximating signals with arbitrary spectral densities by sequences of singular spectrum, i.e., sinusoidal, processes, and derive the limiting behavior of covariance estimates as both the sample size and the number of sinusoidal components tend to infinity. We show that the asymptotic regime variance can be described by a time-frequency resolution product, with dramatically different behavior depending on how the sinusoidal approximation is constructed. In a few numerical examples we illustrate the theory and the corresponding implications for direction of arrival estimation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge