All-pole centroids in the Wasserstein metric with applications to clustering of spectral densities

In this work, we propose a method for computing centroids, or barycenters, in the spectral Wasserstein-2 metric for sets of power spectral densities, where the barycenters are restricted to belong to the set of all-pole spectra with a certain model order. This may be interpreted as finding an autoregressive representative for sets of second-order stationary Gaussian processes. While Wasserstein, or optimal transport, barycenters have been successfully used earlier in problems of spectral estimation and clustering, the resulting barycenters are non-parametric and the complexity of representing and storing them depends on, e.g., the choice of discretization grid. In contrast, the herein proposed method yields compact, low-dimensional, and interpretable spectral centroids that can be used in downstream tasks. Computing the all-pole centroids corresponds to solving a non-convex optimization problem in the model parameters, and we present a gradient descent scheme for addressing this. Although convergence to a globally optimal point cannot be guaranteed, the sub-optimality of the obtained centroids can be quantified. The proposed method is illustrated on a problem of phoneme classification.

Sound Field Estimation Using Optimal Transport Barycenters in the Presence of Phase Errors

This study introduces a novel approach for estimating plane-wave coefficients in sound field reconstruction, specifically addressing challenges posed by error-in-variable phase perturbations. Such systematic errors typically arise from sensor mis-calibration, including uncertainties in sensor positions and response characteristics, leading to measurement-induced phase shifts in plane wave coefficients. Traditional methods often result in biased estimates or non-convex solutions. To overcome these issues, we propose an optimal transport (OT) framework. This framework operates on a set of lifted non-negative measures that correspond to observation-dependent shifted coefficients relative to the unperturbed ones. By applying OT, the supports of the measures are transported toward an optimal average in the phase space, effectively morphing them into an indistinguishable state. This optimal average, known as barycenter, is linked to the estimated plane-wave coefficients using the same lifting rule. The framework addresses the ill-posed nature of the problem, due to the large number of plane waves, by adding a constant to the ground cost, ensuring the sparsity of the transport matrix. Convex consistency of the solution is maintained. Simulation results confirm that our proposed method provides more accurate coefficient estimations compared to baseline approaches in scenarios with both additive noise and phase perturbations.

Boundary-Informed Sound Field Reconstruction

We consider the problem of reconstructing the sound field in a room using prior information of the boundary geometry, represented as a point cloud. In general, when no boundary information is available, an accurate sound field reconstruction over a large spatial region and at high frequencies requires numerous microphone measurements. On the other hand, if all geometrical and acoustical aspects of the boundaries are known, the sound field could, in theory, be simulated without any measurements. In this work, we address the intermediate case, where only partial or uncertain boundary information is available. This setting is similar to one studied in virtual reality applications, where the goal is to create a perceptually convincing audio experience. In this work, we focus on spatial sound control applications, which in contrast require an accurate sound field reconstruction. Therefore, we formulate the problem within a linear Bayesian framework, incorporating a boundary-informed prior derived from impedance boundary conditions. The formulation allows for joint optimization of the unknown hyperparameters, including the noise and signal variances and the impedance boundary conditions. Using numerical experiments, we show that incorporating the boundary-informed prior significantly enhances the reconstruction, notably even when only a few hundreds of boundary points are available or when the boundary positions are calibrated with an uncertainty up to 1 dm.

Joint Spectrogram Separation and TDOA Estimation using Optimal Transport

Separating sources is a common challenge in applications such as speech enhancement and telecommunications, where distinguishing between overlapping sounds helps reduce interference and improve signal quality. Additionally, in multichannel systems, correct calibration and synchronization are essential to separate and locate source signals accurately. This work introduces a method for blind source separation and estimation of the Time Difference of Arrival (TDOA) of signals in the time-frequency domain. Our proposed method effectively separates signal mixtures into their original source spectrograms while simultaneously estimating the relative delays between receivers, using Optimal Transport (OT) theory. By exploiting the structure of the OT problem, we combine the separation and delay estimation processes into a unified framework, optimizing the system through a block coordinate descent algorithm. We analyze the performance of the OT-based estimator under various noise conditions and compare it with conventional TDOA and source separation methods. Numerical simulation results demonstrate that our proposed approach can achieve a significant level of accuracy across diverse noise scenarios for physical speech signals in both TDOA and source separation tasks.

Room Impulse Response Estimation through Optimal Mass Transport Barycenters

In this work, we consider the problem of jointly estimating a set of room impulse responses (RIRs) corresponding to closely spaced microphones. The accurate estimation of RIRs is crucial in acoustic applications such as speech enhancement, noise cancellation, and auralization. However, real-world constraints such as short excitation signals, low signal-to-noise ratios, and poor spectral excitation, often render the estimation problem ill-posed. In this paper, we address these challenges by means of optimal mass transport (OMT) regularization. In particular, we propose to use an OMT barycenter, or generalized mean, as a mechanism for information sharing between the microphones. This allows us to quantify and exploit similarities in the delay-structures between the different microphones without having to impose rigid assumptions on the room acoustics. The resulting estimator is formulated in terms of the solution to a convex optimization problem which can be implemented using standard solvers. In numerical examples, we demonstrate the potential of the proposed method in addressing otherwise ill-conditioned estimation scenarios.

A Diffusion-Based Generative Equalizer for Music Restoration

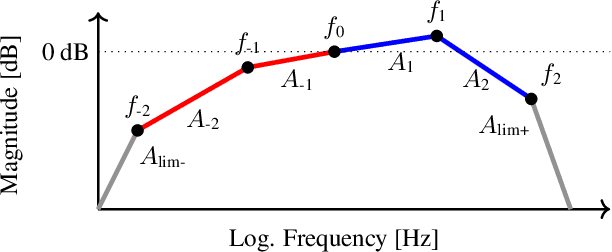
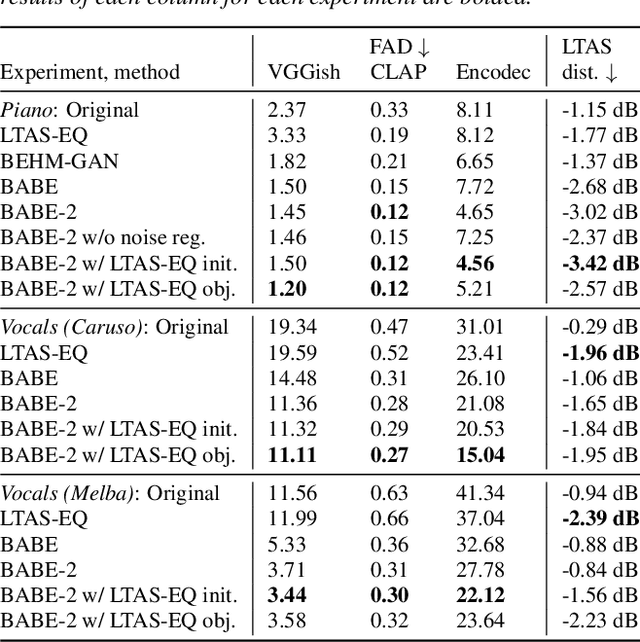
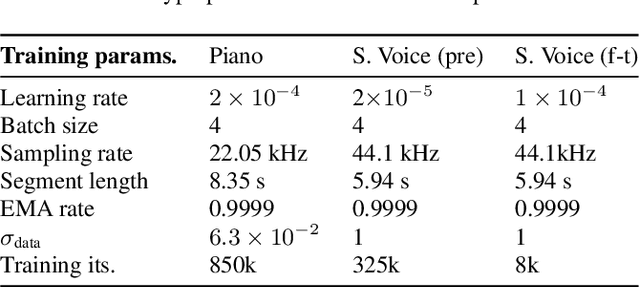
This paper presents a novel approach to audio restoration, focusing on the enhancement of low-quality music recordings, and in particular historical ones. Building upon a previous algorithm called BABE, or Blind Audio Bandwidth Extension, we introduce BABE-2, which presents a series of significant improvements. This research broadens the concept of bandwidth extension to \emph{generative equalization}, a novel task that, to the best of our knowledge, has not been explicitly addressed in previous studies. BABE-2 is built around an optimization algorithm utilizing priors from diffusion models, which are trained or fine-tuned using a curated set of high-quality music tracks. The algorithm simultaneously performs two critical tasks: estimation of the filter degradation magnitude response and hallucination of the restored audio. The proposed method is objectively evaluated on historical piano recordings, showing a marked enhancement over the prior version. The method yields similarly impressive results in rejuvenating the works of renowned vocalists Enrico Caruso and Nellie Melba. This research represents an advancement in the practical restoration of historical music.

Multi-Source Localization and Data Association for Time-Difference of Arrival Measurements

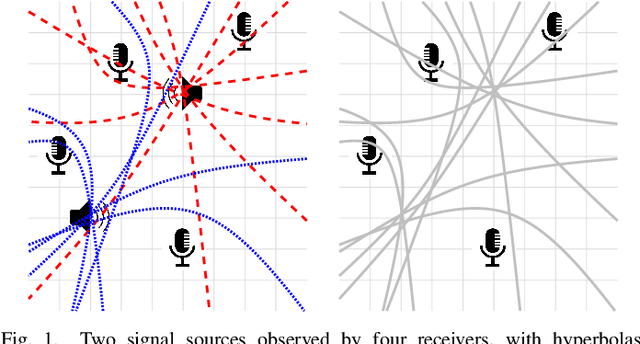
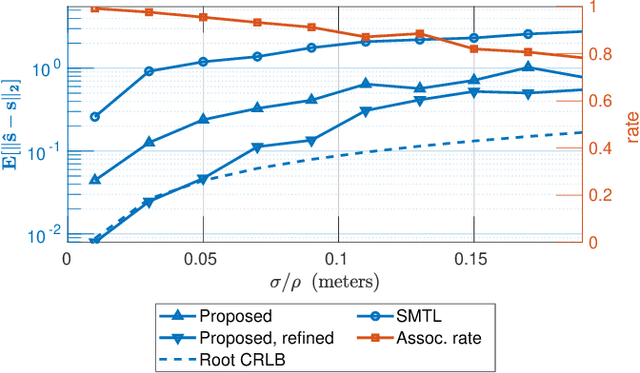
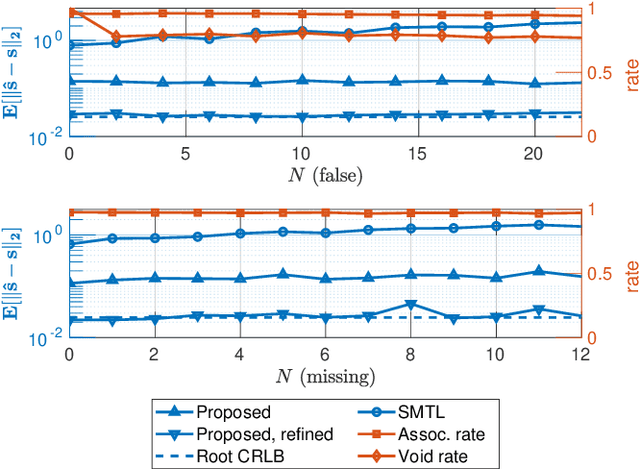
In this work, we consider the problem of localizing multiple signal sources based on time-difference of arrival (TDOA) measurements. In the blind setting, in which the source signals are not known, the localization task is challenging due to the data association problem. That is, it is not known which of the TDOA measurements correspond to the same source. Herein, we propose to perform joint localization and data association by means of an optimal transport formulation. The method operates by finding optimal groupings of TDOA measurements and associating these with candidate source locations. To allow for computationally feasible localization in three-dimensional space, an efficient set of candidate locations is constructed using a minimal multilateration solver based on minimal sets of receiver pairs. In numerical simulations, we demonstrate that the proposed method is robust both to measurement noise and TDOA detection errors. Furthermore, it is shown that the data association provided by the proposed method allows for statistically efficient estimates of the source locations.

Room Impulse Response Estimation using Optimal Transport: Simulation-Informed Inference

The ability to accurately estimate room impulse responses (RIRs) is integral to many applications of spatial audio processing. Regrettably, estimating the RIR using ambient signals, such as speech or music, remains a challenging problem due to, e.g., low signal-to-noise ratios, finite sample lengths, and poor spectral excitation. Commonly, in order to improve the conditioning of the estimation problem, priors are placed on the amplitudes of the RIR. Although serving as a regularizer, this type of prior is generally not useful when only approximate knowledge of the delay structure is available, which, for example, is the case when the prior is a simulated RIR from an approximation of the room geometry. In this work, we target the delay structure itself, constructing a prior based on the concept of optimal transport. As illustrated using both simulated and measured data, the resulting method is able to beneficially incorporate information even from simple simulation models, displaying considerable robustness to perturbations in the assumed room dimensions and its temperature.

Multi-frequency tracking via group-sparse optimal transport

In this work, we introduce an optimal transport framework for inferring power distributions over both spatial location and temporal frequency. Recently, it has been shown that optimal transport is a powerful tool for estimating spatial spectra that change smoothly over time. In this work, we consider the tracking of the spatio-temporal spectrum corresponding to a small number of moving broad-band signal sources. Typically, such tracking problems are addressed by treating the spatio-temporal power distribution in a frequency-by-frequency manner, allowing to use well-understood models for narrow-band signals. This however leads to decreased target resolution due to inefficient use of the available information. We propose an extension of the optimal transport framework that exploits information from several frequencies simultaneously by estimating a spatio-temporal distribution penalized by a group-sparsity regularizer. This approach finds a spatial spectrum that changes smoothly over time, and at each time instance has a small support that is similar across frequencies. To the best of the authors knowledge, this is the first formulation combining optimal transport and sparsity for solving inverse problems. As is shown on simulated and real data, our method can successfully track targets in scenarios where information from separate frequency bands alone is insufficient.

Zero-Shot Blind Audio Bandwidth Extension

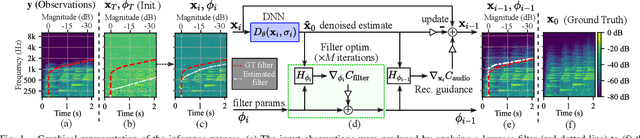
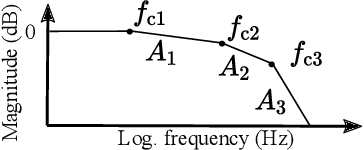
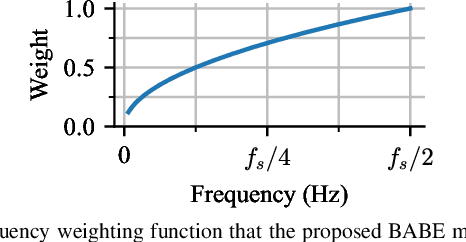
Audio bandwidth extension involves the realistic reconstruction of high-frequency spectra from bandlimited observations. In cases where the lowpass degradation is unknown, such as in restoring historical audio recordings, this becomes a blind problem. This paper introduces a novel method called BABE (Blind Audio Bandwidth Extension) that addresses the blind problem in a zero-shot setting, leveraging the generative priors of a pre-trained unconditional diffusion model. During the inference process, BABE utilizes a generalized version of diffusion posterior sampling, where the degradation operator is unknown but parametrized and inferred iteratively. The performance of the proposed method is evaluated using objective and subjective metrics, and the results show that BABE surpasses state-of-the-art blind bandwidth extension baselines and achieves competitive performance compared to non-blind filter-informed methods when tested with synthetic data. Moreover, BABE exhibits robust generalization capabilities when enhancing real historical recordings, effectively reconstructing the missing high-frequency content while maintaining coherence with the original recording. Subjective preference tests confirm that BABE significantly improves the audio quality of historical music recordings. Examples of historical recordings restored with the proposed method are available on the companion webpage: (http://research.spa.aalto.fi/publications/papers/ieee-taslp-babe/)