Joint Spectrogram Separation and TDOA Estimation using Optimal Transport

Separating sources is a common challenge in applications such as speech enhancement and telecommunications, where distinguishing between overlapping sounds helps reduce interference and improve signal quality. Additionally, in multichannel systems, correct calibration and synchronization are essential to separate and locate source signals accurately. This work introduces a method for blind source separation and estimation of the Time Difference of Arrival (TDOA) of signals in the time-frequency domain. Our proposed method effectively separates signal mixtures into their original source spectrograms while simultaneously estimating the relative delays between receivers, using Optimal Transport (OT) theory. By exploiting the structure of the OT problem, we combine the separation and delay estimation processes into a unified framework, optimizing the system through a block coordinate descent algorithm. We analyze the performance of the OT-based estimator under various noise conditions and compare it with conventional TDOA and source separation methods. Numerical simulation results demonstrate that our proposed approach can achieve a significant level of accuracy across diverse noise scenarios for physical speech signals in both TDOA and source separation tasks.

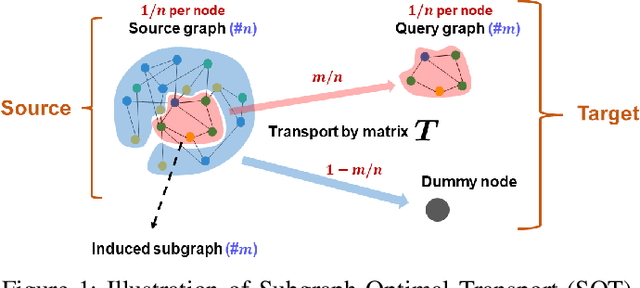
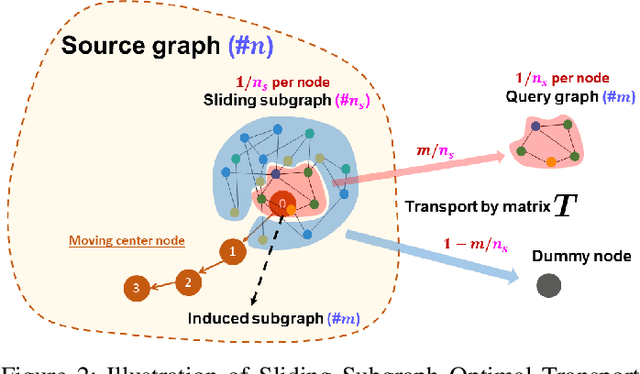
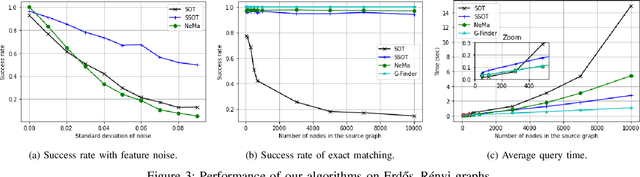
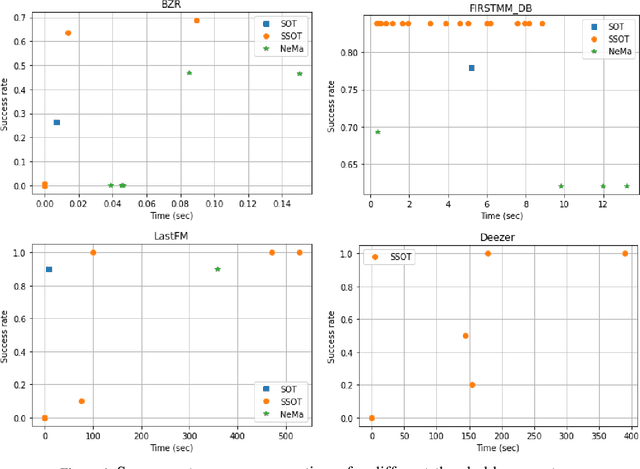
Subgraph Matching via Partial Optimal Transport

In this work, we propose a novel approach for subgraph matching, the problem of finding a given query graph in a large source graph, based on the fused Gromov-Wasserstein distance. We formulate the subgraph matching problem as a partial fused Gromov-Wasserstein problem, which allows us to build on existing theory and computational methods in order to solve this challenging problem. We extend our method by employing a subgraph sliding approach, which makes it efficient even for large graphs. In numerical experiments, we showcase that our new algorithms have the ability to outperform state-of-the-art methods for subgraph matching on synthetic as well as realworld datasets. In particular, our methods exhibit robustness with respect to noise in the datasets and achieve very fast query times.

Multi-frequency tracking via group-sparse optimal transport

In this work, we introduce an optimal transport framework for inferring power distributions over both spatial location and temporal frequency. Recently, it has been shown that optimal transport is a powerful tool for estimating spatial spectra that change smoothly over time. In this work, we consider the tracking of the spatio-temporal spectrum corresponding to a small number of moving broad-band signal sources. Typically, such tracking problems are addressed by treating the spatio-temporal power distribution in a frequency-by-frequency manner, allowing to use well-understood models for narrow-band signals. This however leads to decreased target resolution due to inefficient use of the available information. We propose an extension of the optimal transport framework that exploits information from several frequencies simultaneously by estimating a spatio-temporal distribution penalized by a group-sparsity regularizer. This approach finds a spatial spectrum that changes smoothly over time, and at each time instance has a small support that is similar across frequencies. To the best of the authors knowledge, this is the first formulation combining optimal transport and sparsity for solving inverse problems. As is shown on simulated and real data, our method can successfully track targets in scenarios where information from separate frequency bands alone is insufficient.

Bures-Wasserstein Means of Graphs

Finding the mean of sampled data is a fundamental task in machine learning and statistics. However, in cases where the data samples are graph objects, defining a mean is an inherently difficult task. We propose a novel framework for defining a graph mean via embeddings in the space of smooth graph signal distributions, where graph similarity can be measured using the Wasserstein metric. By finding a mean in this embedding space, we can recover a mean graph that preserves structural information. We establish the existence and uniqueness of the novel graph mean, and provide an iterative algorithm for computing it. To highlight the potential of our framework as a valuable tool for practical applications in machine learning, it is evaluated on various tasks, including k-means clustering of structured graphs, classification of functional brain networks, and semi-supervised node classification in multi-layer graphs. Our experimental results demonstrate that our approach achieves consistent performance, outperforms existing baseline approaches, and improves state-of-the-art methods.

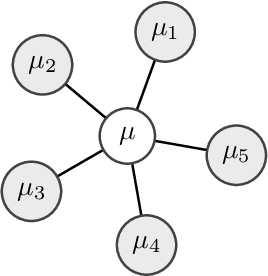
On the complexity of the optimal transport problem with graph-structured cost

Multi-marginal optimal transport (MOT) is a generalization of optimal transport to multiple marginals. Optimal transport has evolved into an important tool in many machine learning applications, and its multi-marginal extension opens up for addressing new challenges in the field of machine learning. However, the usage of MOT has been largely impeded by its computational complexity which scales exponentially in the number of marginals. Fortunately, in many applications, such as barycenter or interpolation problems, the cost function adheres to structures, which has recently been exploited for developing efficient computational methods. In this work we derive computational bounds for these methods. With $m$ marginal distributions supported on $n$ points, we provide a $ \mathcal{\tilde O}(d(G)m n^2\epsilon^{-2})$ bound for a $\epsilon$-accuracy when the problem is associated with a tree with diameter $d(G)$. For the special case of the Wasserstein barycenter problem, which corresponds to a star-shaped tree, our bound is in alignment with the existing complexity bound for it.

Incremental inference of collective graphical models

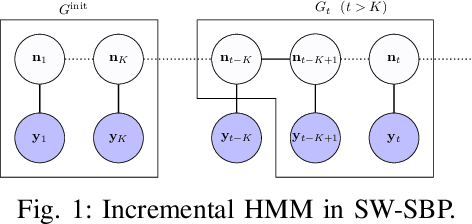
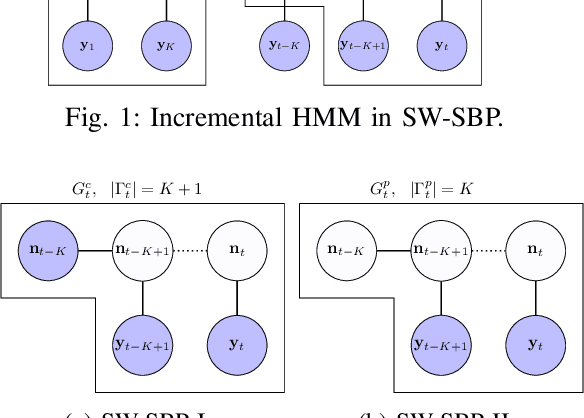
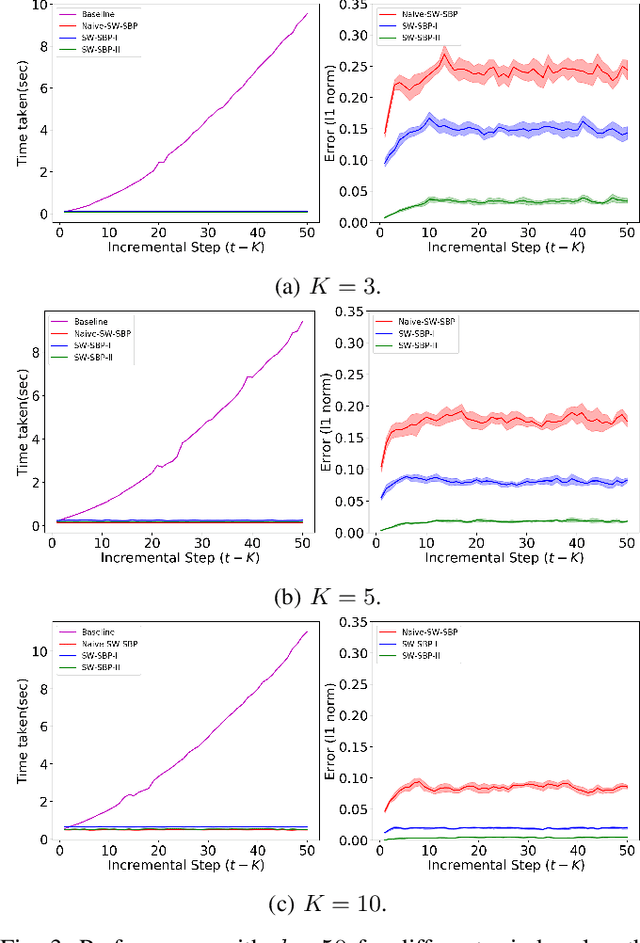
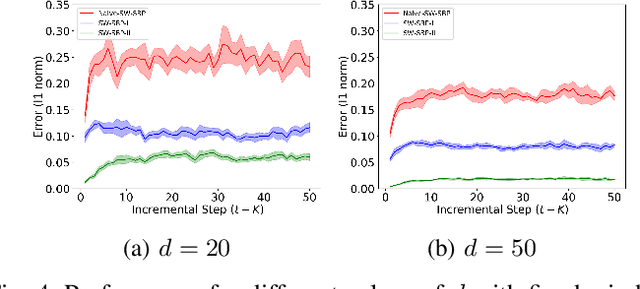
We consider incremental inference problems from aggregate data for collective dynamics. In particular, we address the problem of estimating the aggregate marginals of a Markov chain from noisy aggregate observations in an incremental (online) fashion. We propose a sliding window Sinkhorn belief propagation (SW-SBP) algorithm that utilizes a sliding window filter of the most recent noisy aggregate observations along with encoded information from discarded observations. Our algorithm is built upon the recently proposed multi-marginal optimal transport based SBP algorithm that leverages standard belief propagation and Sinkhorn algorithm to solve inference problems from aggregate data. We demonstrate the performance of our algorithm on applications such as inferring population flow from aggregate observations.

Multi-marginal optimal transport and probabilistic graphical models

We study multi-marginal optimal transport problems from a probabilistic graphical model perspective. We point out an elegant connection between the two when the underlying cost for optimal transport allows a graph structure. In particular, an entropy regularized multi-marginal optimal transport is equivalent to a Bayesian marginal inference problem for probabilistic graphical models with the additional requirement that some of the marginal distributions are specified. This relation on the one hand extends the optimal transport as well as the probabilistic graphical model theories, and on the other hand leads to fast algorithms for multi-marginal optimal transport by leveraging the well-developed algorithms in Bayesian inference. Several numerical examples are provided to highlight the results.

Inference with Aggregate Data: An Optimal Transport Approach

We consider inference problems over probabilistic graphical models with aggregate data. In particular, we propose a new efficient belief propagation type algorithm over tree-structured graphs with polynomial computational complexity as well as a global convergence guarantee. This is in contrast to previous methods that either exhibit prohibitive complexity as the population grows or do not guarantee convergence. Our method is based on optimal transport, or more specifically, multi-marginal optimal transport theory. In particular, the inference problem with aggregate observations we consider in this paper can be seen as a structured multi-marginal optimal transport problem, where the cost function decomposes according to the underlying graph. Consequently, the celebrated Sinkhorn algorithm for multi-marginal optimal transport can be leveraged, together with the standard belief propagation algorithm to establish an efficient inference scheme. We demonstrate the performance of our algorithm on applications such as inferring population flow from aggregate observations.