Program Evaluation with Remotely Sensed Outcomes

While traditional program evaluations typically rely on surveys to measure outcomes, certain economic outcomes such as living standards or environmental quality may be infeasible or costly to collect. As a result, recent empirical work estimates treatment effects using remotely sensed variables (RSVs), such mobile phone activity or satellite images, instead of ground-truth outcome measurements. Common practice predicts the economic outcome from the RSV, using an auxiliary sample of labeled RSVs, and then uses such predictions as the outcome in the experiment. We prove that this approach leads to biased estimates of treatment effects when the RSV is a post-outcome variable. We nonparametrically identify the treatment effect, using an assumption that reflects the logic of recent empirical research: the conditional distribution of the RSV remains stable across both samples, given the outcome and treatment. Our results do not require researchers to know or consistently estimate the relationship between the RSV, outcome, and treatment, which is typically mis-specified with unstructured data. We form a representation of the RSV for downstream causal inference by predicting the outcome and predicting the treatment, with better predictions leading to more precise causal estimates. We re-evaluate the efficacy of a large-scale public program in India, showing that the program's measured effects on local consumption and poverty can be replicated using satellite

Provably Adaptive Average Reward Reinforcement Learning for Metric Spaces

We study infinite-horizon average-reward reinforcement learning (RL) for Lipschitz MDPs and develop an algorithm ZoRL that discretizes the state-action space adaptively and zooms into promising regions of the state-action space. We show that its regret can be bounded as $\mathcal{\tilde{O}}\big(T^{1 - d_{\text{eff.}}^{-1}}\big)$, where $d_{\text{eff.}} = 2d_\mathcal{S} + d_z + 3$, $d_\mathcal{S}$ is the dimension of the state space, and $d_z$ is the zooming dimension. $d_z$ is a problem-dependent quantity, which allows us to conclude that if MDP is benign, then its regret will be small. We note that the existing notion of zooming dimension for average reward RL is defined in terms of policy coverings, and hence it can be huge when the policy class is rich even though the underlying MDP is simple, so that the regret upper bound is nearly $O(T)$. The zooming dimension proposed in the current work is bounded above by $d$, the dimension of the state-action space, and hence is truly adaptive, i.e., shows how to capture adaptivity gains for infinite-horizon average-reward RL. ZoRL outperforms other state-of-the-art algorithms in experiments; thereby demonstrating the gains arising due to adaptivity.

Latent Representation Learning for Multimodal Brain Activity Translation

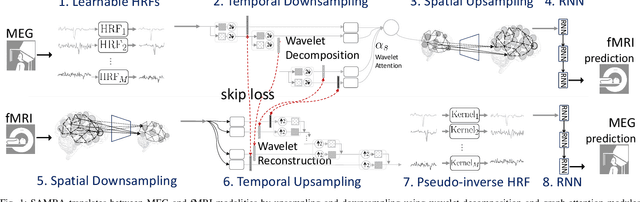
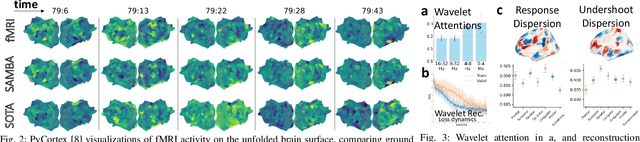
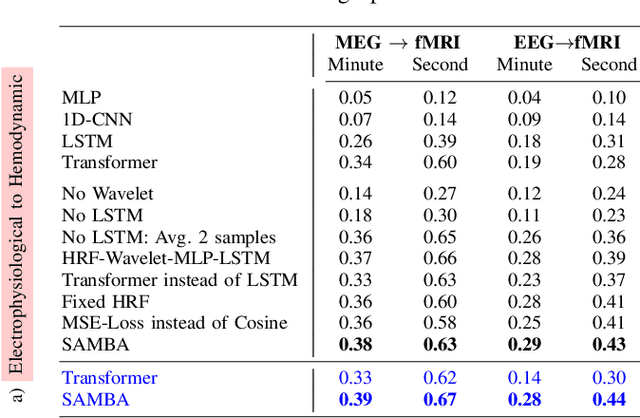
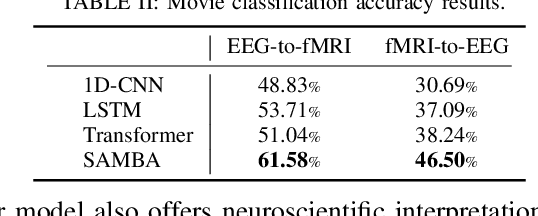
Neuroscience employs diverse neuroimaging techniques, each offering distinct insights into brain activity, from electrophysiological recordings such as EEG, which have high temporal resolution, to hemodynamic modalities such as fMRI, which have increased spatial precision. However, integrating these heterogeneous data sources remains a challenge, which limits a comprehensive understanding of brain function. We present the Spatiotemporal Alignment of Multimodal Brain Activity (SAMBA) framework, which bridges the spatial and temporal resolution gaps across modalities by learning a unified latent space free of modality-specific biases. SAMBA introduces a novel attention-based wavelet decomposition for spectral filtering of electrophysiological recordings, graph attention networks to model functional connectivity between functional brain units, and recurrent layers to capture temporal autocorrelations in brain signal. We show that the training of SAMBA, aside from achieving translation, also learns a rich representation of brain information processing. We showcase this classify external stimuli driving brain activity from the representation learned in hidden layers of SAMBA, paving the way for broad downstream applications in neuroscience research and clinical contexts.

Downstream bias mitigation is all you need

The advent of transformer-based architectures and large language models (LLMs) have significantly advanced the performance of natural language processing (NLP) models. Since these LLMs are trained on huge corpuses of data from the web and other sources, there has been a major concern about harmful prejudices that may potentially be transferred from the data. In many applications, these pre-trained LLMs are fine-tuned on task specific datasets, which can further contribute to biases. This paper studies the extent of biases absorbed by LLMs during pre-training as well as task-specific behaviour after fine-tuning. We found that controlled interventions on pre-trained LLMs, prior to fine-tuning, have minimal effect on lowering biases in classifiers. However, the biases present in domain-specific datasets play a much bigger role, and hence mitigating them at this stage has a bigger impact. While pre-training does matter, but after the model has been pre-trained, even slight changes to co-occurrence rates in the fine-tuning dataset has a significant effect on the bias of the model.

Automatic Generation of Behavioral Test Cases For Natural Language Processing Using Clustering and Prompting

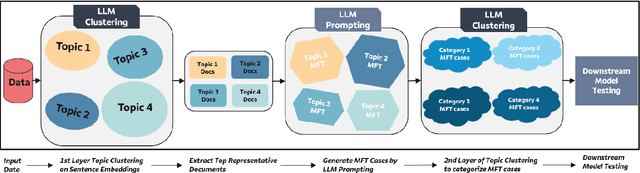
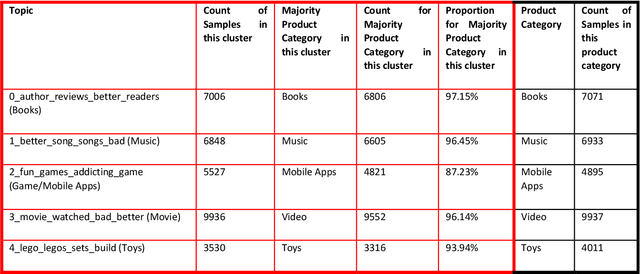
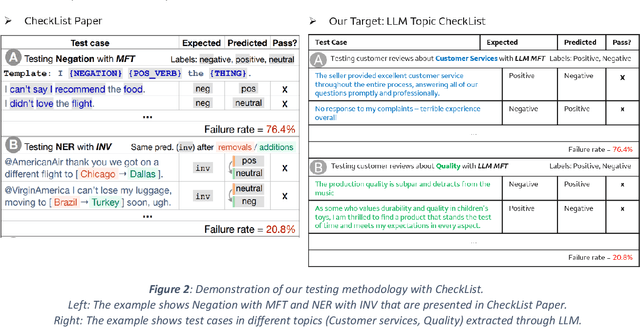
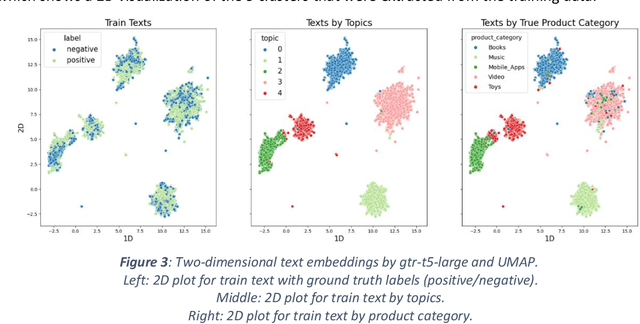
Recent work in behavioral testing for natural language processing (NLP) models, such as Checklist, is inspired by related paradigms in software engineering testing. They allow evaluation of general linguistic capabilities and domain understanding, hence can help evaluate conceptual soundness and identify model weaknesses. However, a major challenge is the creation of test cases. The current packages rely on semi-automated approach using manual development which requires domain expertise and can be time consuming. This paper introduces an automated approach to develop test cases by exploiting the power of large language models and statistical techniques. It clusters the text representations to carefully construct meaningful groups and then apply prompting techniques to automatically generate Minimal Functionality Tests (MFT). The well-known Amazon Reviews corpus is used to demonstrate our approach. We analyze the behavioral test profiles across four different classification algorithms and discuss the limitations and strengths of those models.

Adaptive Discretization-based Non-Episodic Reinforcement Learning in Metric Spaces

We study non-episodic Reinforcement Learning for Lipschitz MDPs in which state-action space is a metric space, and the transition kernel and rewards are Lipschitz functions. We develop computationally efficient UCB-based algorithm, $\textit{ZoRL-}\epsilon$ that adaptively discretizes the state-action space and show that their regret as compared with $\epsilon$-optimal policy is bounded as $\mathcal{O}(\epsilon^{-(2 d_\mathcal{S} + d^\epsilon_z + 1)}\log{(T)})$, where $d^\epsilon_z$ is the $\epsilon$-zooming dimension. In contrast, if one uses the vanilla $\textit{UCRL-}2$ on a fixed discretization of the MDP, the regret w.r.t. a $\epsilon$-optimal policy scales as $\mathcal{O}(\epsilon^{-(2 d_\mathcal{S} + d + 1)}\log{(T)})$ so that the adaptivity gains are huge when $d^\epsilon_z \ll d$. Note that the absolute regret of any 'uniformly good' algorithm for a large family of continuous MDPs asymptotically scales as at least $\Omega(\log{(T)})$. Though adaptive discretization has been shown to yield $\mathcal{\tilde{O}}(H^{2.5}K^\frac{d_z + 1}{d_z + 2})$ regret in episodic RL, an attempt to extend this to the non-episodic case by employing constant duration episodes whose duration increases with $T$, is futile since $d_z \to d$ as $T \to \infty$. The current work shows how to obtain adaptivity gains for non-episodic RL. The theoretical results are supported by simulations on two systems where the performance of $\textit{ZoRL-}\epsilon$ is compared with that of '$\textit{UCRL-C}$,' the fixed discretization-based extension of $\textit{UCRL-}2$ for systems with continuous state-action spaces.

On Learning for Ambiguous Chance Constrained Problems

We study chance constrained optimization problems $\min_x f(x)$ s.t. $P(\left\{ \theta: g(x,\theta)\le 0 \right\})\ge 1-\epsilon$ where $\epsilon\in (0,1)$ is the violation probability, when the distribution $P$ is not known to the decision maker (DM). When the DM has access to a set of distributions $\mathcal{U}$ such that $P$ is contained in $\mathcal{U}$, then the problem is known as the ambiguous chance-constrained problem \cite{erdougan2006ambiguous}. We study ambiguous chance-constrained problem for the case when $\mathcal{U}$ is of the form $\left\{\mu:\frac{\mu (y)}{\nu(y)}\leq C, \forall y\in\Theta, \mu(y)\ge 0\right\}$, where $\nu$ is a ``reference distribution.'' We show that in this case the original problem can be ``well-approximated'' by a sampled problem in which $N$ i.i.d. samples of $\theta$ are drawn from $\nu$, and the original constraint is replaced with $g(x,\theta_i)\le 0,~i=1,2,\ldots,N$. We also derive the sample complexity associated with this approximation, i.e., for $\epsilon,\delta>0$ the number of samples which must be drawn from $\nu$ so that with a probability greater than $1-\delta$ (over the randomness of $\nu$), the solution obtained by solving the sampled program yields an $\epsilon$-feasible solution for the original chance constrained problem.

Related Rhythms: Recommendation System To Discover Music You May Like

Machine Learning models are being utilized extensively to drive recommender systems, which is a widely explored topic today. This is especially true of the music industry, where we are witnessing a surge in growth. Besides a large chunk of active users, these systems are fueled by massive amounts of data. These large-scale systems yield applications that aim to provide a better user experience and to keep customers actively engaged. In this paper, a distributed Machine Learning (ML) pipeline is delineated, which is capable of taking a subset of songs as input and producing a new subset of songs identified as being similar to the inputted subset. The publicly accessible Million Songs Dataset (MSD) enables researchers to develop and explore reasonably efficient systems for audio track analysis and recommendations, without having to access a commercialized music platform. The objective of the proposed application is to leverage an ML system trained to optimally recommend songs that a user might like.

Finite Time Regret Bounds for Minimum Variance Control of Autoregressive Systems with Exogenous Inputs

Minimum variance controllers have been employed in a wide-range of industrial applications. A key challenge experienced by many adaptive controllers is their poor empirical performance in the initial stages of learning. In this paper, we address the problem of initializing them so that they provide acceptable transients, and also provide an accompanying finite-time regret analysis, for adaptive minimum variance control of an auto-regressive system with exogenous inputs (ARX). Following [3], we consider a modified version of the Certainty Equivalence (CE) adaptive controller, which we call PIECE, that utilizes probing inputs for exploration. We show that it has a $C \log T$ bound on the regret after $T$ time-steps for bounded noise, and $C\log^2 T$ in the case of sub-Gaussian noise. The simulation results demonstrate the advantage of PIECE over the algorithm proposed in [3] as well as the standard Certainty Equivalence controller especially in the initial learning phase. To the best of our knowledge, this is the first work that provides finite-time regret bounds for an adaptive minimum variance controller.

Kernel Ridge Regression Inference

We provide uniform confidence bands for kernel ridge regression (KRR), with finite sample guarantees. KRR is ubiquitous, yet--to our knowledge--this paper supplies the first exact, uniform confidence bands for KRR in the non-parametric regime where the regularization parameter $\lambda$ converges to 0, for general data distributions. Our proposed uniform confidence band is based on a new, symmetrized multiplier bootstrap procedure with a closed form solution, which allows for valid uncertainty quantification without assumptions on the bias. To justify the procedure, we derive non-asymptotic, uniform Gaussian and bootstrap couplings for partial sums in a reproducing kernel Hilbert space (RKHS) with bounded kernel. Our results imply strong approximation for empirical processes indexed by the RKHS unit ball, with sharp, logarithmic dependence on the covering number.