STAGED: A Multi-Agent Neural Network for Learning Cellular Interaction Dynamics

The advent of single-cell technology has significantly improved our understanding of cellular states and subpopulations in various tissues under normal and diseased conditions by employing data-driven approaches such as clustering and trajectory inference. However, these methods consider cells as independent data points of population distributions. With spatial transcriptomics, we can represent cellular organization, along with dynamic cell-cell interactions that lead to changes in cell state. Still, key computational advances are necessary to enable the data-driven learning of such complex interactive cellular dynamics. While agent-based modeling (ABM) provides a powerful framework, traditional approaches rely on handcrafted rules derived from domain knowledge rather than data-driven approaches. To address this, we introduce Spatio Temporal Agent-Based Graph Evolution Dynamics(STAGED) integrating ABM with deep learning to model intercellular communication, and its effect on the intracellular gene regulatory network. Using graph ODE networks (GDEs) with shared weights per cell type, our approach represents genes as vertices and interactions as directed edges, dynamically learning their strengths through a designed attention mechanism. Trained to match continuous trajectories of simulated as well as inferred trajectories from spatial transcriptomics data, the model captures both intercellular and intracellular interactions, enabling a more adaptive and accurate representation of cellular dynamics.

HiPoNet: A Topology-Preserving Multi-View Neural Network For High Dimensional Point Cloud and Single-Cell Data

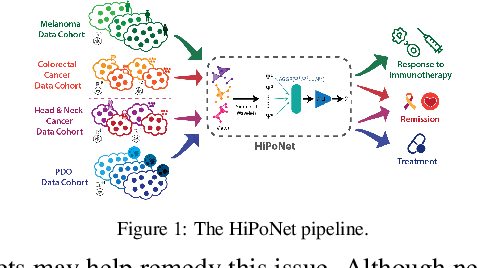
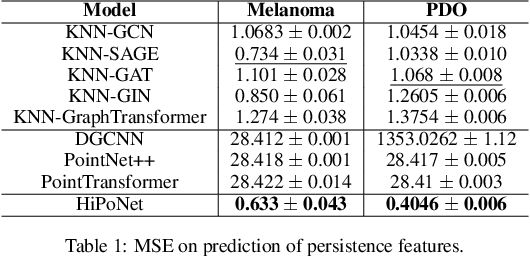
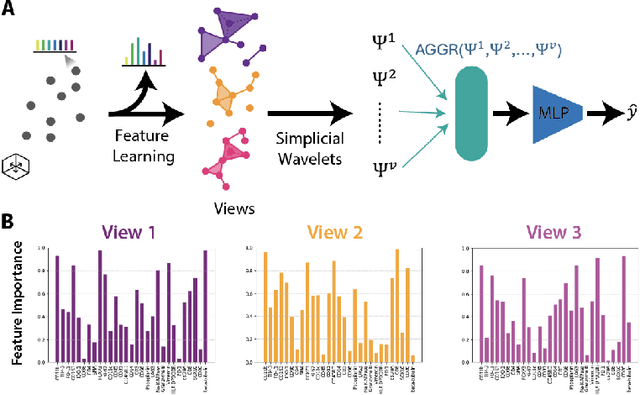
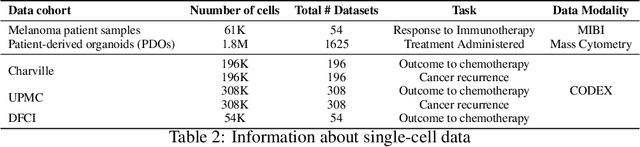
In this paper, we propose HiPoNet, an end-to-end differentiable neural network for regression, classification, and representation learning on high-dimensional point clouds. Single-cell data can have high dimensionality exceeding the capabilities of existing methods point cloud tailored for 3D data. Moreover, modern single-cell and spatial experiments now yield entire cohorts of datasets (i.e. one on every patient), necessitating models that can process large, high-dimensional point clouds at scale. Most current approaches build a single nearest-neighbor graph, discarding important geometric information. In contrast, HiPoNet forms higher-order simplicial complexes through learnable feature reweighting, generating multiple data views that disentangle distinct biological processes. It then employs simplicial wavelet transforms to extract multi-scale features - capturing both local and global topology. We empirically show that these components preserve topological information in the learned representations, and that HiPoNet significantly outperforms state-of-the-art point-cloud and graph-based models on single cell. We also show an application of HiPoNet on spatial transcriptomics datasets using spatial co-ordinates as one of the views. Overall, HiPoNet offers a robust and scalable solution for high-dimensional data analysis.

Principal Curvatures Estimation with Applications to Single Cell Data

The rapidly growing field of single-cell transcriptomic sequencing (scRNAseq) presents challenges for data analysis due to its massive datasets. A common method in manifold learning consists in hypothesizing that datasets lie on a lower dimensional manifold. This allows to study the geometry of point clouds by extracting meaningful descriptors like curvature. In this work, we will present Adaptive Local PCA (AdaL-PCA), a data-driven method for accurately estimating various notions of intrinsic curvature on data manifolds, in particular principal curvatures for surfaces. The model relies on local PCA to estimate the tangent spaces. The evaluation of AdaL-PCA on sampled surfaces shows state-of-the-art results. Combined with a PHATE embedding, the model applied to single-cell RNA sequencing data allows us to identify key variations in the cellular differentiation.

Exploring the Manifold of Neural Networks Using Diffusion Geometry

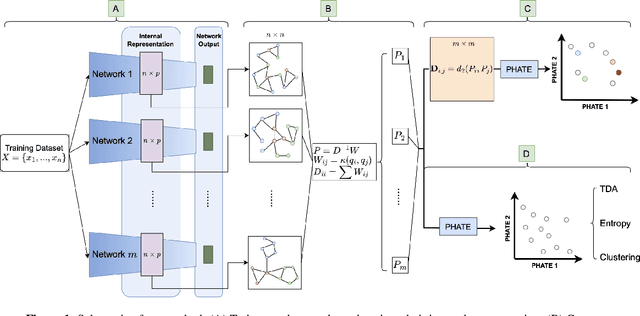
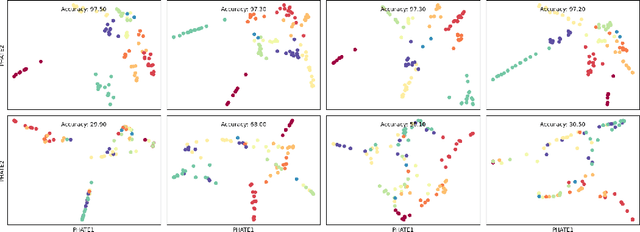
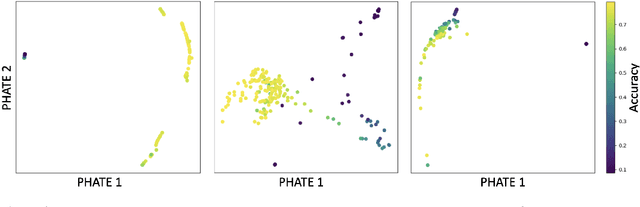
Drawing motivation from the manifold hypothesis, which posits that most high-dimensional data lies on or near low-dimensional manifolds, we apply manifold learning to the space of neural networks. We learn manifolds where datapoints are neural networks by introducing a distance between the hidden layer representations of the neural networks. These distances are then fed to the non-linear dimensionality reduction algorithm PHATE to create a manifold of neural networks. We characterize this manifold using features of the representation, including class separation, hierarchical cluster structure, spectral entropy, and topological structure. Our analysis reveals that high-performing networks cluster together in the manifold, displaying consistent embedding patterns across all these features. Finally, we demonstrate the utility of this approach for guiding hyperparameter optimization and neural architecture search by sampling from the manifold.

ProtSCAPE: Mapping the landscape of protein conformations in molecular dynamics

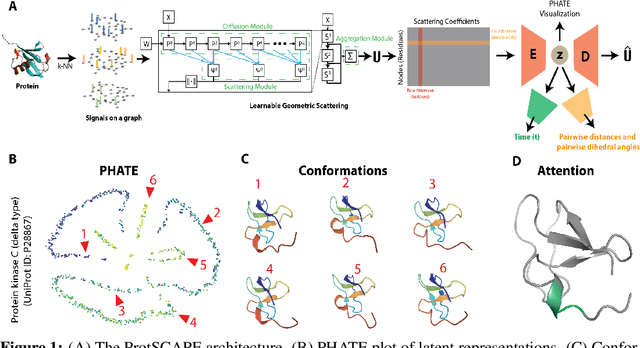
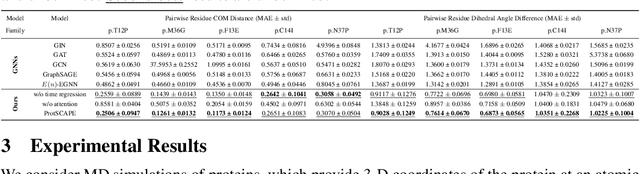
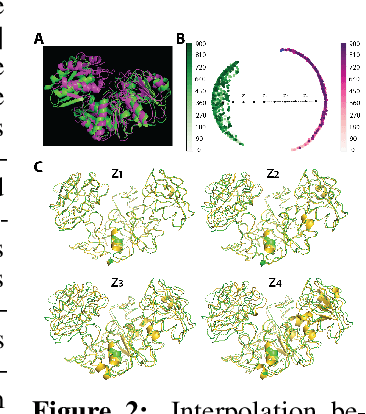
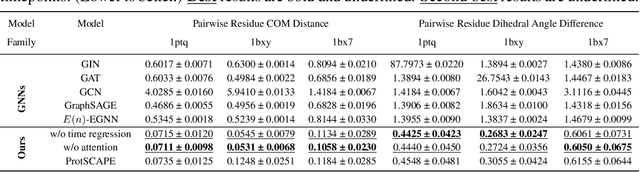
Understanding the dynamic nature of protein structures is essential for comprehending their biological functions. While significant progress has been made in predicting static folded structures, modeling protein motions on microsecond to millisecond scales remains challenging. To address these challenges, we introduce a novel deep learning architecture, Protein Transformer with Scattering, Attention, and Positional Embedding (ProtSCAPE), which leverages the geometric scattering transform alongside transformer-based attention mechanisms to capture protein dynamics from molecular dynamics (MD) simulations. ProtSCAPE utilizes the multi-scale nature of the geometric scattering transform to extract features from protein structures conceptualized as graphs and integrates these features with dual attention structures that focus on residues and amino acid signals, generating latent representations of protein trajectories. Furthermore, ProtSCAPE incorporates a regression head to enforce temporally coherent latent representations.

Latent Representation Learning for Multimodal Brain Activity Translation

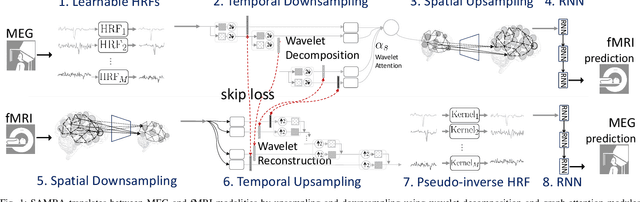
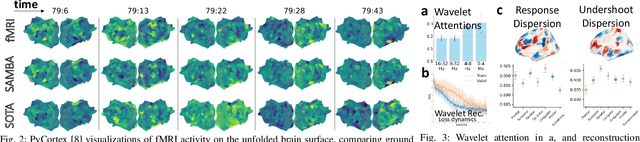
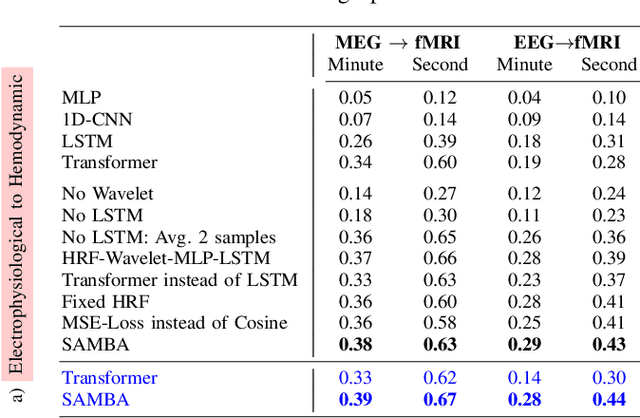
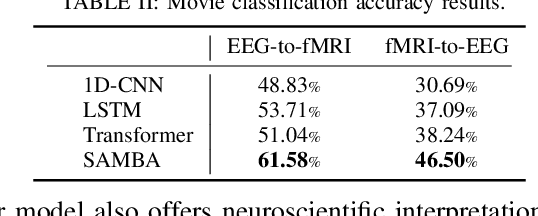
Neuroscience employs diverse neuroimaging techniques, each offering distinct insights into brain activity, from electrophysiological recordings such as EEG, which have high temporal resolution, to hemodynamic modalities such as fMRI, which have increased spatial precision. However, integrating these heterogeneous data sources remains a challenge, which limits a comprehensive understanding of brain function. We present the Spatiotemporal Alignment of Multimodal Brain Activity (SAMBA) framework, which bridges the spatial and temporal resolution gaps across modalities by learning a unified latent space free of modality-specific biases. SAMBA introduces a novel attention-based wavelet decomposition for spectral filtering of electrophysiological recordings, graph attention networks to model functional connectivity between functional brain units, and recurrent layers to capture temporal autocorrelations in brain signal. We show that the training of SAMBA, aside from achieving translation, also learns a rich representation of brain information processing. We showcase this classify external stimuli driving brain activity from the representation learned in hidden layers of SAMBA, paving the way for broad downstream applications in neuroscience research and clinical contexts.

Graph topological property recovery with heat and wave dynamics-based features on graphs

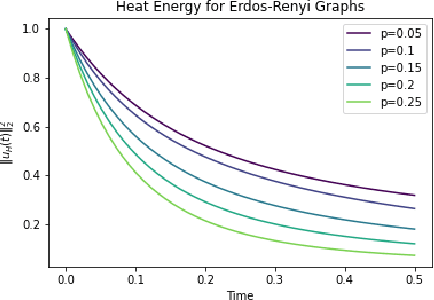
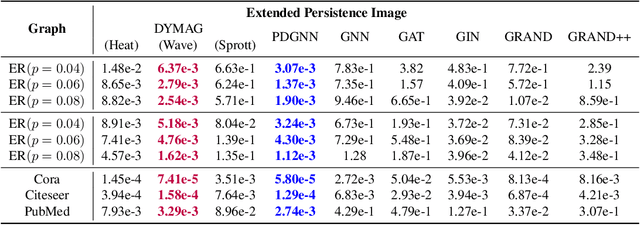
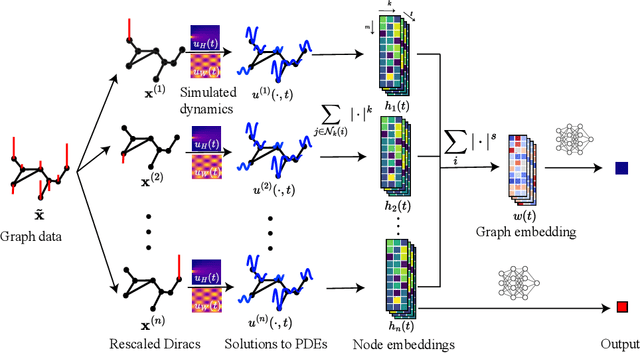
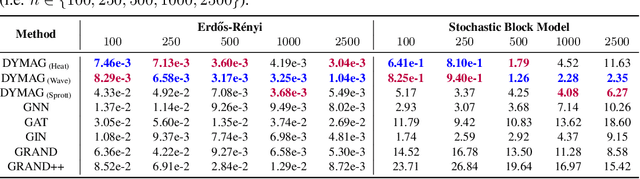
In this paper, we propose Graph Differential Equation Network (GDeNet), an approach that harnesses the expressive power of solutions to PDEs on a graph to obtain continuous node- and graph-level representations for various downstream tasks. We derive theoretical results connecting the dynamics of heat and wave equations to the spectral properties of the graph and to the behavior of continuous-time random walks on graphs. We demonstrate experimentally that these dynamics are able to capture salient aspects of graph geometry and topology by recovering generating parameters of random graphs, Ricci curvature, and persistent homology. Furthermore, we demonstrate the superior performance of GDeNet on real-world datasets including citation graphs, drug-like molecules, and proteins.

A Flow Artist for High-Dimensional Cellular Data

We consider the problem of embedding point cloud data sampled from an underlying manifold with an associated flow or velocity. Such data arises in many contexts where static snapshots of dynamic entities are measured, including in high-throughput biology such as single-cell transcriptomics. Existing embedding techniques either do not utilize velocity information or embed the coordinates and velocities independently, i.e., they either impose velocities on top of an existing point embedding or embed points within a prescribed vector field. Here we present FlowArtist, a neural network that embeds points while jointly learning a vector field around the points. The combination allows FlowArtist to better separate and visualize velocity-informed structures. Our results, on toy datasets and single-cell RNA velocity data, illustrate the value of utilizing coordinate and velocity information in tandem for embedding and visualizing high-dimensional data.

Inferring dynamic regulatory interaction graphs from time series data with perturbations

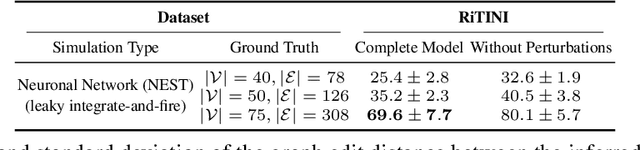
Complex systems are characterized by intricate interactions between entities that evolve dynamically over time. Accurate inference of these dynamic relationships is crucial for understanding and predicting system behavior. In this paper, we propose Regulatory Temporal Interaction Network Inference (RiTINI) for inferring time-varying interaction graphs in complex systems using a novel combination of space-and-time graph attentions and graph neural ordinary differential equations (ODEs). RiTINI leverages time-lapse signals on a graph prior, as well as perturbations of signals at various nodes in order to effectively capture the dynamics of the underlying system. This approach is distinct from traditional causal inference networks, which are limited to inferring acyclic and static graphs. In contrast, RiTINI can infer cyclic, directed, and time-varying graphs, providing a more comprehensive and accurate representation of complex systems. The graph attention mechanism in RiTINI allows the model to adaptively focus on the most relevant interactions in time and space, while the graph neural ODEs enable continuous-time modeling of the system's dynamics. We evaluate RiTINI's performance on various simulated and real-world datasets, demonstrating its state-of-the-art capability in inferring interaction graphs compared to previous methods.

Learnable Filters for Geometric Scattering Modules

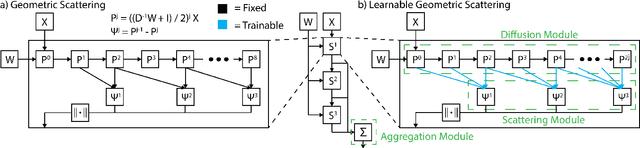
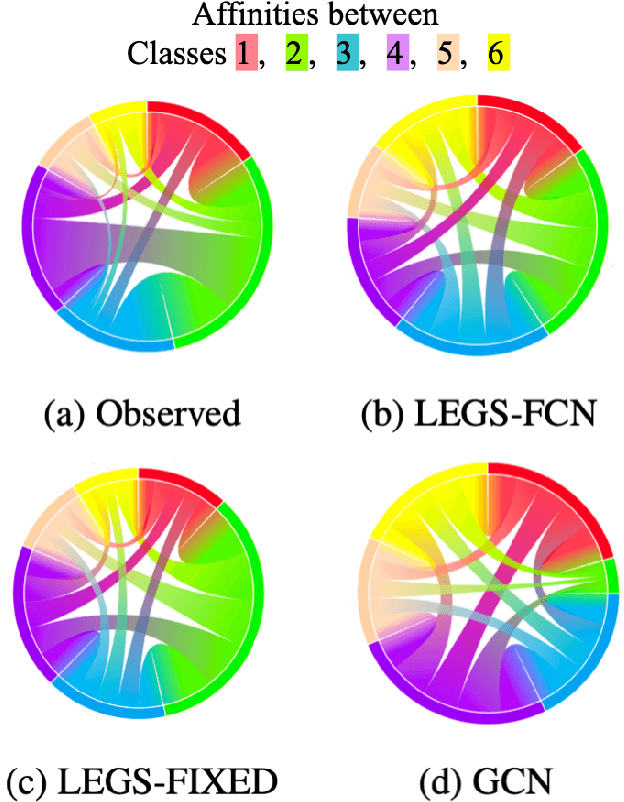
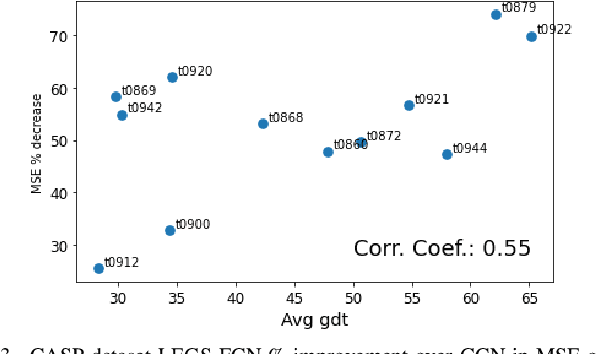
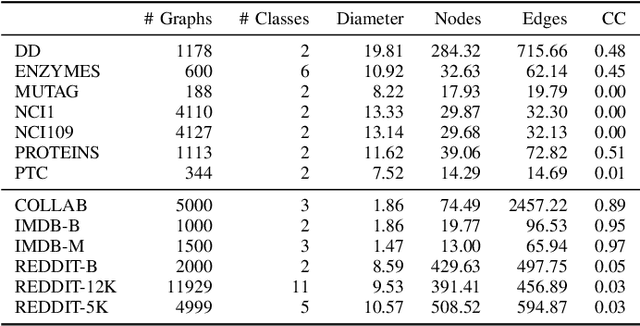
We propose a new graph neural network (GNN) module, based on relaxations of recently proposed geometric scattering transforms, which consist of a cascade of graph wavelet filters. Our learnable geometric scattering (LEGS) module enables adaptive tuning of the wavelets to encourage band-pass features to emerge in learned representations. The incorporation of our LEGS-module in GNNs enables the learning of longer-range graph relations compared to many popular GNNs, which often rely on encoding graph structure via smoothness or similarity between neighbors. Further, its wavelet priors result in simplified architectures with significantly fewer learned parameters compared to competing GNNs. We demonstrate the predictive performance of LEGS-based networks on graph classification benchmarks, as well as the descriptive quality of their learned features in biochemical graph data exploration tasks. Our results show that LEGS-based networks match or outperforms popular GNNs, as well as the original geometric scattering construction, on many datasets, in particular in biochemical domains, while retaining certain mathematical properties of handcrafted (non-learned) geometric scattering.