Directed Scattering for Knowledge Graph-based Cellular Signaling Analysis

Directed graphs are a natural model for many phenomena, in particular scientific knowledge graphs such as molecular interaction or chemical reaction networks that define cellular signaling relationships. In these situations, source nodes typically have distinct biophysical properties from sinks. Due to their ordered and unidirectional relationships, many such networks also have hierarchical and multiscale structure. However, the majority of methods performing node- and edge-level tasks in machine learning do not take these properties into account, and thus have not been leveraged effectively for scientific tasks such as cellular signaling network inference. We propose a new framework called Directed Scattering Autoencoder (DSAE) which uses a directed version of a geometric scattering transform, combined with the non-linear dimensionality reduction properties of an autoencoder and the geometric properties of the hyperbolic space to learn latent hierarchies. We show this method outperforms numerous others on tasks such as embedding directed graphs and learning cellular signaling networks.

Inferring dynamic regulatory interaction graphs from time series data with perturbations

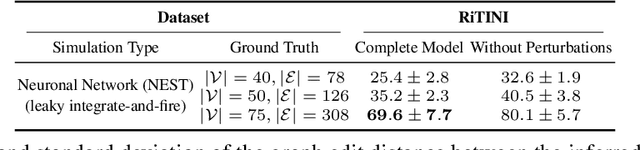
Complex systems are characterized by intricate interactions between entities that evolve dynamically over time. Accurate inference of these dynamic relationships is crucial for understanding and predicting system behavior. In this paper, we propose Regulatory Temporal Interaction Network Inference (RiTINI) for inferring time-varying interaction graphs in complex systems using a novel combination of space-and-time graph attentions and graph neural ordinary differential equations (ODEs). RiTINI leverages time-lapse signals on a graph prior, as well as perturbations of signals at various nodes in order to effectively capture the dynamics of the underlying system. This approach is distinct from traditional causal inference networks, which are limited to inferring acyclic and static graphs. In contrast, RiTINI can infer cyclic, directed, and time-varying graphs, providing a more comprehensive and accurate representation of complex systems. The graph attention mechanism in RiTINI allows the model to adaptively focus on the most relevant interactions in time and space, while the graph neural ODEs enable continuous-time modeling of the system's dynamics. We evaluate RiTINI's performance on various simulated and real-world datasets, demonstrating its state-of-the-art capability in inferring interaction graphs compared to previous methods.

Graph Fourier MMD for Signals on Graphs

While numerous methods have been proposed for computing distances between probability distributions in Euclidean space, relatively little attention has been given to computing such distances for distributions on graphs. However, there has been a marked increase in data that either lies on graph (such as protein interaction networks) or can be modeled as a graph (single cell data), particularly in the biomedical sciences. Thus, it becomes important to find ways to compare signals defined on such graphs. Here, we propose Graph Fourier MMD (GFMMD), a novel distance between distributions and signals on graphs. GFMMD is defined via an optimal witness function that is both smooth on the graph and maximizes difference in expectation between the pair of distributions on the graph. We find an analytical solution to this optimization problem as well as an embedding of distributions that results from this method. We also prove several properties of this method including scale invariance and applicability to disconnected graphs. We showcase it on graph benchmark datasets as well on single cell RNA-sequencing data analysis. In the latter, we use the GFMMD-based gene embeddings to find meaningful gene clusters. We also propose a novel type of score for gene selection called "gene localization score" which helps select genes for cellular state space characterization.