DC-W2S: Dual-Consensus Weak-to-Strong Training for Reliable Process Reward Modeling in Biological Reasoning

In scientific reasoning tasks, the veracity of the reasoning process is as critical as the final outcome. While Process Reward Models (PRMs) offer a solution to the coarse-grained supervision problems inherent in Outcome Reward Models (ORMs), their deployment is hindered by the prohibitive cost of obtaining expert-verified step-wise labels. This paper addresses the challenge of training reliable PRMs using abundant but noisy "weak" supervision. We argue that existing Weak-to-Strong Generalization (W2SG) theories lack prescriptive guidelines for selecting high-quality training signals from noisy data. To bridge this gap, we introduce the Dual-Consensus Weak-to-Strong (DC-W2S) framework. By intersecting Self-Consensus (SC) metrics among weak supervisors with Neighborhood-Consensus (NC) metrics in the embedding space, we stratify supervision signals into distinct reliability regimes. We then employ a curriculum of instance-level balanced sampling and label-level reliability-aware masking to guide the training process. We demonstrate that DC-W2S enables the training of robust PRMs for complex reasoning without exhaustive expert annotation, proving that strategic data curation is more effective than indiscriminate training on large-scale noisy datasets.

RAG-Enhanced Collaborative LLM Agents for Drug Discovery

Recent advances in large language models (LLMs) have shown great potential to accelerate drug discovery. However, the specialized nature of biochemical data often necessitates costly domain-specific fine-tuning, posing critical challenges. First, it hinders the application of more flexible general-purpose LLMs in cutting-edge drug discovery tasks. More importantly, it impedes the rapid integration of the vast amounts of scientific data continuously generated through experiments and research. To investigate these challenges, we propose CLADD, a retrieval-augmented generation (RAG)-empowered agentic system tailored to drug discovery tasks. Through the collaboration of multiple LLM agents, CLADD dynamically retrieves information from biomedical knowledge bases, contextualizes query molecules, and integrates relevant evidence to generate responses -- all without the need for domain-specific fine-tuning. Crucially, we tackle key obstacles in applying RAG workflows to biochemical data, including data heterogeneity, ambiguity, and multi-source integration. We demonstrate the flexibility and effectiveness of this framework across a variety of drug discovery tasks, showing that it outperforms general-purpose and domain-specific LLMs as well as traditional deep learning approaches.

Learning Predictive Checklists with Probabilistic Logic Programming

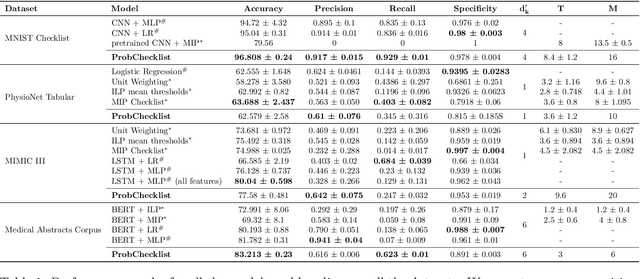
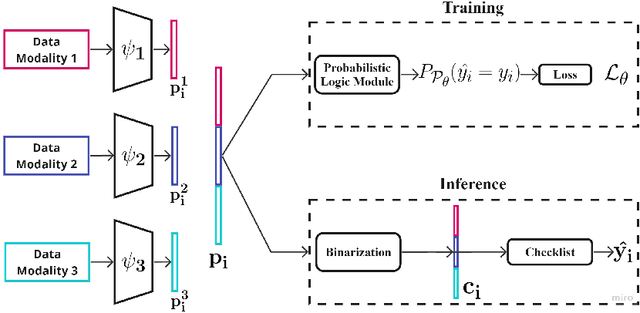
Checklists have been widely recognized as effective tools for completing complex tasks in a systematic manner. Although originally intended for use in procedural tasks, their interpretability and ease of use have led to their adoption for predictive tasks as well, including in clinical settings. However, designing checklists can be challenging, often requiring expert knowledge and manual rule design based on available data. Recent work has attempted to address this issue by using machine learning to automatically generate predictive checklists from data, although these approaches have been limited to Boolean data. We propose a novel method for learning predictive checklists from diverse data modalities, such as images and time series. Our approach relies on probabilistic logic programming, a learning paradigm that enables matching the discrete nature of checklist with continuous-valued data. We propose a regularization technique to tradeoff between the information captured in discrete concepts of continuous data and permit a tunable level of interpretability for the learned checklist concepts. We demonstrate that our method outperforms various explainable machine learning techniques on prediction tasks involving image sequences, time series, and clinical notes.

Convergence of Manifold Filter-Combine Networks

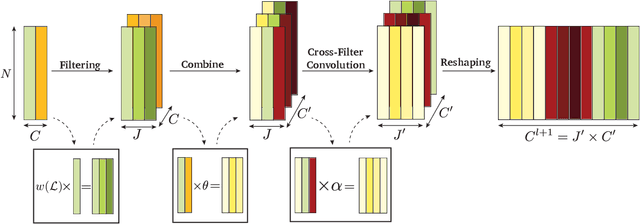
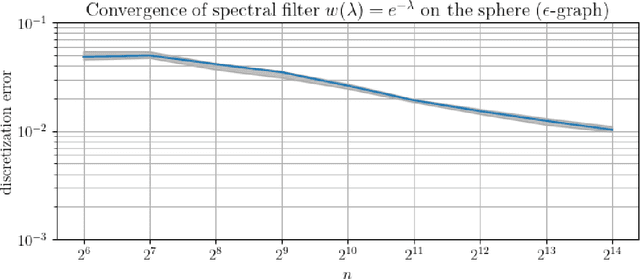
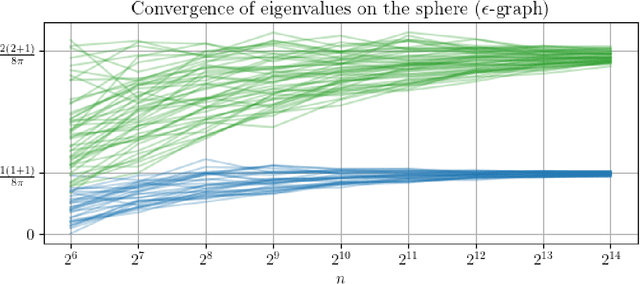
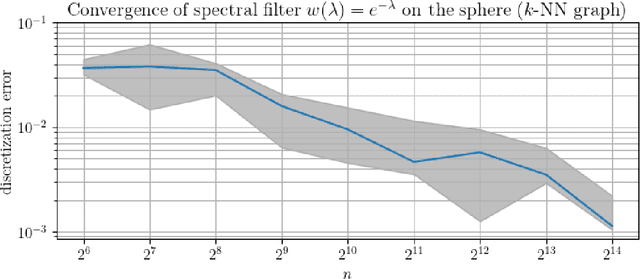
In order to better understand manifold neural networks (MNNs), we introduce Manifold Filter-Combine Networks (MFCNs). The filter-combine framework parallels the popular aggregate-combine paradigm for graph neural networks (GNNs) and naturally suggests many interesting families of MNNs which can be interpreted as the manifold analog of various popular GNNs. We then propose a method for implementing MFCNs on high-dimensional point clouds that relies on approximating the manifold by a sparse graph. We prove that our method is consistent in the sense that it converges to a continuum limit as the number of data points tends to infinity.

Atom-Level Optical Chemical Structure Recognition with Limited Supervision

Identifying the chemical structure from a graphical representation, or image, of a molecule is a challenging pattern recognition task that would greatly benefit drug development. Yet, existing methods for chemical structure recognition do not typically generalize well, and show diminished effectiveness when confronted with domains where data is sparse, or costly to generate, such as hand-drawn molecule images. To address this limitation, we propose a new chemical structure recognition tool that delivers state-of-the-art performance and can adapt to new domains with a limited number of data samples and supervision. Unlike previous approaches, our method provides atom-level localization, and can therefore segment the image into the different atoms and bonds. Our model is the first model to perform OCSR with atom-level entity detection with only SMILES supervision. Through rigorous and extensive benchmarking, we demonstrate the preeminence of our chemical structure recognition approach in terms of data efficiency, accuracy, and atom-level entity prediction.

Benchmarking Observational Studies with Experimental Data under Right-Censoring

Drawing causal inferences from observational studies (OS) requires unverifiable validity assumptions; however, one can falsify those assumptions by benchmarking the OS with experimental data from a randomized controlled trial (RCT). A major limitation of existing procedures is not accounting for censoring, despite the abundance of RCTs and OSes that report right-censored time-to-event outcomes. We consider two cases where censoring time (1) is independent of time-to-event and (2) depends on time-to-event the same way in OS and RCT. For the former, we adopt a censoring-doubly-robust signal for the conditional average treatment effect (CATE) to facilitate an equivalence test of CATEs in OS and RCT, which serves as a proxy for testing if the validity assumptions hold. For the latter, we show that the same test can still be used even though unbiased CATE estimation may not be possible. We verify the effectiveness of our censoring-aware tests via semi-synthetic experiments and analyze RCT and OS data from the Women's Health Initiative study.

BLIS-Net: Classifying and Analyzing Signals on Graphs

Graph neural networks (GNNs) have emerged as a powerful tool for tasks such as node classification and graph classification. However, much less work has been done on signal classification, where the data consists of many functions (referred to as signals) defined on the vertices of a single graph. These tasks require networks designed differently from those designed for traditional GNN tasks. Indeed, traditional GNNs rely on localized low-pass filters, and signals of interest may have intricate multi-frequency behavior and exhibit long range interactions. This motivates us to introduce the BLIS-Net (Bi-Lipschitz Scattering Net), a novel GNN that builds on the previously introduced geometric scattering transform. Our network is able to capture both local and global signal structure and is able to capture both low-frequency and high-frequency information. We make several crucial changes to the original geometric scattering architecture which we prove increase the ability of our network to capture information about the input signal and show that BLIS-Net achieves superior performance on both synthetic and real-world data sets based on traffic flow and fMRI data.

Manifold Filter-Combine Networks

We introduce a class of manifold neural networks (MNNs) that we call Manifold Filter-Combine Networks (MFCNs), that aims to further our understanding of MNNs, analogous to how the aggregate-combine framework helps with the understanding of graph neural networks (GNNs). This class includes a wide variety of subclasses that can be thought of as the manifold analog of various popular GNNs. We then consider a method, based on building a data-driven graph, for implementing such networks when one does not have global knowledge of the manifold, but merely has access to finitely many sample points. We provide sufficient conditions for the network to provably converge to its continuum limit as the number of sample points tends to infinity. Unlike previous work (which focused on specific graph constructions), our rate of convergence does not directly depend on the number of filters used. Moreover, it exhibits linear dependence on the depth of the network rather than the exponential dependence obtained previously. Additionally, we provide several examples of interesting subclasses of MFCNs and of the rates of convergence that are obtained under specific graph constructions.

Inferring dynamic regulatory interaction graphs from time series data with perturbations

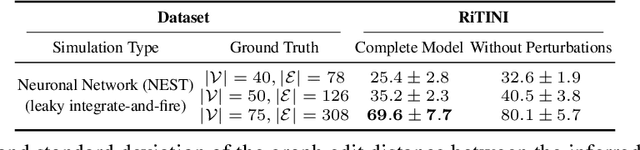
Complex systems are characterized by intricate interactions between entities that evolve dynamically over time. Accurate inference of these dynamic relationships is crucial for understanding and predicting system behavior. In this paper, we propose Regulatory Temporal Interaction Network Inference (RiTINI) for inferring time-varying interaction graphs in complex systems using a novel combination of space-and-time graph attentions and graph neural ordinary differential equations (ODEs). RiTINI leverages time-lapse signals on a graph prior, as well as perturbations of signals at various nodes in order to effectively capture the dynamics of the underlying system. This approach is distinct from traditional causal inference networks, which are limited to inferring acyclic and static graphs. In contrast, RiTINI can infer cyclic, directed, and time-varying graphs, providing a more comprehensive and accurate representation of complex systems. The graph attention mechanism in RiTINI allows the model to adaptively focus on the most relevant interactions in time and space, while the graph neural ODEs enable continuous-time modeling of the system's dynamics. We evaluate RiTINI's performance on various simulated and real-world datasets, demonstrating its state-of-the-art capability in inferring interaction graphs compared to previous methods.

A Heat Diffusion Perspective on Geodesic Preserving Dimensionality Reduction

Diffusion-based manifold learning methods have proven useful in representation learning and dimensionality reduction of modern high dimensional, high throughput, noisy datasets. Such datasets are especially present in fields like biology and physics. While it is thought that these methods preserve underlying manifold structure of data by learning a proxy for geodesic distances, no specific theoretical links have been established. Here, we establish such a link via results in Riemannian geometry explicitly connecting heat diffusion to manifold distances. In this process, we also formulate a more general heat kernel based manifold embedding method that we call heat geodesic embeddings. This novel perspective makes clearer the choices available in manifold learning and denoising. Results show that our method outperforms existing state of the art in preserving ground truth manifold distances, and preserving cluster structure in toy datasets. We also showcase our method on single cell RNA-sequencing datasets with both continuum and cluster structure, where our method enables interpolation of withheld timepoints of data. Finally, we show that parameters of our more general method can be configured to give results similar to PHATE (a state-of-the-art diffusion based manifold learning method) as well as SNE (an attraction/repulsion neighborhood based method that forms the basis of t-SNE).