Exploring the Manifold of Neural Networks Using Diffusion Geometry

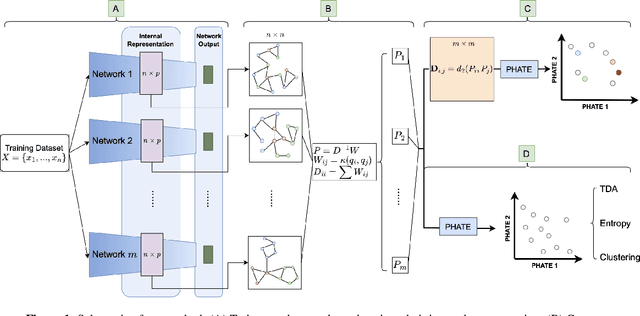
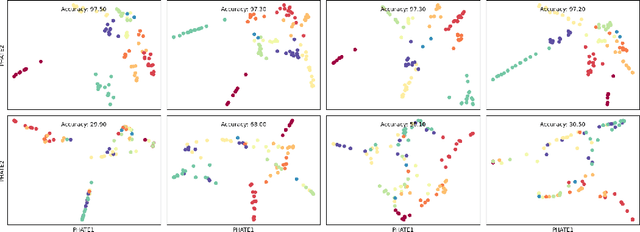
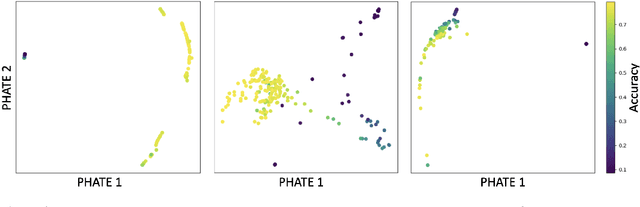
Drawing motivation from the manifold hypothesis, which posits that most high-dimensional data lies on or near low-dimensional manifolds, we apply manifold learning to the space of neural networks. We learn manifolds where datapoints are neural networks by introducing a distance between the hidden layer representations of the neural networks. These distances are then fed to the non-linear dimensionality reduction algorithm PHATE to create a manifold of neural networks. We characterize this manifold using features of the representation, including class separation, hierarchical cluster structure, spectral entropy, and topological structure. Our analysis reveals that high-performing networks cluster together in the manifold, displaying consistent embedding patterns across all these features. Finally, we demonstrate the utility of this approach for guiding hyperparameter optimization and neural architecture search by sampling from the manifold.

Geometry-Aware Generative Autoencoders for Warped Riemannian Metric Learning and Generative Modeling on Data Manifolds

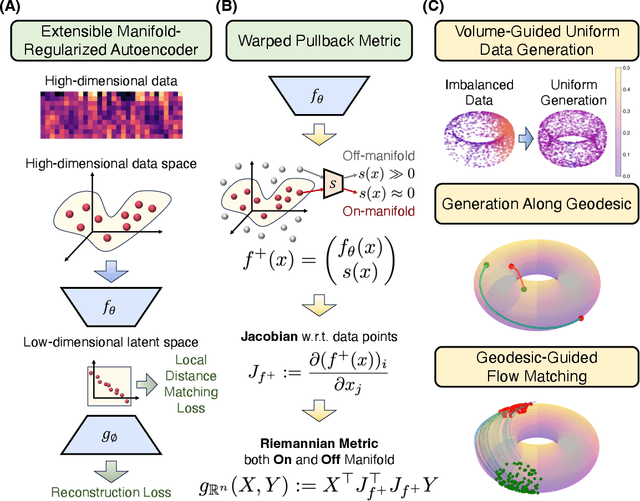
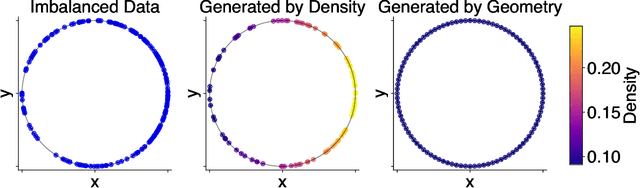
Rapid growth of high-dimensional datasets in fields such as single-cell RNA sequencing and spatial genomics has led to unprecedented opportunities for scientific discovery, but it also presents unique computational and statistical challenges. Traditional methods struggle with geometry-aware data generation, interpolation along meaningful trajectories, and transporting populations via feasible paths. To address these issues, we introduce Geometry-Aware Generative Autoencoder (GAGA), a novel framework that combines extensible manifold learning with generative modeling. GAGA constructs a neural network embedding space that respects the intrinsic geometries discovered by manifold learning and learns a novel warped Riemannian metric on the data space. This warped metric is derived from both the points on the data manifold and negative samples off the manifold, allowing it to characterize a meaningful geometry across the entire latent space. Using this metric, GAGA can uniformly sample points on the manifold, generate points along geodesics, and interpolate between populations across the learned manifold. GAGA shows competitive performance in simulated and real world datasets, including a 30% improvement over the state-of-the-art methods in single-cell population-level trajectory inference.

AdaFisher: Adaptive Second Order Optimization via Fisher Information

First-order optimization methods are currently the mainstream in training deep neural networks (DNNs). Optimizers like Adam incorporate limited curvature information by employing the diagonal matrix preconditioning of the stochastic gradient during the training. Despite their widespread, second-order optimization algorithms exhibit superior convergence properties compared to their first-order counterparts e.g. Adam and SGD. However, their practicality in training DNNs are still limited due to increased per-iteration computations and suboptimal accuracy compared to the first order methods. We present AdaFisher--an adaptive second-order optimizer that leverages a block-diagonal approximation to the Fisher information matrix for adaptive gradient preconditioning. AdaFisher aims to bridge the gap between enhanced convergence capabilities and computational efficiency in second-order optimization framework for training DNNs. Despite the slow pace of second-order optimizers, we showcase that AdaFisher can be reliably adopted for image classification, language modelling and stand out for its stability and robustness in hyperparameter tuning. We demonstrate that AdaFisher outperforms the SOTA optimizers in terms of both accuracy and convergence speed. Code available from \href{https://github.com/AtlasAnalyticsLab/AdaFisher}{https://github.com/AtlasAnalyticsLab/AdaFisher}

Graph topological property recovery with heat and wave dynamics-based features on graphs

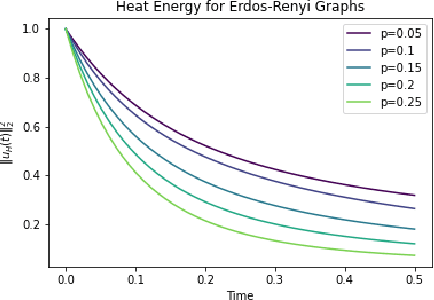
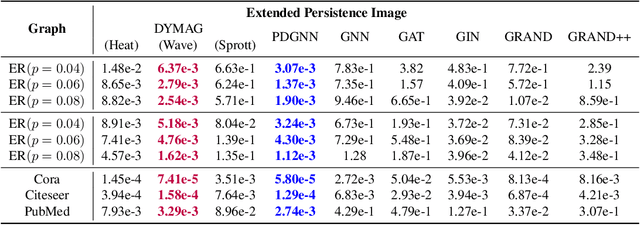
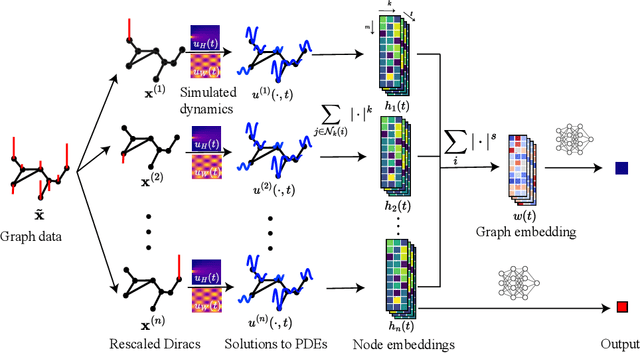
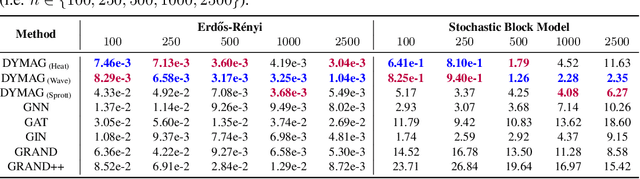
In this paper, we propose Graph Differential Equation Network (GDeNet), an approach that harnesses the expressive power of solutions to PDEs on a graph to obtain continuous node- and graph-level representations for various downstream tasks. We derive theoretical results connecting the dynamics of heat and wave equations to the spectral properties of the graph and to the behavior of continuous-time random walks on graphs. We demonstrate experimentally that these dynamics are able to capture salient aspects of graph geometry and topology by recovering generating parameters of random graphs, Ricci curvature, and persistent homology. Furthermore, we demonstrate the superior performance of GDeNet on real-world datasets including citation graphs, drug-like molecules, and proteins.

Simulation-free Schrödinger bridges via score and flow matching

We present simulation-free score and flow matching ([SF]$^2$M), a simulation-free objective for inferring stochastic dynamics given unpaired source and target samples drawn from arbitrary distributions. Our method generalizes both the score-matching loss used in the training of diffusion models and the recently proposed flow matching loss used in the training of continuous normalizing flows. [SF]$^2$M interprets continuous-time stochastic generative modeling as a Schr\"odinger bridge (SB) problem. It relies on static entropy-regularized optimal transport, or a minibatch approximation, to efficiently learn the SB without simulating the learned stochastic process. We find that [SF]$^2$M is more efficient and gives more accurate solutions to the SB problem than simulation-based methods from prior work. Finally, we apply [SF]$^2$M to the problem of learning cell dynamics from snapshot data. Notably, [SF]$^2$M is the first method to accurately model cell dynamics in high dimensions and can recover known gene regulatory networks from simulated data.

Neural FIM for learning Fisher Information Metrics from point cloud data

Although data diffusion embeddings are ubiquitous in unsupervised learning and have proven to be a viable technique for uncovering the underlying intrinsic geometry of data, diffusion embeddings are inherently limited due to their discrete nature. To this end, we propose neural FIM, a method for computing the Fisher information metric (FIM) from point cloud data - allowing for a continuous manifold model for the data. Neural FIM creates an extensible metric space from discrete point cloud data such that information from the metric can inform us of manifold characteristics such as volume and geodesics. We demonstrate Neural FIM's utility in selecting parameters for the PHATE visualization method as well as its ability to obtain information pertaining to local volume illuminating branching points and cluster centers embeddings of a toy dataset and two single-cell datasets of IPSC reprogramming and PBMCs (immune cells).

A Heat Diffusion Perspective on Geodesic Preserving Dimensionality Reduction

Diffusion-based manifold learning methods have proven useful in representation learning and dimensionality reduction of modern high dimensional, high throughput, noisy datasets. Such datasets are especially present in fields like biology and physics. While it is thought that these methods preserve underlying manifold structure of data by learning a proxy for geodesic distances, no specific theoretical links have been established. Here, we establish such a link via results in Riemannian geometry explicitly connecting heat diffusion to manifold distances. In this process, we also formulate a more general heat kernel based manifold embedding method that we call heat geodesic embeddings. This novel perspective makes clearer the choices available in manifold learning and denoising. Results show that our method outperforms existing state of the art in preserving ground truth manifold distances, and preserving cluster structure in toy datasets. We also showcase our method on single cell RNA-sequencing datasets with both continuum and cluster structure, where our method enables interpolation of withheld timepoints of data. Finally, we show that parameters of our more general method can be configured to give results similar to PHATE (a state-of-the-art diffusion based manifold learning method) as well as SNE (an attraction/repulsion neighborhood based method that forms the basis of t-SNE).

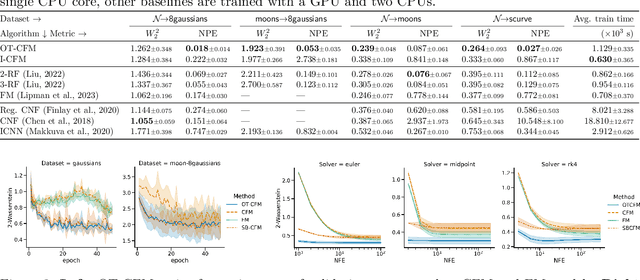
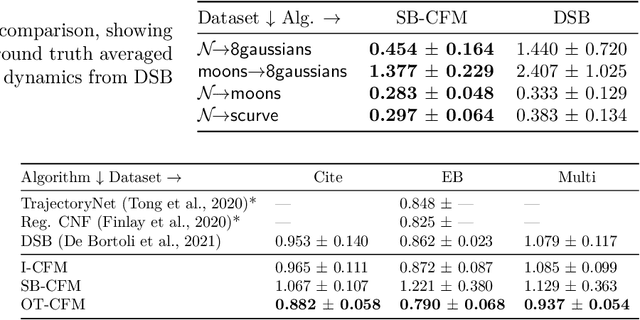
Conditional Flow Matching: Simulation-Free Dynamic Optimal Transport

Continuous normalizing flows (CNFs) are an attractive generative modeling technique, but they have thus far been held back by limitations in their simulation-based maximum likelihood training. In this paper, we introduce a new technique called conditional flow matching (CFM), a simulation-free training objective for CNFs. CFM features a stable regression objective like that used to train the stochastic flow in diffusion models but enjoys the efficient inference of deterministic flow models. In contrast to both diffusion models and prior CNF training algorithms, our CFM objective does not require the source distribution to be Gaussian or require evaluation of its density. Based on this new objective, we also introduce optimal transport CFM (OT-CFM), which creates simpler flows that are more stable to train and lead to faster inference, as evaluated in our experiments. Training CNFs with CFM improves results on a variety of conditional and unconditional generation tasks such as inferring single cell dynamics, unsupervised image translation, and Schr\"odinger bridge inference. Code is available at https://github.com/atong01/conditional-flow-matching .