Recursive Self-Aggregation Unlocks Deep Thinking in Large Language Models

Test-time scaling methods improve the capabilities of large language models (LLMs) by increasing the amount of compute used during inference to make a prediction. Inference-time compute can be scaled in parallel by choosing among multiple independent solutions or sequentially through self-refinement. We propose Recursive Self-Aggregation (RSA), a test-time scaling method inspired by evolutionary methods that combines the benefits of both parallel and sequential scaling. Each step of RSA refines a population of candidate reasoning chains through aggregation of subsets to yield a population of improved solutions, which are then used as the candidate pool for the next iteration. RSA exploits the rich information embedded in the reasoning chains -- not just the final answers -- and enables bootstrapping from partially correct intermediate steps within different chains of thought. Empirically, RSA delivers substantial performance gains with increasing compute budgets across diverse tasks, model families and sizes. Notably, RSA enables Qwen3-4B-Instruct-2507 to achieve competitive performance with larger reasoning models, including DeepSeek-R1 and o3-mini (high), while outperforming purely parallel and sequential scaling strategies across AIME-25, HMMT-25, Reasoning Gym, LiveCodeBench-v6, and SuperGPQA. We further demonstrate that training the model to combine solutions via a novel aggregation-aware reinforcement learning approach yields significant performance gains. Code available at https://github.com/HyperPotatoNeo/RSA.

Fast Flow-based Visuomotor Policies via Conditional Optimal Transport Couplings

Diffusion and flow matching policies have recently demonstrated remarkable performance in robotic applications by accurately capturing multimodal robot trajectory distributions. However, their computationally expensive inference, due to the numerical integration of an ODE or SDE, limits their applicability as real-time controllers for robots. We introduce a methodology that utilizes conditional Optimal Transport couplings between noise and samples to enforce straight solutions in the flow ODE for robot action generation tasks. We show that naively coupling noise and samples fails in conditional tasks and propose incorporating condition variables into the coupling process to improve few-step performance. The proposed few-step policy achieves a 4% higher success rate with a 10x speed-up compared to Diffusion Policy on a diverse set of simulation tasks. Moreover, it produces high-quality and diverse action trajectories within 1-2 steps on a set of real-world robot tasks. Our method also retains the same training complexity as Diffusion Policy and vanilla Flow Matching, in contrast to distillation-based approaches.

Solving Bayesian inverse problems with diffusion priors and off-policy RL

This paper presents a practical application of Relative Trajectory Balance (RTB), a recently introduced off-policy reinforcement learning (RL) objective that can asymptotically solve Bayesian inverse problems optimally. We extend the original work by using RTB to train conditional diffusion model posteriors from pretrained unconditional priors for challenging linear and non-linear inverse problems in vision, and science. We use the objective alongside techniques such as off-policy backtracking exploration to improve training. Importantly, our results show that existing training-free diffusion posterior methods struggle to perform effective posterior inference in latent space due to inherent biases.

Learning Decision Trees as Amortized Structure Inference

Building predictive models for tabular data presents fundamental challenges, notably in scaling consistently, i.e., more resources translating to better performance, and generalizing systematically beyond the training data distribution. Designing decision tree models remains especially challenging given the intractably large search space, and most existing methods rely on greedy heuristics, while deep learning inductive biases expect a temporal or spatial structure not naturally present in tabular data. We propose a hybrid amortized structure inference approach to learn predictive decision tree ensembles given data, formulating decision tree construction as a sequential planning problem. We train a deep reinforcement learning (GFlowNet) policy to solve this problem, yielding a generative model that samples decision trees from the Bayesian posterior. We show that our approach, DT-GFN, outperforms state-of-the-art decision tree and deep learning methods on standard classification benchmarks derived from real-world data, robustness to distribution shifts, and anomaly detection, all while yielding interpretable models with shorter description lengths. Samples from the trained DT-GFN model can be ensembled to construct a random forest, and we further show that the performance of scales consistently in ensemble size, yielding ensembles of predictors that continue to generalize systematically.

In-Context Parametric Inference: Point or Distribution Estimators?

Bayesian and frequentist inference are two fundamental paradigms in statistical estimation. Bayesian methods treat hypotheses as random variables, incorporating priors and updating beliefs via Bayes' theorem, whereas frequentist methods assume fixed but unknown hypotheses, relying on estimators like maximum likelihood. While extensive research has compared these approaches, the frequentist paradigm of obtaining point estimates has become predominant in deep learning, as Bayesian inference is challenging due to the computational complexity and the approximation gap of posterior estimation methods. However, a good understanding of trade-offs between the two approaches is lacking in the regime of amortized estimators, where in-context learners are trained to estimate either point values via maximum likelihood or maximum a posteriori estimation, or full posteriors using normalizing flows, score-based diffusion samplers, or diagonal Gaussian approximations, conditioned on observations. To help resolve this, we conduct a rigorous comparative analysis spanning diverse problem settings, from linear models to shallow neural networks, with a robust evaluation framework assessing both in-distribution and out-of-distribution generalization on tractable tasks. Our experiments indicate that amortized point estimators generally outperform posterior inference, though the latter remain competitive in some low-dimensional problems, and we further discuss why this might be the case.

Outsourced diffusion sampling: Efficient posterior inference in latent spaces of generative models

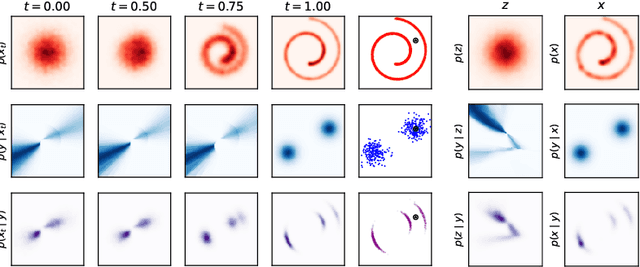
Any well-behaved generative model over a variable $\mathbf{x}$ can be expressed as a deterministic transformation of an exogenous ('outsourced') Gaussian noise variable $\mathbf{z}$: $\mathbf{x}=f_\theta(\mathbf{z})$. In such a model (e.g., a VAE, GAN, or continuous-time flow-based model), sampling of the target variable $\mathbf{x} \sim p_\theta(\mathbf{x})$ is straightforward, but sampling from a posterior distribution of the form $p(\mathbf{x}\mid\mathbf{y}) \propto p_\theta(\mathbf{x})r(\mathbf{x},\mathbf{y})$, where $r$ is a constraint function depending on an auxiliary variable $\mathbf{y}$, is generally intractable. We propose to amortize the cost of sampling from such posterior distributions with diffusion models that sample a distribution in the noise space ($\mathbf{z}$). These diffusion samplers are trained by reinforcement learning algorithms to enforce that the transformed samples $f_\theta(\mathbf{z})$ are distributed according to the posterior in the data space ($\mathbf{x}$). For many models and constraints of interest, the posterior in the noise space is smoother than the posterior in the data space, making it more amenable to such amortized inference. Our method enables conditional sampling under unconditional GAN, (H)VAE, and flow-based priors, comparing favorably both with current amortized and non-amortized inference methods. We demonstrate the proposed outsourced diffusion sampling in several experiments with large pretrained prior models: conditional image generation, reinforcement learning with human feedback, and protein structure generation.

From discrete-time policies to continuous-time diffusion samplers: Asymptotic equivalences and faster training

We study the problem of training neural stochastic differential equations, or diffusion models, to sample from a Boltzmann distribution without access to target samples. Existing methods for training such models enforce time-reversal of the generative and noising processes, using either differentiable simulation or off-policy reinforcement learning (RL). We prove equivalences between families of objectives in the limit of infinitesimal discretization steps, linking entropic RL methods (GFlowNets) with continuous-time objects (partial differential equations and path space measures). We further show that an appropriate choice of coarse time discretization during training allows greatly improved sample efficiency and the use of time-local objectives, achieving competitive performance on standard sampling benchmarks with reduced computational cost.

Mixtures of In-Context Learners

In-context learning (ICL) adapts LLMs by providing demonstrations without fine-tuning the model parameters; however, it does not differentiate between demonstrations and quadratically increases the complexity of Transformer LLMs, exhausting the memory. As a solution, we propose Mixtures of In-Context Learners (MoICL), a novel approach to treat subsets of demonstrations as experts and learn a weighting function to merge their output distributions based on a training set. In our experiments, we show performance improvements on 5 out of 7 classification datasets compared to a set of strong baselines (up to +13\% compared to ICL and LENS). Moreover, we enhance the Pareto frontier of ICL by reducing the inference time needed to achieve the same performance with fewer demonstrations. Finally, MoICL is more robust to out-of-domain (up to +11\%), imbalanced (up to +49\%), or noisy demonstrations (up to +38\%) or can filter these out from datasets. Overall, MoICL is a more expressive approach to learning from demonstrations without exhausting the context window or memory.

Action abstractions for amortized sampling

As trajectories sampled by policies used by reinforcement learning (RL) and generative flow networks (GFlowNets) grow longer, credit assignment and exploration become more challenging, and the long planning horizon hinders mode discovery and generalization. The challenge is particularly pronounced in entropy-seeking RL methods, such as generative flow networks, where the agent must learn to sample from a structured distribution and discover multiple high-reward states, each of which take many steps to reach. To tackle this challenge, we propose an approach to incorporate the discovery of action abstractions, or high-level actions, into the policy optimization process. Our approach involves iteratively extracting action subsequences commonly used across many high-reward trajectories and `chunking' them into a single action that is added to the action space. In empirical evaluation on synthetic and real-world environments, our approach demonstrates improved sample efficiency performance in discovering diverse high-reward objects, especially on harder exploration problems. We also observe that the abstracted high-order actions are interpretable, capturing the latent structure of the reward landscape of the action space. This work provides a cognitively motivated approach to action abstraction in RL and is the first demonstration of hierarchical planning in amortized sequential sampling.

Proof Flow: Preliminary Study on Generative Flow Network Language Model Tuning for Formal Reasoning

Reasoning is a fundamental substrate for solving novel and complex problems. Deliberate efforts in learning and developing frameworks around System 2 reasoning have made great strides, yet problems of sufficient complexity remain largely out of reach for open models. To address this gap, we examine the potential of Generative Flow Networks as a fine-tuning method for LLMs to unlock advanced reasoning capabilities. In this paper, we present a proof of concept in the domain of formal reasoning, specifically in the Neural Theorem Proving (NTP) setting, where proofs specified in a formal language such as Lean can be deterministically and objectively verified. Unlike classical reward-maximization reinforcement learning, which frequently over-exploits high-reward actions and fails to effectively explore the state space, GFlowNets have emerged as a promising approach for sampling compositional objects, improving generalization, and enabling models to maintain diverse hypotheses. Our early results demonstrate GFlowNet fine-tuning's potential for enhancing model performance in a search setting, which is especially relevant given the paradigm shift towards inference time compute scaling and "thinking slowly."