Graph topological property recovery with heat and wave dynamics-based features on graphs

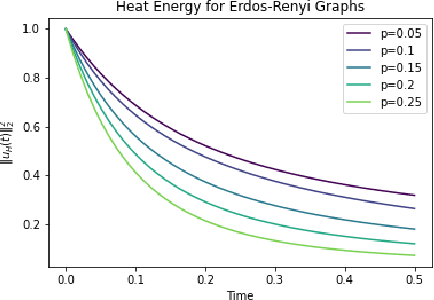
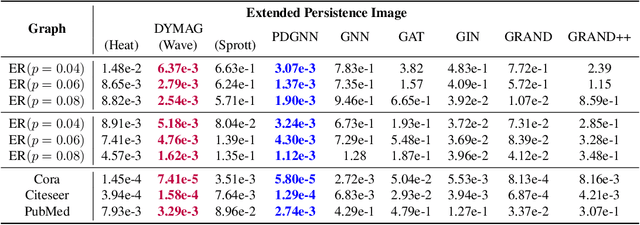
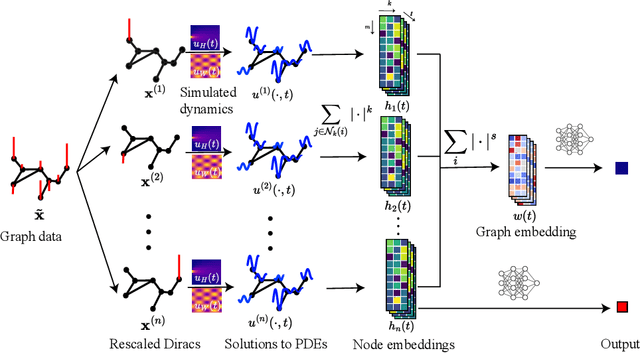
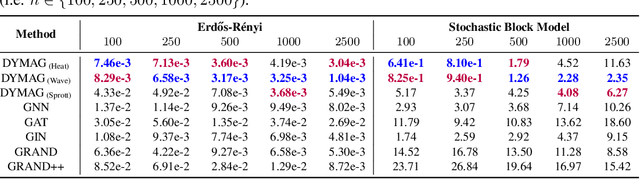
In this paper, we propose Graph Differential Equation Network (GDeNet), an approach that harnesses the expressive power of solutions to PDEs on a graph to obtain continuous node- and graph-level representations for various downstream tasks. We derive theoretical results connecting the dynamics of heat and wave equations to the spectral properties of the graph and to the behavior of continuous-time random walks on graphs. We demonstrate experimentally that these dynamics are able to capture salient aspects of graph geometry and topology by recovering generating parameters of random graphs, Ricci curvature, and persistent homology. Furthermore, we demonstrate the superior performance of GDeNet on real-world datasets including citation graphs, drug-like molecules, and proteins.