BrainDyn: A Sheaf Neural ODE for Generative Brain Dynamics

Efficient neural network models that generate brain-like dynamic activity can be a valuable resource for generating synthetic data, analyzing differences in brain transients under conditions such as testing perturbation activity or inferring the underlying generative dynamics. However, large language models (LLMs) or standard recurrent neural networks (RNNs) ignore the anatomical organization and therefore do not produce components that align with brain regions. On the other hand, graph-based networks often have very simple message passing rules that are not sufficiently expressive for brain-like dynamics. To address this, we introduce BrainDyn, a sheaf neural ordinary differential equation (neural ODE) model for continuous-time dynamics on structured brain graphs. BrainDyn encodes the recent activity history of each brain region using a long short-term memory (LSTM) model over a sliding temporal window to produce hidden states, or stalks, that are projected through learnable restriction maps into edge-specific shared spaces. Discrepancies between neighboring nodes in these shared spaces are characterized by a sheaf Laplacian that can facilitate message passing between neuronal units. The output of these messages is then fed to a neural ODE that governs the continuous-time evolution of neuronal activity. We evaluated BrainDyn on resting-state fMRI (PNC dataset), scalp EEG with focal epilepsy (TUSZ dataset), and simulated activity from the NEST spiking network simulator. BrainDyn achieves strong forecasting ability across modalities, and the resulting representations support downstream tasks including in silico perturbation prediction.

Can Computational Reducibility Lead to Transferable Models for Graph Combinatorial Optimization?

A key challenge in deriving unified neural solvers for combinatorial optimization (CO) is efficient generalization of models between a given set of tasks to new tasks not used during the initial training process. To address it, we first establish a new model, which uses a GCON module as a form of expressive message passing together with energy-based unsupervised loss functions. This model achieves high performance (often comparable with state-of-the-art results) across multiple CO tasks when trained individually on each task. We then leverage knowledge from the computational reducibility literature to propose pretraining and fine-tuning strategies that transfer effectively (a) between MVC, MIS and MaxClique, and (b) in a multi-task learning setting that additionally incorporates MaxCut, MDS and graph coloring. Additionally, in a leave-one-out, multi-task learning setting, we observe that pretraining on all but one task almost always leads to faster convergence on the remaining task when fine-tuning while avoiding negative transfer. Our findings indicate that learning common representations across multiple graph CO problems is viable through the use of expressive message passing coupled with pretraining strategies that are informed by the polynomial reduction literature, thereby taking an important step towards enabling the development of foundational models for neural CO. We provide an open-source implementation of our work at https://github.com/semihcanturk/COPT-MT .

InfoGain Wavelets: Furthering the Design of Diffusion Wavelets for Graph-Structured Data

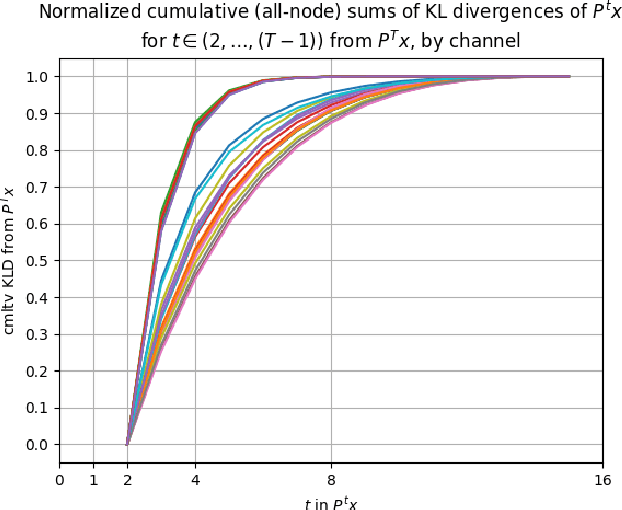
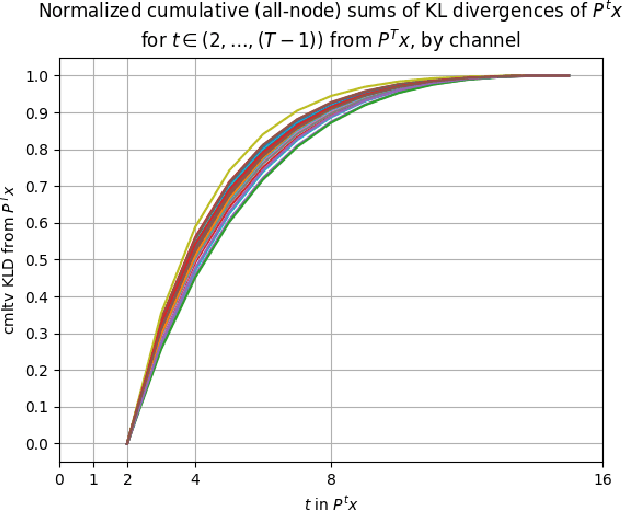
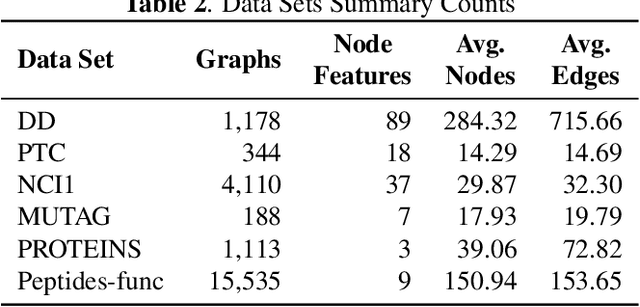
Diffusion wavelets extract information from graph signals at different scales of resolution by utilizing graph diffusion operators raised to various powers, known as diffusion scales. Traditionally, the diffusion scales are chosen to be dyadic integers, $\mathbf{2^j}$. Here, we propose a novel, unsupervised method for selecting the diffusion scales based on ideas from information theory. We then show that our method can be incorporated into wavelet-based GNNs via graph classification experiments.

HiPoNet: A Topology-Preserving Multi-View Neural Network For High Dimensional Point Cloud and Single-Cell Data

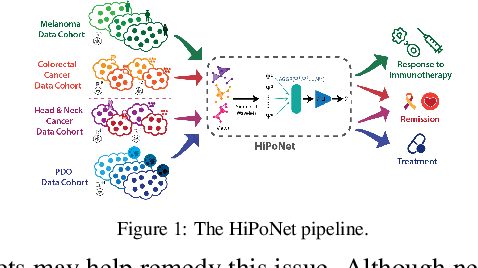
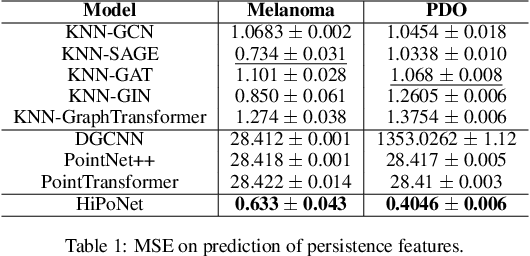
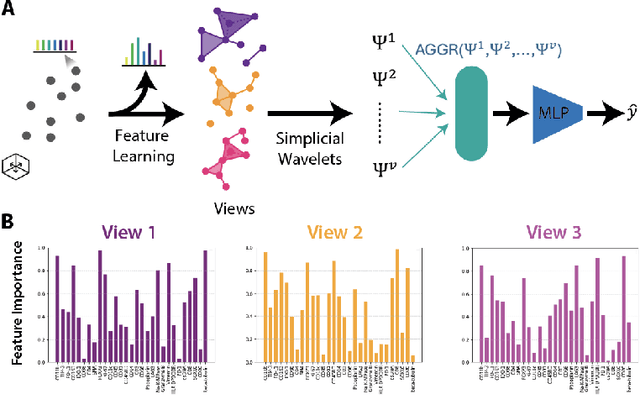
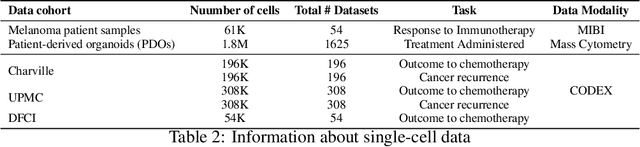
In this paper, we propose HiPoNet, an end-to-end differentiable neural network for regression, classification, and representation learning on high-dimensional point clouds. Single-cell data can have high dimensionality exceeding the capabilities of existing methods point cloud tailored for 3D data. Moreover, modern single-cell and spatial experiments now yield entire cohorts of datasets (i.e. one on every patient), necessitating models that can process large, high-dimensional point clouds at scale. Most current approaches build a single nearest-neighbor graph, discarding important geometric information. In contrast, HiPoNet forms higher-order simplicial complexes through learnable feature reweighting, generating multiple data views that disentangle distinct biological processes. It then employs simplicial wavelet transforms to extract multi-scale features - capturing both local and global topology. We empirically show that these components preserve topological information in the learned representations, and that HiPoNet significantly outperforms state-of-the-art point-cloud and graph-based models on single cell. We also show an application of HiPoNet on spatial transcriptomics datasets using spatial co-ordinates as one of the views. Overall, HiPoNet offers a robust and scalable solution for high-dimensional data analysis.

Convergence of Manifold Filter-Combine Networks

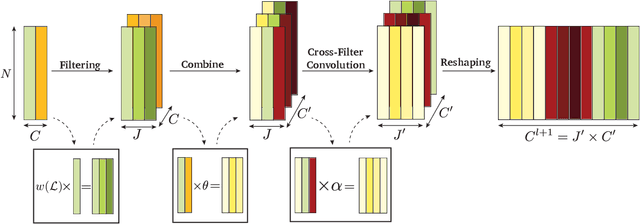
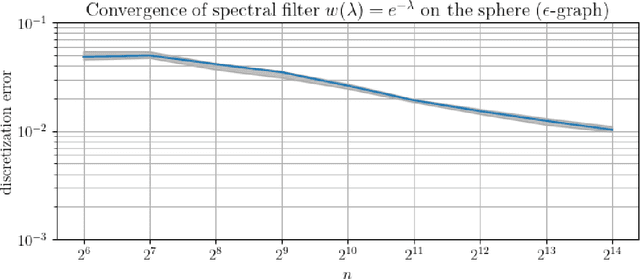
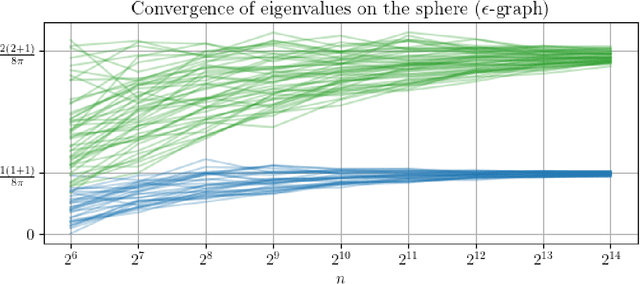
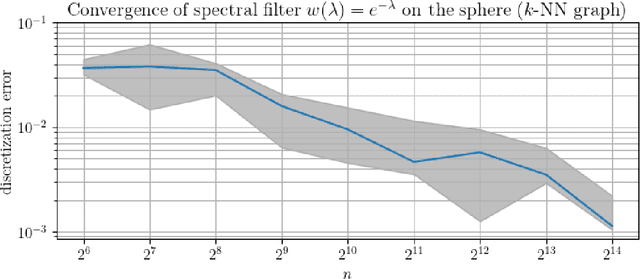
In order to better understand manifold neural networks (MNNs), we introduce Manifold Filter-Combine Networks (MFCNs). The filter-combine framework parallels the popular aggregate-combine paradigm for graph neural networks (GNNs) and naturally suggests many interesting families of MNNs which can be interpreted as the manifold analog of various popular GNNs. We then propose a method for implementing MFCNs on high-dimensional point clouds that relies on approximating the manifold by a sparse graph. We prove that our method is consistent in the sense that it converges to a continuum limit as the number of data points tends to infinity.

Hyperedge Representations with Hypergraph Wavelets: Applications to Spatial Transcriptomics

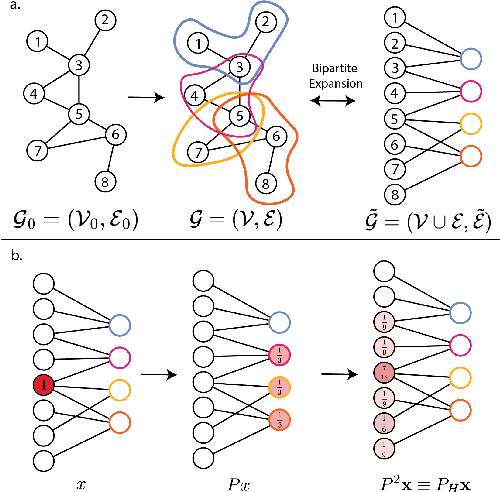
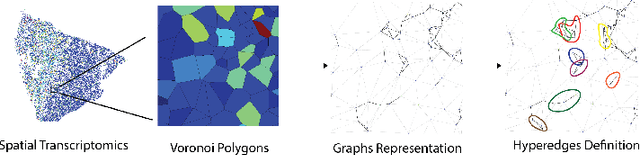
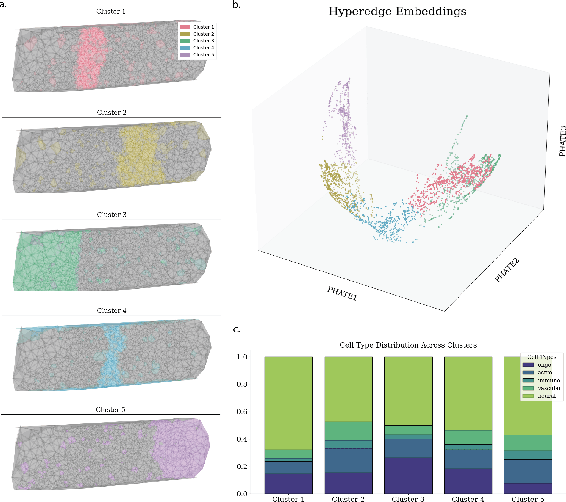
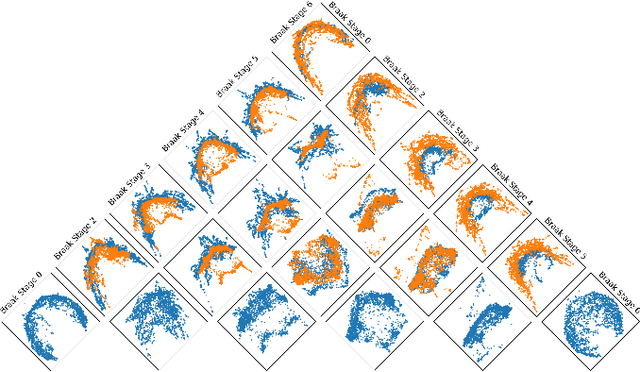
In many data-driven applications, higher-order relationships among multiple objects are essential in capturing complex interactions. Hypergraphs, which generalize graphs by allowing edges to connect any number of nodes, provide a flexible and powerful framework for modeling such higher-order relationships. In this work, we introduce hypergraph diffusion wavelets and describe their favorable spectral and spatial properties. We demonstrate their utility for biomedical discovery in spatially resolved transcriptomics by applying the method to represent disease-relevant cellular niches for Alzheimer's disease.

Towards a General GNN Framework for Combinatorial Optimization

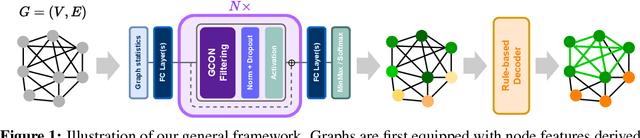
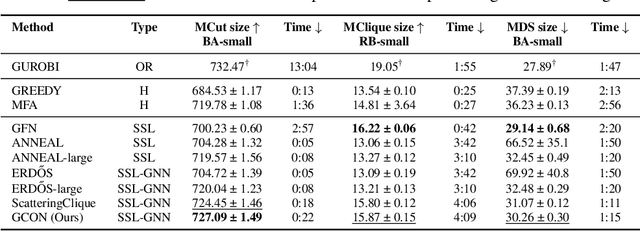
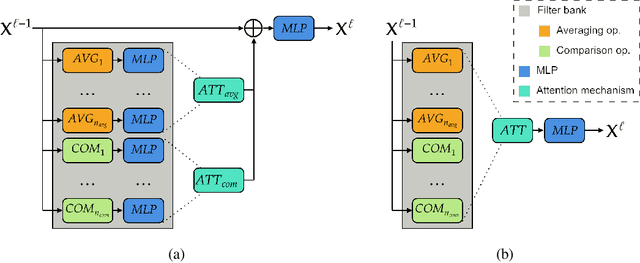
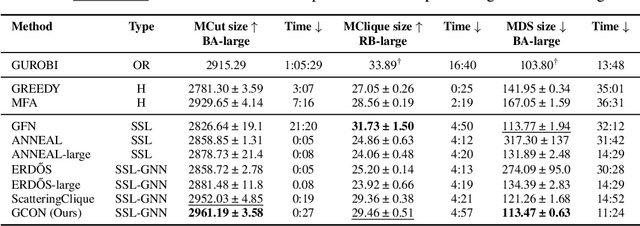
Graph neural networks (GNNs) have achieved great success for a variety of tasks such as node classification, graph classification, and link prediction. However, the use of GNNs (and machine learning more generally) to solve combinatorial optimization (CO) problems is much less explored. Here, we introduce a novel GNN architecture which leverages a complex filter bank and localized attention mechanisms designed to solve CO problems on graphs. We show how our method differentiates itself from prior GNN-based CO solvers and how it can be effectively applied to the maximum clique, minimum dominating set, and maximum cut problems in a self-supervised learning setting. In addition to demonstrating competitive overall performance across all tasks, we establish state-of-the-art results for the max cut problem.

Bayesian Formulations for Graph Spectral Denoising

We consider noisy signals which are defined on the vertices of a graph and present smoothing algorithms for the cases of Gaussian, dropout, and uniformly distributed noise. The signals are assumed to follow a prior distribution defined in the frequency domain which favors signals which are smooth across the edges of the graph. By pairing this prior distribution with our three models of noise generation, we propose \textit{Maximum A Posteriori} (M.A.P.) estimates of the true signal in the presence of noisy data and provide algorithms for computing the M.A.P. Finally, we demonstrate the algorithms' ability to effectively restore white noise on image data, and from severe dropout in toy \& EHR data.

BLIS-Net: Classifying and Analyzing Signals on Graphs

Graph neural networks (GNNs) have emerged as a powerful tool for tasks such as node classification and graph classification. However, much less work has been done on signal classification, where the data consists of many functions (referred to as signals) defined on the vertices of a single graph. These tasks require networks designed differently from those designed for traditional GNN tasks. Indeed, traditional GNNs rely on localized low-pass filters, and signals of interest may have intricate multi-frequency behavior and exhibit long range interactions. This motivates us to introduce the BLIS-Net (Bi-Lipschitz Scattering Net), a novel GNN that builds on the previously introduced geometric scattering transform. Our network is able to capture both local and global signal structure and is able to capture both low-frequency and high-frequency information. We make several crucial changes to the original geometric scattering architecture which we prove increase the ability of our network to capture information about the input signal and show that BLIS-Net achieves superior performance on both synthetic and real-world data sets based on traffic flow and fMRI data.

Graph topological property recovery with heat and wave dynamics-based features on graphs

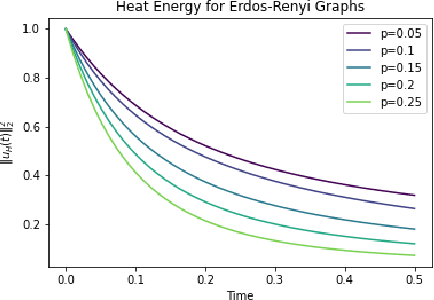
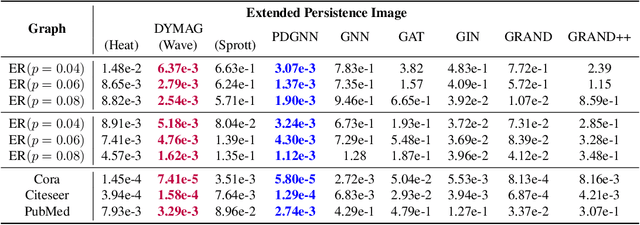
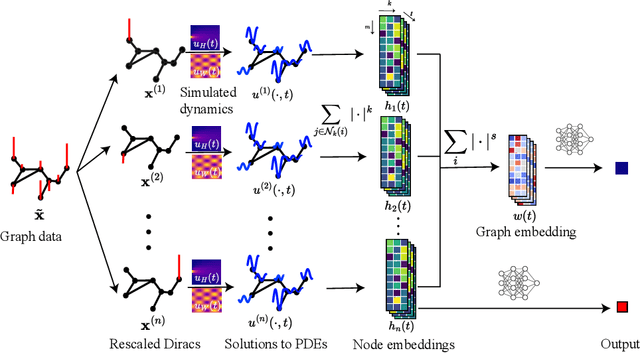
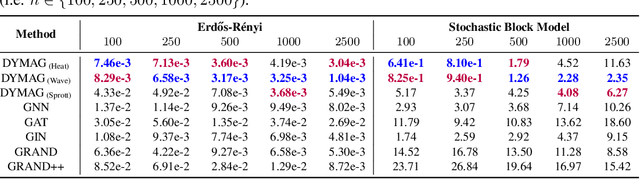
In this paper, we propose Graph Differential Equation Network (GDeNet), an approach that harnesses the expressive power of solutions to PDEs on a graph to obtain continuous node- and graph-level representations for various downstream tasks. We derive theoretical results connecting the dynamics of heat and wave equations to the spectral properties of the graph and to the behavior of continuous-time random walks on graphs. We demonstrate experimentally that these dynamics are able to capture salient aspects of graph geometry and topology by recovering generating parameters of random graphs, Ricci curvature, and persistent homology. Furthermore, we demonstrate the superior performance of GDeNet on real-world datasets including citation graphs, drug-like molecules, and proteins.