Hyperedge Representations with Hypergraph Wavelets: Applications to Spatial Transcriptomics

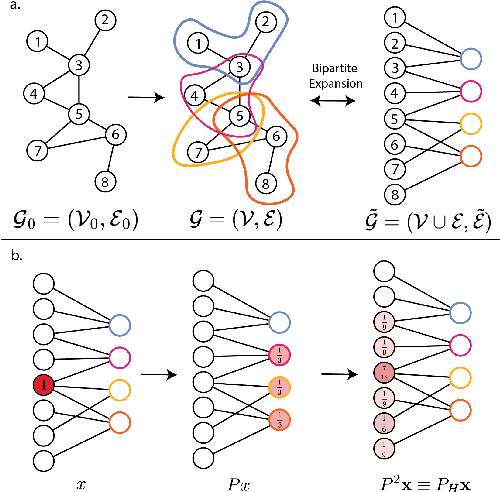
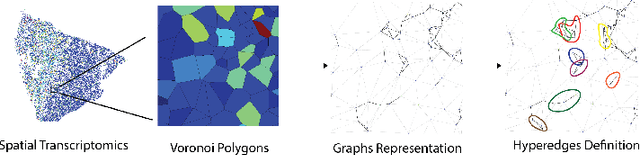
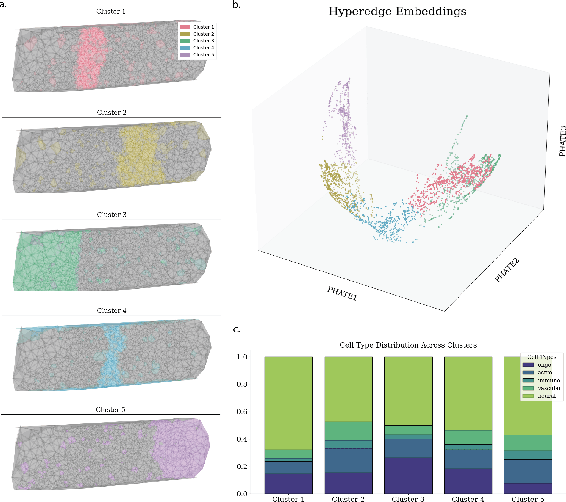
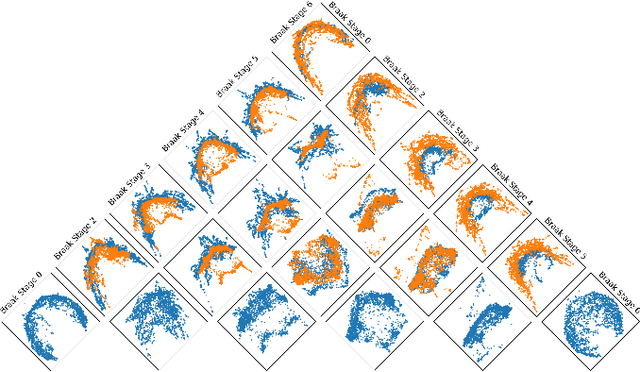
In many data-driven applications, higher-order relationships among multiple objects are essential in capturing complex interactions. Hypergraphs, which generalize graphs by allowing edges to connect any number of nodes, provide a flexible and powerful framework for modeling such higher-order relationships. In this work, we introduce hypergraph diffusion wavelets and describe their favorable spectral and spatial properties. We demonstrate their utility for biomedical discovery in spatially resolved transcriptomics by applying the method to represent disease-relevant cellular niches for Alzheimer's disease.