Smita Krishnaswamy
Yale University
Self-Supervised Visual Prompting for Cross-Domain Road Damage Detection
Nov 16, 2025
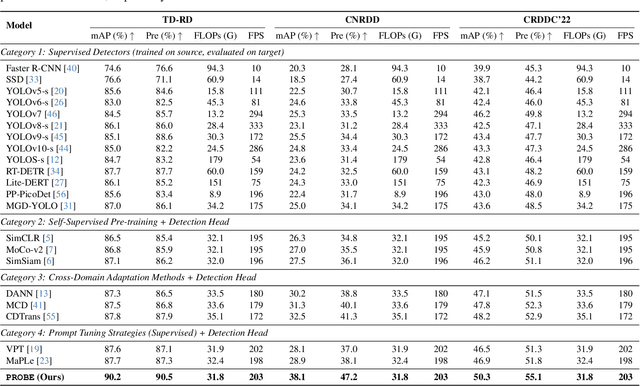
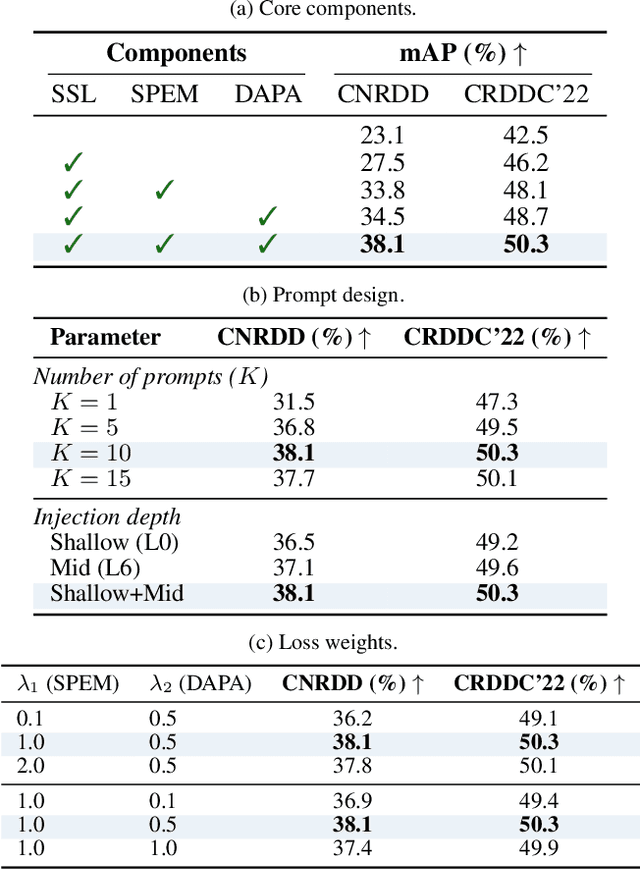

Abstract:The deployment of automated pavement defect detection is often hindered by poor cross-domain generalization. Supervised detectors achieve strong in-domain accuracy but require costly re-annotation for new environments, while standard self-supervised methods capture generic features and remain vulnerable to domain shift. We propose \ours, a self-supervised framework that \emph{visually probes} target domains without labels. \ours introduces a Self-supervised Prompt Enhancement Module (SPEM), which derives defect-aware prompts from unlabeled target data to guide a frozen ViT backbone, and a Domain-Aware Prompt Alignment (DAPA) objective, which aligns prompt-conditioned source and target representations. Experiments on four challenging benchmarks show that \ours consistently outperforms strong supervised, self-supervised, and adaptation baselines, achieving robust zero-shot transfer, improved resilience to domain variations, and high data efficiency in few-shot adaptation. These results highlight self-supervised prompting as a practical direction for building scalable and adaptive visual inspection systems. Source code is publicly available: https://github.com/xixiaouab/PROBE/tree/main
STAGED: A Multi-Agent Neural Network for Learning Cellular Interaction Dynamics
Jul 15, 2025Abstract:The advent of single-cell technology has significantly improved our understanding of cellular states and subpopulations in various tissues under normal and diseased conditions by employing data-driven approaches such as clustering and trajectory inference. However, these methods consider cells as independent data points of population distributions. With spatial transcriptomics, we can represent cellular organization, along with dynamic cell-cell interactions that lead to changes in cell state. Still, key computational advances are necessary to enable the data-driven learning of such complex interactive cellular dynamics. While agent-based modeling (ABM) provides a powerful framework, traditional approaches rely on handcrafted rules derived from domain knowledge rather than data-driven approaches. To address this, we introduce Spatio Temporal Agent-Based Graph Evolution Dynamics(STAGED) integrating ABM with deep learning to model intercellular communication, and its effect on the intracellular gene regulatory network. Using graph ODE networks (GDEs) with shared weights per cell type, our approach represents genes as vertices and interactions as directed edges, dynamically learning their strengths through a designed attention mechanism. Trained to match continuous trajectories of simulated as well as inferred trajectories from spatial transcriptomics data, the model captures both intercellular and intracellular interactions, enabling a more adaptive and accurate representation of cellular dynamics.
HEIST: A Graph Foundation Model for Spatial Transcriptomics and Proteomics Data
Jun 11, 2025Abstract:Single-cell transcriptomics has become a great source for data-driven insights into biology, enabling the use of advanced deep learning methods to understand cellular heterogeneity and transcriptional regulation at the single-cell level. With the advent of spatial transcriptomics data we have the promise of learning about cells within a tissue context as it provides both spatial coordinates and transcriptomic readouts. However, existing models either ignore spatial resolution or the gene regulatory information. Gene regulation in cells can change depending on microenvironmental cues from neighboring cells, but existing models neglect gene regulatory patterns with hierarchical dependencies across levels of abstraction. In order to create contextualized representations of cells and genes from spatial transcriptomics data, we introduce HEIST, a hierarchical graph transformer-based foundation model for spatial transcriptomics and proteomics data. HEIST models tissue as spatial cellular neighborhood graphs, and each cell is, in turn, modeled as a gene regulatory network graph. The framework includes a hierarchical graph transformer that performs cross-level message passing and message passing within levels. HEIST is pre-trained on 22.3M cells from 124 tissues across 15 organs using spatially-aware contrastive learning and masked auto-encoding objectives. Unsupervised analysis of HEIST representations of cells, shows that it effectively encodes the microenvironmental influences in cell embeddings, enabling the discovery of spatially-informed subpopulations that prior models fail to differentiate. Further, HEIST achieves state-of-the-art results on four downstream task such as clinical outcome prediction, cell type annotation, gene imputation, and spatially-informed cell clustering across multiple technologies, highlighting the importance of hierarchical modeling and GRN-based representations.
HELM: Hyperbolic Large Language Models via Mixture-of-Curvature Experts
May 30, 2025



Abstract:Large language models (LLMs) have shown great success in text modeling tasks across domains. However, natural language exhibits inherent semantic hierarchies and nuanced geometric structure, which current LLMs do not capture completely owing to their reliance on Euclidean operations. Recent studies have also shown that not respecting the geometry of token embeddings leads to training instabilities and degradation of generative capabilities. These findings suggest that shifting to non-Euclidean geometries can better align language models with the underlying geometry of text. We thus propose to operate fully in Hyperbolic space, known for its expansive, scale-free, and low-distortion properties. We thus introduce HELM, a family of HypErbolic Large Language Models, offering a geometric rethinking of the Transformer-based LLM that addresses the representational inflexibility, missing set of necessary operations, and poor scalability of existing hyperbolic LMs. We additionally introduce a Mixture-of-Curvature Experts model, HELM-MICE, where each expert operates in a distinct curvature space to encode more fine-grained geometric structure from text, as well as a dense model, HELM-D. For HELM-MICE, we further develop hyperbolic Multi-Head Latent Attention (HMLA) for efficient, reduced-KV-cache training and inference. For both models, we develop essential hyperbolic equivalents of rotary positional encodings and RMS normalization. We are the first to train fully hyperbolic LLMs at billion-parameter scale, and evaluate them on well-known benchmarks such as MMLU and ARC, spanning STEM problem-solving, general knowledge, and commonsense reasoning. Our results show consistent gains from our HELM architectures -- up to 4% -- over popular Euclidean architectures used in LLaMA and DeepSeek, highlighting the efficacy and enhanced reasoning afforded by hyperbolic geometry in large-scale LM pretraining.
InfoGain Wavelets: Furthering the Design of Diffusion Wavelets for Graph-Structured Data
Apr 08, 2025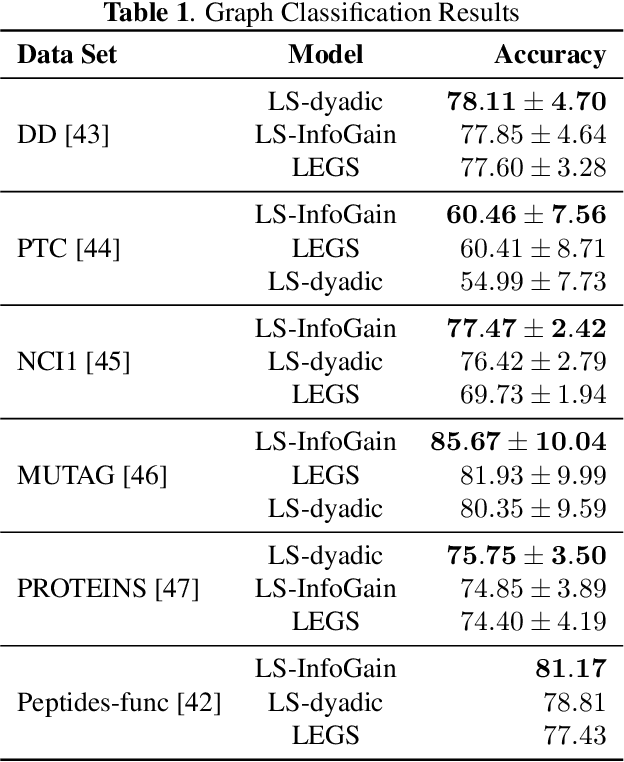
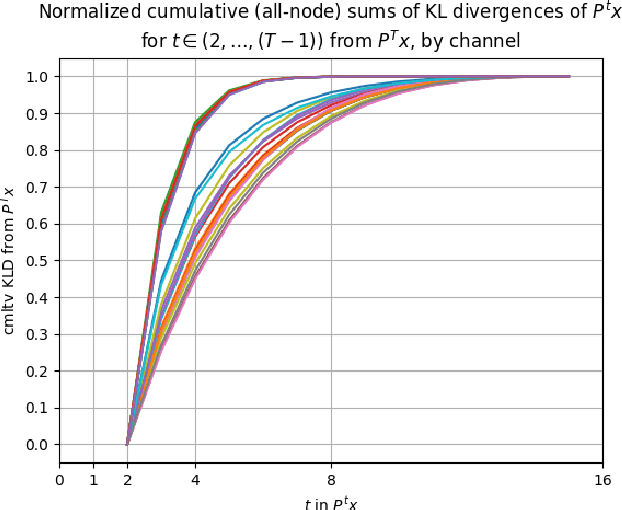
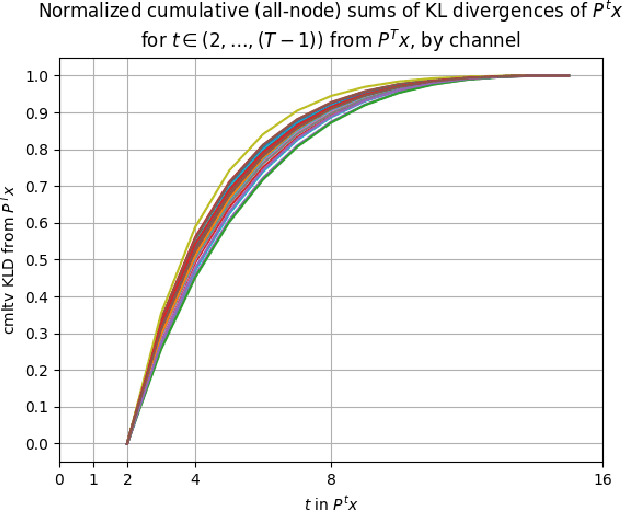
Abstract:Diffusion wavelets extract information from graph signals at different scales of resolution by utilizing graph diffusion operators raised to various powers, known as diffusion scales. Traditionally, the diffusion scales are chosen to be dyadic integers, $\mathbf{2^j}$. Here, we propose a novel, unsupervised method for selecting the diffusion scales based on ideas from information theory. We then show that our method can be incorporated into wavelet-based GNNs via graph classification experiments.
HiPoNet: A Topology-Preserving Multi-View Neural Network For High Dimensional Point Cloud and Single-Cell Data
Feb 11, 2025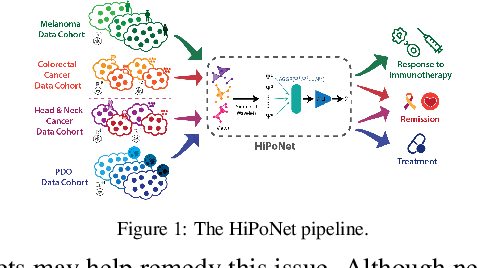
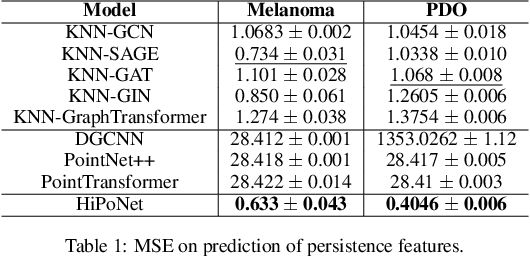
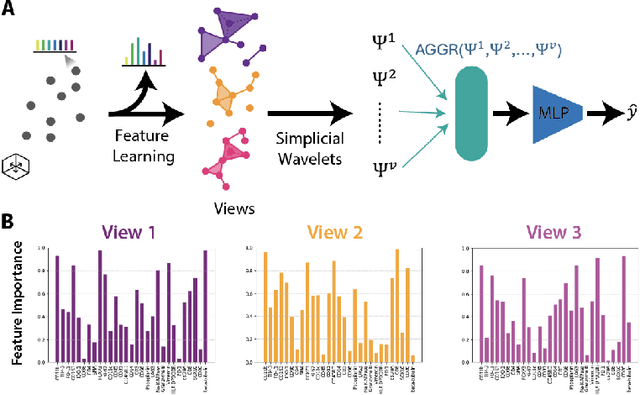
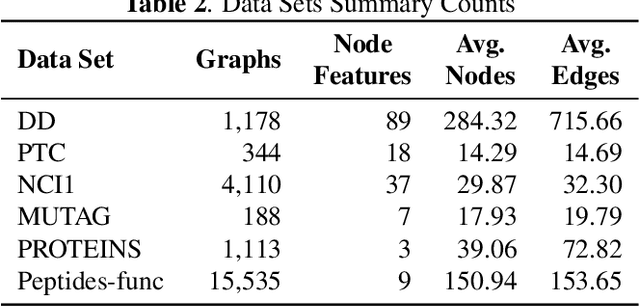
Abstract:In this paper, we propose HiPoNet, an end-to-end differentiable neural network for regression, classification, and representation learning on high-dimensional point clouds. Single-cell data can have high dimensionality exceeding the capabilities of existing methods point cloud tailored for 3D data. Moreover, modern single-cell and spatial experiments now yield entire cohorts of datasets (i.e. one on every patient), necessitating models that can process large, high-dimensional point clouds at scale. Most current approaches build a single nearest-neighbor graph, discarding important geometric information. In contrast, HiPoNet forms higher-order simplicial complexes through learnable feature reweighting, generating multiple data views that disentangle distinct biological processes. It then employs simplicial wavelet transforms to extract multi-scale features - capturing both local and global topology. We empirically show that these components preserve topological information in the learned representations, and that HiPoNet significantly outperforms state-of-the-art point-cloud and graph-based models on single cell. We also show an application of HiPoNet on spatial transcriptomics datasets using spatial co-ordinates as one of the views. Overall, HiPoNet offers a robust and scalable solution for high-dimensional data analysis.
Principal Curvatures Estimation with Applications to Single Cell Data
Feb 06, 2025



Abstract:The rapidly growing field of single-cell transcriptomic sequencing (scRNAseq) presents challenges for data analysis due to its massive datasets. A common method in manifold learning consists in hypothesizing that datasets lie on a lower dimensional manifold. This allows to study the geometry of point clouds by extracting meaningful descriptors like curvature. In this work, we will present Adaptive Local PCA (AdaL-PCA), a data-driven method for accurately estimating various notions of intrinsic curvature on data manifolds, in particular principal curvatures for surfaces. The model relies on local PCA to estimate the tangent spaces. The evaluation of AdaL-PCA on sampled surfaces shows state-of-the-art results. Combined with a PHATE embedding, the model applied to single-cell RNA sequencing data allows us to identify key variations in the cellular differentiation.
Exploring the Manifold of Neural Networks Using Diffusion Geometry
Nov 19, 2024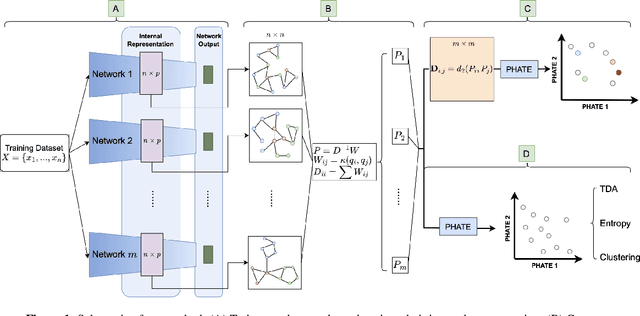

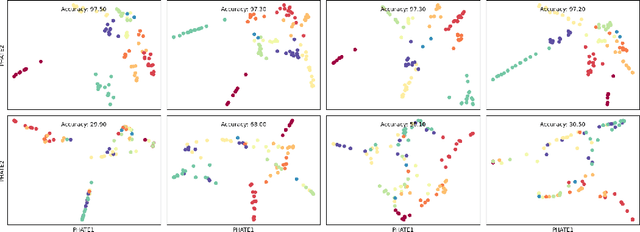
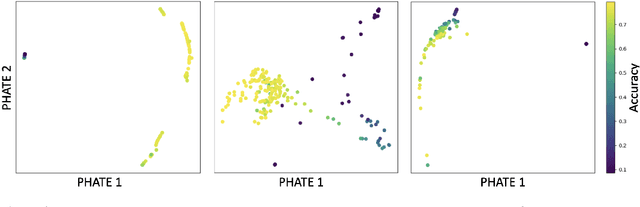
Abstract:Drawing motivation from the manifold hypothesis, which posits that most high-dimensional data lies on or near low-dimensional manifolds, we apply manifold learning to the space of neural networks. We learn manifolds where datapoints are neural networks by introducing a distance between the hidden layer representations of the neural networks. These distances are then fed to the non-linear dimensionality reduction algorithm PHATE to create a manifold of neural networks. We characterize this manifold using features of the representation, including class separation, hierarchical cluster structure, spectral entropy, and topological structure. Our analysis reveals that high-performing networks cluster together in the manifold, displaying consistent embedding patterns across all these features. Finally, we demonstrate the utility of this approach for guiding hyperparameter optimization and neural architecture search by sampling from the manifold.
ProtSCAPE: Mapping the landscape of protein conformations in molecular dynamics
Oct 27, 2024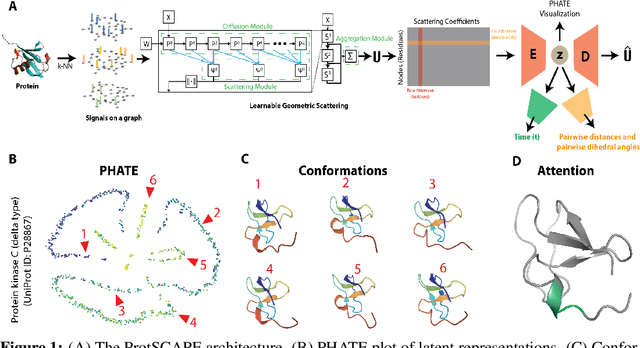
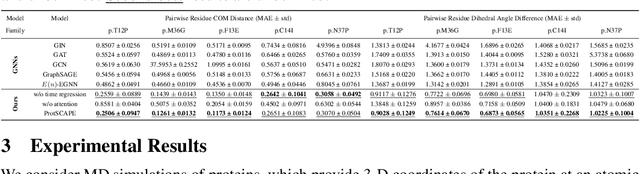
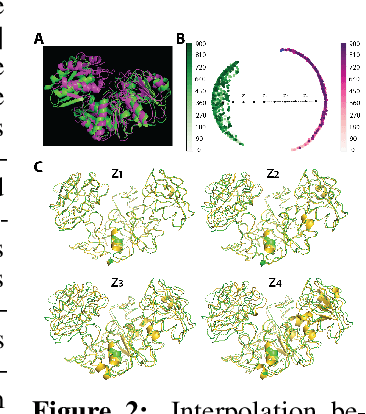
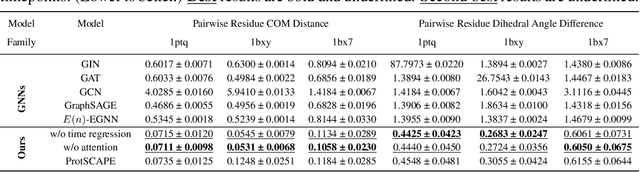
Abstract:Understanding the dynamic nature of protein structures is essential for comprehending their biological functions. While significant progress has been made in predicting static folded structures, modeling protein motions on microsecond to millisecond scales remains challenging. To address these challenges, we introduce a novel deep learning architecture, Protein Transformer with Scattering, Attention, and Positional Embedding (ProtSCAPE), which leverages the geometric scattering transform alongside transformer-based attention mechanisms to capture protein dynamics from molecular dynamics (MD) simulations. ProtSCAPE utilizes the multi-scale nature of the geometric scattering transform to extract features from protein structures conceptualized as graphs and integrates these features with dual attention structures that focus on residues and amino acid signals, generating latent representations of protein trajectories. Furthermore, ProtSCAPE incorporates a regression head to enforce temporally coherent latent representations.
Convergence of Manifold Filter-Combine Networks
Oct 18, 2024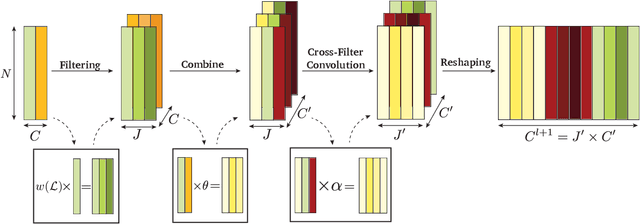
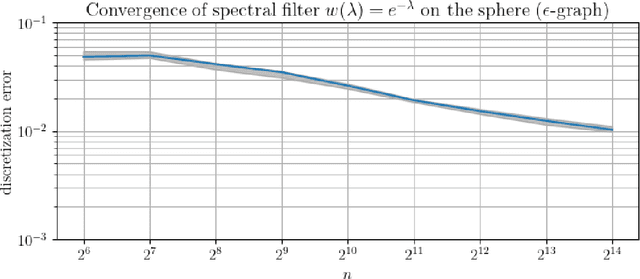
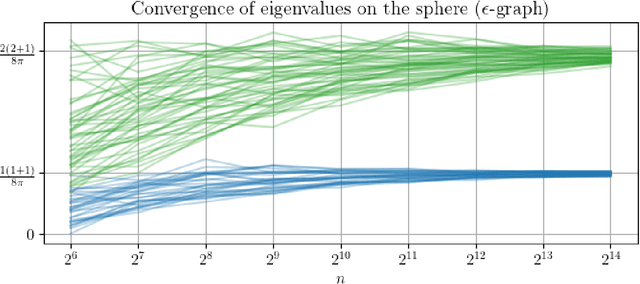
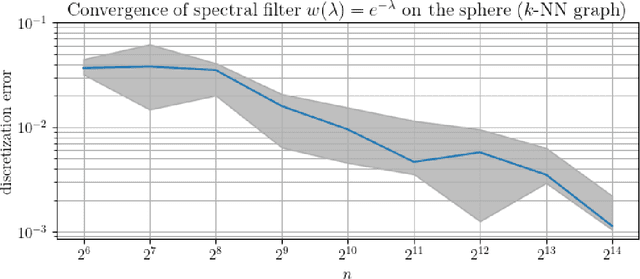
Abstract:In order to better understand manifold neural networks (MNNs), we introduce Manifold Filter-Combine Networks (MFCNs). The filter-combine framework parallels the popular aggregate-combine paradigm for graph neural networks (GNNs) and naturally suggests many interesting families of MNNs which can be interpreted as the manifold analog of various popular GNNs. We then propose a method for implementing MFCNs on high-dimensional point clouds that relies on approximating the manifold by a sparse graph. We prove that our method is consistent in the sense that it converges to a continuum limit as the number of data points tends to infinity.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge