Principal Curvatures Estimation with Applications to Single Cell Data

The rapidly growing field of single-cell transcriptomic sequencing (scRNAseq) presents challenges for data analysis due to its massive datasets. A common method in manifold learning consists in hypothesizing that datasets lie on a lower dimensional manifold. This allows to study the geometry of point clouds by extracting meaningful descriptors like curvature. In this work, we will present Adaptive Local PCA (AdaL-PCA), a data-driven method for accurately estimating various notions of intrinsic curvature on data manifolds, in particular principal curvatures for surfaces. The model relies on local PCA to estimate the tangent spaces. The evaluation of AdaL-PCA on sampled surfaces shows state-of-the-art results. Combined with a PHATE embedding, the model applied to single-cell RNA sequencing data allows us to identify key variations in the cellular differentiation.

Learnable Filters for Geometric Scattering Modules

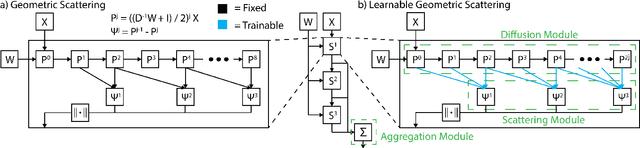
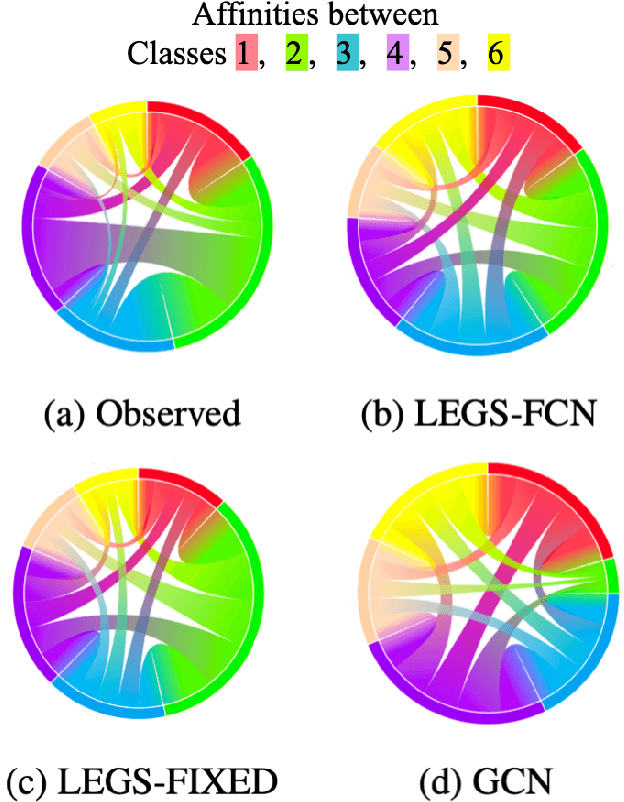
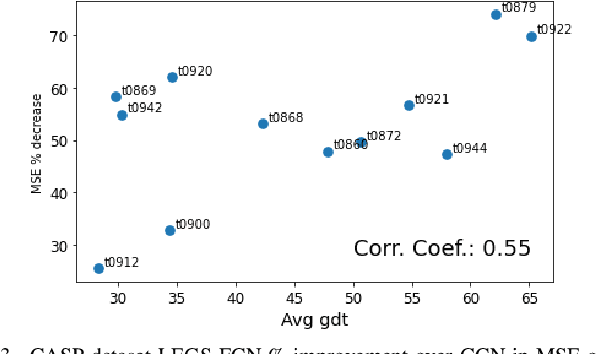
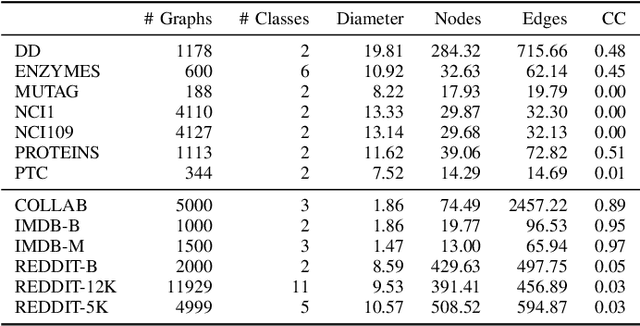
We propose a new graph neural network (GNN) module, based on relaxations of recently proposed geometric scattering transforms, which consist of a cascade of graph wavelet filters. Our learnable geometric scattering (LEGS) module enables adaptive tuning of the wavelets to encourage band-pass features to emerge in learned representations. The incorporation of our LEGS-module in GNNs enables the learning of longer-range graph relations compared to many popular GNNs, which often rely on encoding graph structure via smoothness or similarity between neighbors. Further, its wavelet priors result in simplified architectures with significantly fewer learned parameters compared to competing GNNs. We demonstrate the predictive performance of LEGS-based networks on graph classification benchmarks, as well as the descriptive quality of their learned features in biochemical graph data exploration tasks. Our results show that LEGS-based networks match or outperforms popular GNNs, as well as the original geometric scattering construction, on many datasets, in particular in biochemical domains, while retaining certain mathematical properties of handcrafted (non-learned) geometric scattering.