Principal Curvatures Estimation with Applications to Single Cell Data

The rapidly growing field of single-cell transcriptomic sequencing (scRNAseq) presents challenges for data analysis due to its massive datasets. A common method in manifold learning consists in hypothesizing that datasets lie on a lower dimensional manifold. This allows to study the geometry of point clouds by extracting meaningful descriptors like curvature. In this work, we will present Adaptive Local PCA (AdaL-PCA), a data-driven method for accurately estimating various notions of intrinsic curvature on data manifolds, in particular principal curvatures for surfaces. The model relies on local PCA to estimate the tangent spaces. The evaluation of AdaL-PCA on sampled surfaces shows state-of-the-art results. Combined with a PHATE embedding, the model applied to single-cell RNA sequencing data allows us to identify key variations in the cellular differentiation.

No Metric to Rule Them All: Toward Principled Evaluations of Graph-Learning Datasets

Benchmark datasets have proved pivotal to the success of graph learning, and good benchmark datasets are crucial to guide the development of the field. Recent research has highlighted problems with graph-learning datasets and benchmarking practices -- revealing, for example, that methods which ignore the graph structure can outperform graph-based approaches on popular benchmark datasets. Such findings raise two questions: (1) What makes a good graph-learning dataset, and (2) how can we evaluate dataset quality in graph learning? Our work addresses these questions. As the classic evaluation setup uses datasets to evaluate models, it does not apply to dataset evaluation. Hence, we start from first principles. Observing that graph-learning datasets uniquely combine two modes -- the graph structure and the node features -- , we introduce RINGS, a flexible and extensible mode-perturbation framework to assess the quality of graph-learning datasets based on dataset ablations -- i.e., by quantifying differences between the original dataset and its perturbed representations. Within this framework, we propose two measures -- performance separability and mode complementarity -- as evaluation tools, each assessing, from a distinct angle, the capacity of a graph dataset to benchmark the power and efficacy of graph-learning methods. We demonstrate the utility of our framework for graph-learning dataset evaluation in an extensive set of experiments and derive actionable recommendations for improving the evaluation of graph-learning methods. Our work opens new research directions in data-centric graph learning, and it constitutes a first step toward the systematic evaluation of evaluations.

Topology meets Machine Learning: An Introduction using the Euler Characteristic Transform

This overview article makes the case for how topological concepts can enrich research in machine learning. Using the Euler Characteristic Transform (ECT), a geometrical-topological invariant, as a running example, I present different use cases that result in more efficient models for analyzing point clouds, graphs, and meshes. Moreover, I outline a vision for how topological concepts could be used in the future, comprising (1) the learning of functions on topological spaces, (2) the building of hybrid models that imbue neural networks with knowledge about the topological information in data, and (3) the analysis of qualitative properties of neural networks. With current research already addressing some of these aspects, this article thus serves as an introduction and invitation to this nascent area of research.

Detecting and Approximating Redundant Computational Blocks in Neural Networks

Deep neural networks often learn similar internal representations, both across different models and within their own layers. While inter-network similarities have enabled techniques such as model stitching and merging, intra-network similarities present new opportunities for designing more efficient architectures. In this paper, we investigate the emergence of these internal similarities across different layers in diverse neural architectures, showing that similarity patterns emerge independently of the datataset used. We introduce a simple metric, Block Redundancy, to detect redundant blocks, providing a foundation for future architectural optimization methods. Building on this, we propose Redundant Blocks Approximation (RBA), a general framework that identifies and approximates one or more redundant computational blocks using simpler transformations. We show that the transformation $\mathcal{T}$ between two representations can be efficiently computed in closed-form, and it is enough to replace the redundant blocks from the network. RBA reduces model parameters and time complexity while maintaining good performance. We validate our method on classification tasks in the vision domain using a variety of pretrained foundational models and datasets.

Diss-l-ECT: Dissecting Graph Data with local Euler Characteristic Transforms

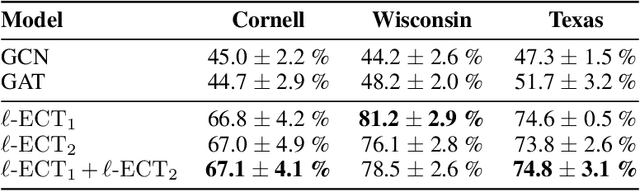
The Euler Characteristic Transform (ECT) is an efficiently-computable geometrical-topological invariant that characterizes the global shape of data. In this paper, we introduce the Local Euler Characteristic Transform ($\ell$-ECT), a novel extension of the ECT particularly designed to enhance expressivity and interpretability in graph representation learning. Unlike traditional Graph Neural Networks (GNNs), which may lose critical local details through aggregation, the $\ell$-ECT provides a lossless representation of local neighborhoods. This approach addresses key limitations in GNNs by preserving nuanced local structures while maintaining global interpretability. Moreover, we construct a rotation-invariant metric based on $\ell$-ECTs for spatial alignment of data spaces. Our method exhibits superior performance than standard GNNs on a variety of node classification tasks, particularly in graphs with high heterophily.

MANTRA: The Manifold Triangulations Assemblage

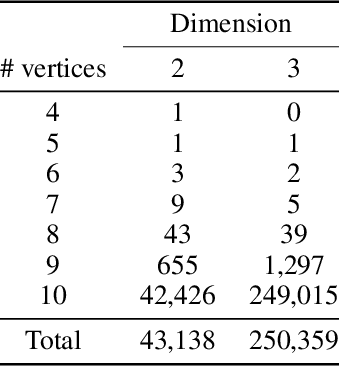
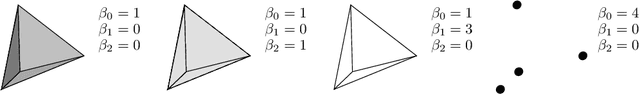
The rising interest in leveraging higher-order interactions present in complex systems has led to a surge in more expressive models exploiting high-order structures in the data, especially in topological deep learning (TDL), which designs neural networks on high-order domains such as simplicial complexes. However, progress in this field is hindered by the scarcity of datasets for benchmarking these architectures. To address this gap, we introduce MANTRA, the first large-scale, diverse, and intrinsically high order dataset for benchmarking high-order models, comprising over 43,000 and 249,000 triangulations of surfaces and three-dimensional manifolds, respectively. With MANTRA, we assess several graph- and simplicial complex-based models on three topological classification tasks. We demonstrate that while simplicial complex-based neural networks generally outperform their graph-based counterparts in capturing simple topological invariants, they also struggle, suggesting a rethink of TDL. Thus, MANTRA serves as a benchmark for assessing and advancing topological methods, leading the way for more effective high-order models.

CliquePH: Higher-Order Information for Graph Neural Networks through Persistent Homology on Clique Graphs

Graph neural networks have become the default choice by practitioners for graph learning tasks such as graph classification and node classification. Nevertheless, popular graph neural network models still struggle to capture higher-order information, i.e., information that goes \emph{beyond} pairwise interactions. Recent work has shown that persistent homology, a tool from topological data analysis, can enrich graph neural networks with topological information that they otherwise could not capture. Calculating such features is efficient for dimension 0 (connected components) and dimension 1 (cycles). However, when it comes to higher-order structures, it does not scale well, with a complexity of $O(n^d)$, where $n$ is the number of nodes and $d$ is the order of the structures. In this work, we introduce a novel method that extracts information about higher-order structures in the graph while still using the efficient low-dimensional persistent homology algorithm. On standard benchmark datasets, we show that our method can lead to up to $31\%$ improvements in test accuracy.

Characterizing Physician Referral Networks with Ricci Curvature

Identifying (a) systemic barriers to quality healthcare access and (b) key indicators of care efficacy in the United States remains a significant challenge. To improve our understanding of regional disparities in care delivery, we introduce a novel application of curvature, a geometrical-topological property of networks, to Physician Referral Networks. Our initial findings reveal that Forman-Ricci and Ollivier-Ricci curvature measures, which are known for their expressive power in characterizing network structure, offer promising indicators for detecting variations in healthcare efficacy while capturing a range of significant regional demographic features. We also present APPARENT, an open-source tool that leverages Ricci curvature and other network features to examine correlations between regional Physician Referral Networks structure, local census data, healthcare effectiveness, and patient outcomes.

Persistent Homology via Ellipsoids

Persistent homology is one of the most popular methods in Topological Data Analysis. An initial step in any analysis with persistent homology involves constructing a nested sequence of simplicial complexes, called a filtration, from a point cloud. There is an abundance of different complexes to choose from, with Rips, Alpha, and witness complexes being popular choices. In this manuscript, we build a different type of a geometrically-informed simplicial complex, called an ellipsoid complex. This complex is based on the idea that ellipsoids aligned with tangent directions better approximate the data compared to conventional (Euclidean) balls centered at sample points that are used in the construction of Rips and Alpha complexes, for instance. We use Principal Component Analysis to estimate tangent spaces directly from samples and present algorithms as well as an implementation for computing ellipsoid barcodes, i.e., topological descriptors based on ellipsoid complexes. Furthermore, we conduct extensive experiments and compare ellipsoid barcodes with standard Rips barcodes. Our findings indicate that ellipsoid complexes are particularly effective for estimating homology of manifolds and spaces with bottlenecks from samples. In particular, the persistence intervals corresponding to a ground-truth topological feature are longer compared to the intervals obtained when using the Rips complex of the data. Furthermore, ellipsoid barcodes lead to better classification results in sparsely-sampled point clouds. Finally, we demonstrate that ellipsoid barcodes outperform Rips barcodes in classification tasks.

Position Paper: Challenges and Opportunities in Topological Deep Learning

Topological deep learning (TDL) is a rapidly evolving field that uses topological features to understand and design deep learning models. This paper posits that TDL may complement graph representation learning and geometric deep learning by incorporating topological concepts, and can thus provide a natural choice for various machine learning settings. To this end, this paper discusses open problems in TDL, ranging from practical benefits to theoretical foundations. For each problem, it outlines potential solutions and future research opportunities. At the same time, this paper serves as an invitation to the scientific community to actively participate in TDL research to unlock the potential of this emerging field.