Diss-l-ECT: Dissecting Graph Data with local Euler Characteristic Transforms

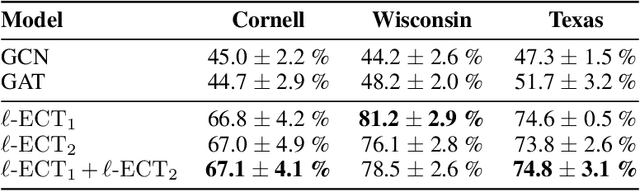
The Euler Characteristic Transform (ECT) is an efficiently-computable geometrical-topological invariant that characterizes the global shape of data. In this paper, we introduce the Local Euler Characteristic Transform ($\ell$-ECT), a novel extension of the ECT particularly designed to enhance expressivity and interpretability in graph representation learning. Unlike traditional Graph Neural Networks (GNNs), which may lose critical local details through aggregation, the $\ell$-ECT provides a lossless representation of local neighborhoods. This approach addresses key limitations in GNNs by preserving nuanced local structures while maintaining global interpretability. Moreover, we construct a rotation-invariant metric based on $\ell$-ECTs for spatial alignment of data spaces. Our method exhibits superior performance than standard GNNs on a variety of node classification tasks, particularly in graphs with high heterophily.

TOAST: Topological Algorithm for Singularity Tracking

The manifold hypothesis, which assumes that data lie on or close to an unknown manifold of low intrinsic dimensionality, is a staple of modern machine learning research. However, recent work has shown that real-world data exhibit distinct non-manifold structures, which result in singularities that can lead to erroneous conclusions about the data. Detecting such singularities is therefore crucial as a precursor to interpolation and inference tasks. We address detecting singularities by developing (i) persistent local homology, a new topology-driven framework for quantifying the intrinsic dimension of a data set locally, and (ii) Euclidicity, a topology-based multi-scale measure for assessing the 'manifoldness' of individual points. We show that our approach can reliably identify singularities of complex spaces, while also capturing singular structures in real-world data sets.