Towards a Foundation Model for Communication Systems

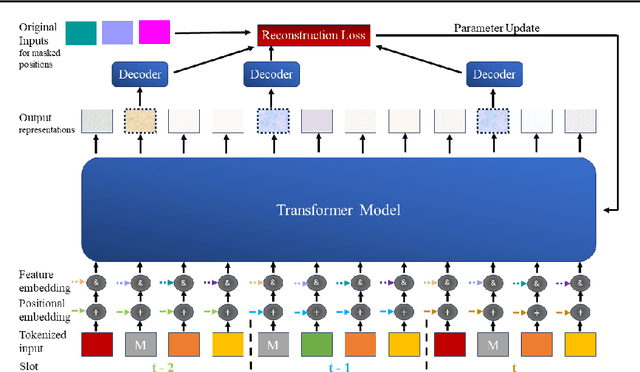
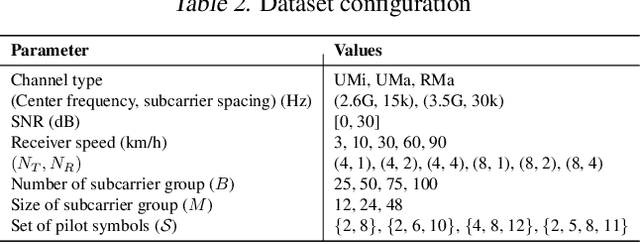
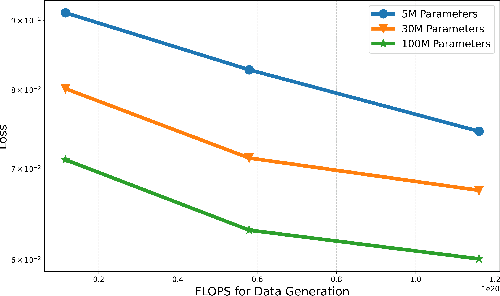
Artificial Intelligence (AI) has demonstrated unprecedented performance across various domains, and its application to communication systems is an active area of research. While current methods focus on task-specific solutions, the broader trend in AI is shifting toward large general models capable of supporting multiple applications. In this work, we take a step toward a foundation model for communication data--a transformer-based, multi-modal model designed to operate directly on communication data. We propose methodologies to address key challenges, including tokenization, positional embedding, multimodality, variable feature sizes, and normalization. Furthermore, we empirically demonstrate that such a model can successfully estimate multiple features, including transmission rank, selected precoder, Doppler spread, and delay profile.

Group Think: Multiple Concurrent Reasoning Agents Collaborating at Token Level Granularity

Recent advances in large language models (LLMs) have demonstrated the power of reasoning through self-generated chains of thought. Multiple reasoning agents can collaborate to raise joint reasoning quality above individual outcomes. However, such agents typically interact in a turn-based manner, trading increased latency for improved quality. In this paper, we propose Group Think--a single LLM that acts as multiple concurrent reasoning agents, or thinkers. With shared visibility into each other's partial generation progress, Group Think introduces a new concurrent-reasoning paradigm in which multiple reasoning trajectories adapt dynamically to one another at the token level. For example, a reasoning thread may shift its generation mid-sentence upon detecting that another thread is better positioned to continue. This fine-grained, token-level collaboration enables Group Think to reduce redundant reasoning and improve quality while achieving significantly lower latency. Moreover, its concurrent nature allows for efficient utilization of idle computational resources, making it especially suitable for edge inference, where very small batch size often underutilizes local~GPUs. We give a simple and generalizable modification that enables any existing LLM to perform Group Think on a local GPU. We also present an evaluation strategy to benchmark reasoning latency and empirically demonstrate latency improvements using open-source LLMs that were not explicitly trained for Group Think. We hope this work paves the way for future LLMs to exhibit more sophisticated and more efficient collaborative behavior for higher quality generation.

Exact, Tractable Gauss-Newton Optimization in Deep Reversible Architectures Reveal Poor Generalization

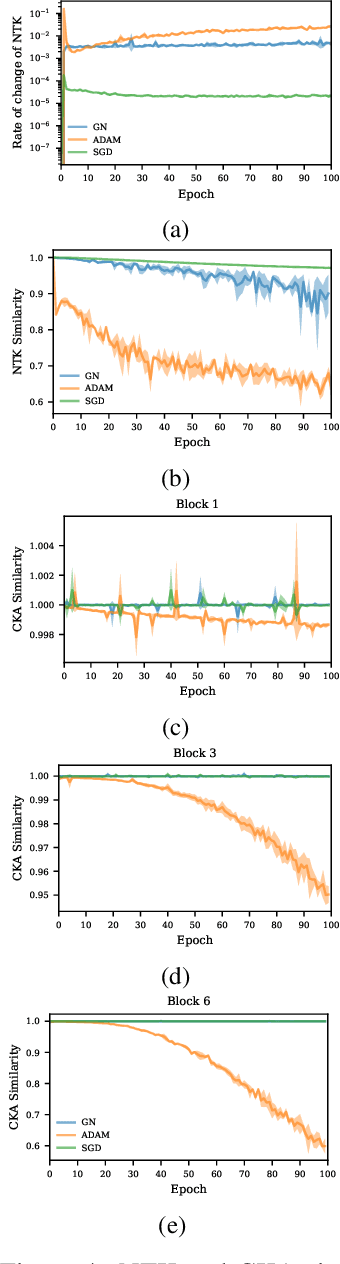
Second-order optimization has been shown to accelerate the training of deep neural networks in many applications, often yielding faster progress per iteration on the training loss compared to first-order optimizers. However, the generalization properties of second-order methods are still being debated. Theoretical investigations have proved difficult to carry out outside the tractable settings of heavily simplified model classes -- thus, the relevance of existing theories to practical deep learning applications remains unclear. Similarly, empirical studies in large-scale models and real datasets are significantly confounded by the necessity to approximate second-order updates in practice. It is often unclear whether the observed generalization behaviour arises specifically from the second-order nature of the parameter updates, or instead reflects the specific structured (e.g.\ Kronecker) approximations used or any damping-based interpolation towards first-order updates. Here, we show for the first time that exact Gauss-Newton (GN) updates take on a tractable form in a class of deep reversible architectures that are sufficiently expressive to be meaningfully applied to common benchmark datasets. We exploit this novel setting to study the training and generalization properties of the GN optimizer. We find that exact GN generalizes poorly. In the mini-batch training setting, this manifests as rapidly saturating progress even on the \emph{training} loss, with parameter updates found to overfit each mini-batchatch without producing the features that would support generalization to other mini-batches. We show that our experiments run in the ``lazy'' regime, in which the neural tangent kernel (NTK) changes very little during the course of training. This behaviour is associated with having no significant changes in neural representations, explaining the lack of generalization.

Deep Equilibrium Algorithmic Reasoning

Neural Algorithmic Reasoning (NAR) research has demonstrated that graph neural networks (GNNs) could learn to execute classical algorithms. However, most previous approaches have always used a recurrent architecture, where each iteration of the GNN matches an iteration of the algorithm. In this paper we study neurally solving algorithms from a different perspective: since the algorithm's solution is often an equilibrium, it is possible to find the solution directly by solving an equilibrium equation. Our approach requires no information on the ground-truth number of steps of the algorithm, both during train and test time. Furthermore, the proposed method improves the performance of GNNs on executing algorithms and is a step towards speeding up existing NAR models. Our empirical evidence, leveraging algorithms from the CLRS-30 benchmark, validates that one can train a network to solve algorithmic problems by directly finding the equilibrium. We discuss the practical implementation of such models and propose regularisations to improve the performance of these equilibrium reasoners.

CliquePH: Higher-Order Information for Graph Neural Networks through Persistent Homology on Clique Graphs

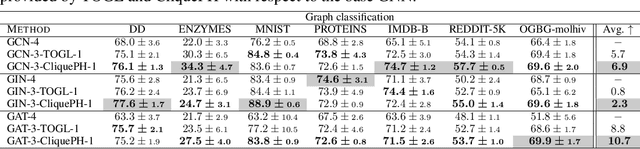
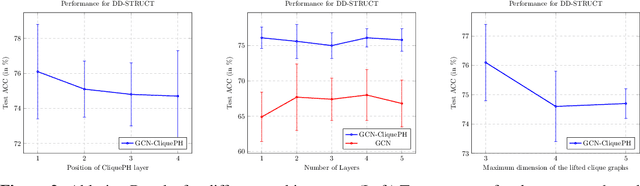
Graph neural networks have become the default choice by practitioners for graph learning tasks such as graph classification and node classification. Nevertheless, popular graph neural network models still struggle to capture higher-order information, i.e., information that goes \emph{beyond} pairwise interactions. Recent work has shown that persistent homology, a tool from topological data analysis, can enrich graph neural networks with topological information that they otherwise could not capture. Calculating such features is efficient for dimension 0 (connected components) and dimension 1 (cycles). However, when it comes to higher-order structures, it does not scale well, with a complexity of $O(n^d)$, where $n$ is the number of nodes and $d$ is the order of the structures. In this work, we introduce a novel method that extracts information about higher-order structures in the graph while still using the efficient low-dimensional persistent homology algorithm. On standard benchmark datasets, we show that our method can lead to up to $31\%$ improvements in test accuracy.

The Deep Equilibrium Algorithmic Reasoner

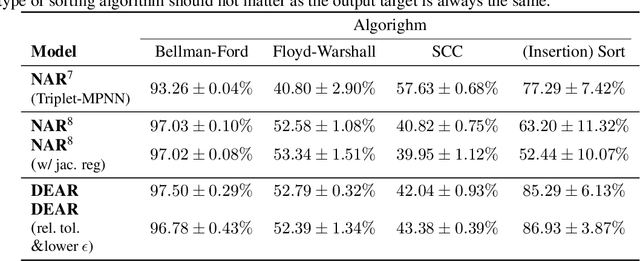
Recent work on neural algorithmic reasoning has demonstrated that graph neural networks (GNNs) could learn to execute classical algorithms. Doing so, however, has always used a recurrent architecture, where each iteration of the GNN aligns with an algorithm's iteration. Since an algorithm's solution is often an equilibrium, we conjecture and empirically validate that one can train a network to solve algorithmic problems by directly finding the equilibrium. Note that this does not require matching each GNN iteration with a step of the algorithm.

Is Meta-Learning the Right Approach for the Cold-Start Problem in Recommender Systems?

Recommender systems have become fundamental building blocks of modern online products and services, and have a substantial impact on user experience. In the past few years, deep learning methods have attracted a lot of research, and are now heavily used in modern real-world recommender systems. Nevertheless, dealing with recommendations in the cold-start setting, e.g., when a user has done limited interactions in the system, is a problem that remains far from solved. Meta-learning techniques, and in particular optimization-based meta-learning, have recently become the most popular approaches in the academic research literature for tackling the cold-start problem in deep learning models for recommender systems. However, current meta-learning approaches are not practical for real-world recommender systems, which have billions of users and items, and strict latency requirements. In this paper we show that it is possible to obtaining similar, or higher, performance on commonly used benchmarks for the cold-start problem without using meta-learning techniques. In more detail, we show that, when tuned correctly, standard and widely adopted deep learning models perform just as well as newer meta-learning models. We further show that an extremely simple modular approach using common representation learning techniques, can perform comparably to meta-learning techniques specifically designed for the cold-start setting while being much more easily deployable in real-world applications.

Extending Logic Explained Networks to Text Classification

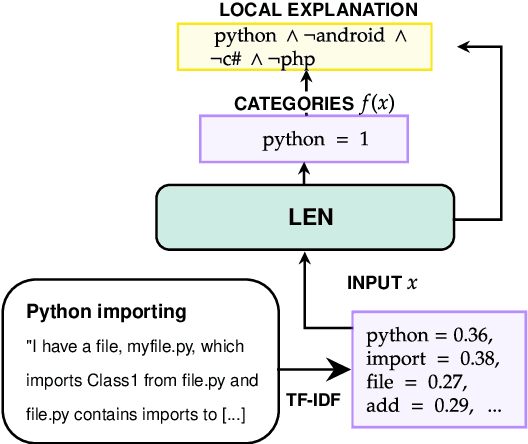
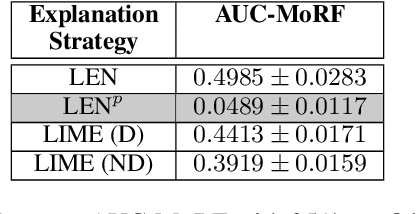
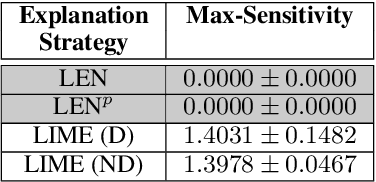
Recently, Logic Explained Networks (LENs) have been proposed as explainable-by-design neural models providing logic explanations for their predictions. However, these models have only been applied to vision and tabular data, and they mostly favour the generation of global explanations, while local ones tend to be noisy and verbose. For these reasons, we propose LENp, improving local explanations by perturbing input words, and we test it on text classification. Our results show that (i) LENp provides better local explanations than LIME in terms of sensitivity and faithfulness, and (ii) logic explanations are more useful and user-friendly than feature scoring provided by LIME as attested by a human survey.

Scalable Regularization of Scene Graph Generation Models using Symbolic Theories

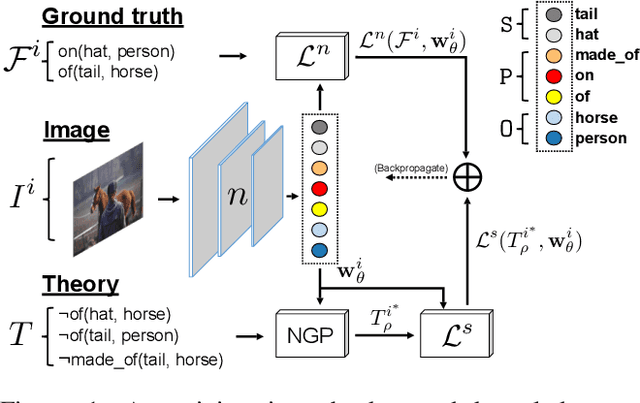
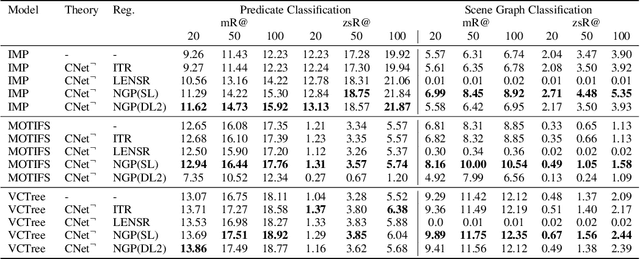
Several techniques have recently aimed to improve the performance of deep learning models for Scene Graph Generation (SGG) by incorporating background knowledge. State-of-the-art techniques can be divided into two families: one where the background knowledge is incorporated into the model in a subsymbolic fashion, and another in which the background knowledge is maintained in symbolic form. Despite promising results, both families of techniques face several shortcomings: the first one requires ad-hoc, more complex neural architectures increasing the training or inference cost; the second one suffers from limited scalability w.r.t. the size of the background knowledge. Our work introduces a regularization technique for injecting symbolic background knowledge into neural SGG models that overcomes the limitations of prior art. Our technique is model-agnostic, does not incur any cost at inference time, and scales to previously unmanageable background knowledge sizes. We demonstrate that our technique can improve the accuracy of state-of-the-art SGG models, by up to 33%.

SizeShiftReg: a Regularization Method for Improving Size-Generalization in Graph Neural Networks

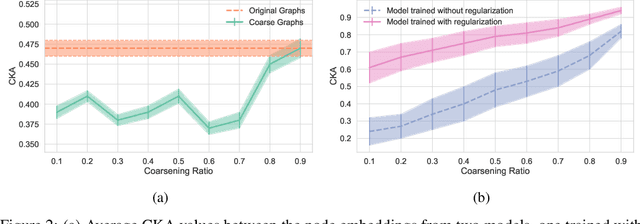
In the past few years, graph neural networks (GNNs) have become the de facto model of choice for graph classification. While, from the theoretical viewpoint, most GNNs can operate on graphs of any size, it is empirically observed that their classification performance degrades when they are applied on graphs with sizes that differ from those in the training data. Previous works have tried to tackle this issue in graph classification by providing the model with inductive biases derived from assumptions on the generative process of the graphs, or by requiring access to graphs from the test domain. The first strategy is tied to the use of ad-hoc models and to the quality of the assumptions made on the generative process, leaving open the question of how to improve the performance of generic GNN models in general settings. On the other hand, the second strategy can be applied to any GNN, but requires access to information that is not always easy to obtain. In this work we consider the scenario in which we only have access to the training data, and we propose a regularization strategy that can be applied to any GNN to improve its generalization capabilities from smaller to larger graphs without requiring access to the test data. Our regularization is based on the idea of simulating a shift in the size of the training graphs using coarsening techniques, and enforcing the model to be robust to such a shift. Experimental results on standard datasets show that popular GNN models, trained on the 50% smallest graphs in the dataset and tested on the 10% largest graphs, obtain performance improvements of up to 30% when trained with our regularization strategy.