Deep Equilibrium Algorithmic Reasoning

Neural Algorithmic Reasoning (NAR) research has demonstrated that graph neural networks (GNNs) could learn to execute classical algorithms. However, most previous approaches have always used a recurrent architecture, where each iteration of the GNN matches an iteration of the algorithm. In this paper we study neurally solving algorithms from a different perspective: since the algorithm's solution is often an equilibrium, it is possible to find the solution directly by solving an equilibrium equation. Our approach requires no information on the ground-truth number of steps of the algorithm, both during train and test time. Furthermore, the proposed method improves the performance of GNNs on executing algorithms and is a step towards speeding up existing NAR models. Our empirical evidence, leveraging algorithms from the CLRS-30 benchmark, validates that one can train a network to solve algorithmic problems by directly finding the equilibrium. We discuss the practical implementation of such models and propose regularisations to improve the performance of these equilibrium reasoners.

Cayley Graph Propagation

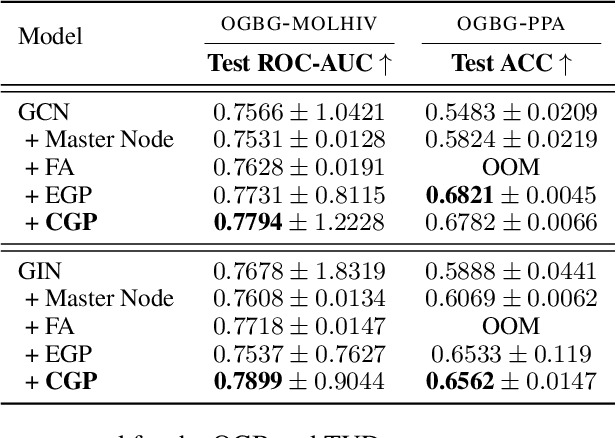
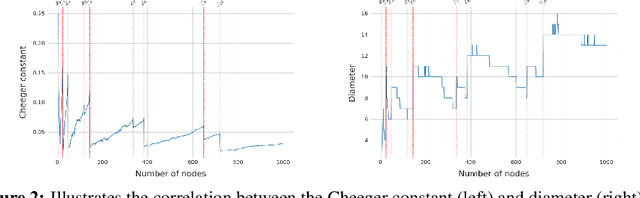
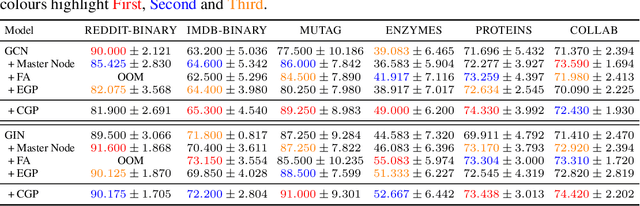
In spite of the plethora of success stories with graph neural networks (GNNs) on modelling graph-structured data, they are notoriously vulnerable to over-squashing, whereby tasks necessitate the mixing of information between distance pairs of nodes. To address this problem, prior work suggests rewiring the graph structure to improve information flow. Alternatively, a significant body of research has dedicated itself to discovering and precomputing bottleneck-free graph structures to ameliorate over-squashing. One well regarded family of bottleneck-free graphs within the mathematical community are expander graphs, with prior work$\unicode{x2014}$Expander Graph Propagation (EGP)$\unicode{x2014}$proposing the use of a well-known expander graph family$\unicode{x2014}$the Cayley graphs of the $\mathrm{SL}(2,\mathbb{Z}_n)$ special linear group$\unicode{x2014}$as a computational template for GNNs. However, in EGP the computational graphs used are truncated to align with a given input graph. In this work, we show that truncation is detrimental to the coveted expansion properties. Instead, we propose CGP, a method to propagate information over a complete Cayley graph structure, thereby ensuring it is bottleneck-free to better alleviate over-squashing. Our empirical evidence across several real-world datasets not only shows that CGP recovers significant improvements as compared to EGP, but it is also akin to or outperforms computationally complex graph rewiring techniques.