Wavelet-Induced Rotary Encodings: RoPE Meets Graphs

We introduce WIRE: Wavelet-Induced Rotary Encodings. WIRE extends Rotary Position Encodings (RoPE), a popular algorithm in LLMs and ViTs, to graph-structured data. We demonstrate that WIRE is more general than RoPE, recovering the latter in the special case of grid graphs. WIRE also enjoys a host of desirable theoretical properties, including equivariance under node ordering permutation, compatibility with linear attention, and (under select assumptions) asymptotic dependence on graph resistive distance. We test WIRE on a range of synthetic and real-world tasks, including identifying monochromatic subgraphs, semantic segmentation of point clouds, and more standard graph benchmarks. We find it to be effective in settings where the underlying graph structure is important.

KNARsack: Teaching Neural Algorithmic Reasoners to Solve Pseudo-Polynomial Problems

Neural algorithmic reasoning (NAR) is a growing field that aims to embed algorithmic logic into neural networks by imitating classical algorithms. In this extended abstract, we detail our attempt to build a neural algorithmic reasoner that can solve Knapsack, a pseudo-polynomial problem bridging classical algorithms and combinatorial optimisation, but omitted in standard NAR benchmarks. Our neural algorithmic reasoner is designed to closely follow the two-phase pipeline for the Knapsack problem, which involves first constructing the dynamic programming table and then reconstructing the solution from it. The approach, which models intermediate states through dynamic programming supervision, achieves better generalization to larger problem instances than a direct-prediction baseline that attempts to select the optimal subset only from the problem inputs.

What makes a good feedforward computational graph?

As implied by the plethora of literature on graph rewiring, the choice of computational graph employed by a neural network can make a significant impact on its downstream performance. Certain effects related to the computational graph, such as under-reaching and over-squashing, may even render the model incapable of learning certain functions. Most of these effects have only been thoroughly studied in the domain of undirected graphs; however, recent years have seen a significant rise in interest in feedforward computational graphs: directed graphs without any back edges. In this paper, we study the desirable properties of a feedforward computational graph, discovering two important complementary measures: fidelity and mixing time, and evaluating a few popular choices of graphs through the lens of these measures. Our study is backed by both theoretical analyses of the metrics' asymptotic behaviour for various graphs, as well as correlating these metrics to the performance of trained neural network models using the corresponding graphs.

Amplifying human performance in combinatorial competitive programming

Recent years have seen a significant surge in complex AI systems for competitive programming, capable of performing at admirable levels against human competitors. While steady progress has been made, the highest percentiles still remain out of reach for these methods on standard competition platforms such as Codeforces. Here we instead focus on combinatorial competitive programming, where the target is to find as-good-as-possible solutions to otherwise computationally intractable problems, over specific given inputs. We hypothesise that this scenario offers a unique testbed for human-AI synergy, as human programmers can write a backbone of a heuristic solution, after which AI can be used to optimise the scoring function used by the heuristic. We deploy our approach on previous iterations of Hash Code, a global team programming competition inspired by NP-hard software engineering problems at Google, and we leverage FunSearch to evolve our scoring functions. Our evolved solutions significantly improve the attained scores from their baseline, successfully breaking into the top percentile on all previous Hash Code online qualification rounds, and outperforming the top human teams on several. Our method is also performant on an optimisation problem that featured in a recent held-out AtCoder contest.

NAR-*ICP: Neural Execution of Classical ICP-based Pointcloud Registration Algorithms

This study explores the intersection of neural networks and classical robotics algorithms through the Neural Algorithmic Reasoning (NAR) framework, allowing to train neural networks to effectively reason like classical robotics algorithms by learning to execute them. Algorithms are integral to robotics and safety-critical applications due to their predictable and consistent performance through logical and mathematical principles. In contrast, while neural networks are highly adaptable, handling complex, high-dimensional data and generalising across tasks, they often lack interpretability and transparency in their internal computations. We propose a Graph Neural Network (GNN)-based learning framework, NAR-*ICP, which learns the intermediate algorithmic steps of classical ICP-based pointcloud registration algorithms, and extend the CLRS Algorithmic Reasoning Benchmark with classical robotics perception algorithms. We evaluate our approach across diverse datasets, from real-world to synthetic, demonstrating its flexibility in handling complex and noisy inputs, along with its potential to be used as part of a larger learning system. Our results indicate that our method achieves superior performance across all benchmarks and datasets, consistently surpassing even the algorithms it has been trained on, further demonstrating its ability to generalise beyond the capabilities of traditional algorithms.

Round and Round We Go! What makes Rotary Positional Encodings useful?

Positional Encodings (PEs) are a critical component of Transformer-based Large Language Models (LLMs), providing the attention mechanism with important sequence-position information. One of the most popular types of encoding used today in LLMs are Rotary Positional Encodings (RoPE), that rotate the queries and keys based on their relative distance. A common belief is that RoPE is useful because it helps to decay token dependency as relative distance increases. In this work, we argue that this is unlikely to be the core reason. We study the internals of a trained Gemma 7B model to understand how RoPE is being used at a mechanical level. We find that Gemma learns to use RoPE to construct robust "positional" attention patterns by exploiting the highest frequencies. We also find that, in general, Gemma greatly prefers to use the lowest frequencies of RoPE, which we suspect are used to carry semantic information. We mathematically prove interesting behaviours of RoPE and conduct experiments to verify our findings, proposing a modification of RoPE that fixes some highlighted issues and improves performance. We believe that this work represents an interesting step in better understanding PEs in LLMs, which we believe holds crucial value for scaling LLMs to large sizes and context lengths.

Cayley Graph Propagation

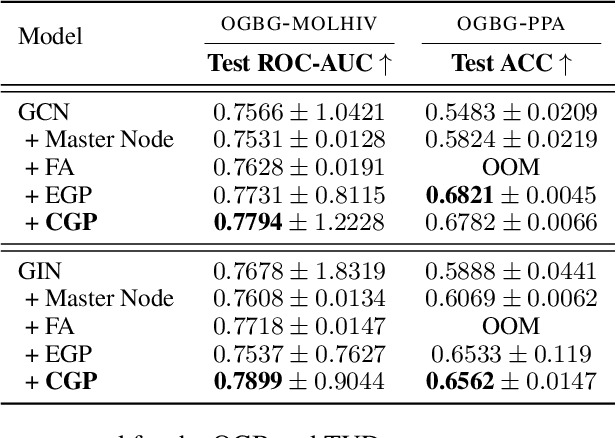
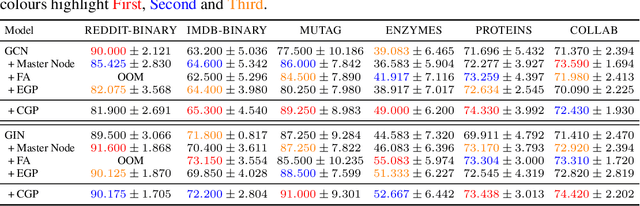
In spite of the plethora of success stories with graph neural networks (GNNs) on modelling graph-structured data, they are notoriously vulnerable to over-squashing, whereby tasks necessitate the mixing of information between distance pairs of nodes. To address this problem, prior work suggests rewiring the graph structure to improve information flow. Alternatively, a significant body of research has dedicated itself to discovering and precomputing bottleneck-free graph structures to ameliorate over-squashing. One well regarded family of bottleneck-free graphs within the mathematical community are expander graphs, with prior work$\unicode{x2014}$Expander Graph Propagation (EGP)$\unicode{x2014}$proposing the use of a well-known expander graph family$\unicode{x2014}$the Cayley graphs of the $\mathrm{SL}(2,\mathbb{Z}_n)$ special linear group$\unicode{x2014}$as a computational template for GNNs. However, in EGP the computational graphs used are truncated to align with a given input graph. In this work, we show that truncation is detrimental to the coveted expansion properties. Instead, we propose CGP, a method to propagate information over a complete Cayley graph structure, thereby ensuring it is bottleneck-free to better alleviate over-squashing. Our empirical evidence across several real-world datasets not only shows that CGP recovers significant improvements as compared to EGP, but it is also akin to or outperforms computationally complex graph rewiring techniques.

Positional Attention: Out-of-Distribution Generalization and Expressivity for Neural Algorithmic Reasoning

There has been a growing interest in the ability of neural networks to solve algorithmic tasks, such as arithmetic, summary statistics, and sorting. While state-of-the-art models like Transformers have demonstrated good generalization performance on in-distribution tasks, their out-of-distribution (OOD) performance is poor when trained end-to-end. In this paper, we focus on value generalization, a common instance of OOD generalization where the test distribution has the same input sequence length as the training distribution, but the value ranges in the training and test distributions do not necessarily overlap. To address this issue, we propose that using fixed positional encodings to determine attention weights-referred to as positional attention-enhances empirical OOD performance while maintaining expressivity. We support our claim about expressivity by proving that Transformers with positional attention can effectively simulate parallel algorithms.

softmax is not enough (for sharp out-of-distribution)

A key property of reasoning systems is the ability to make sharp decisions on their input data. For contemporary AI systems, a key carrier of sharp behaviour is the softmax function, with its capability to perform differentiable query-key lookups. It is a common belief that the predictive power of networks leveraging softmax arises from "circuits" which sharply perform certain kinds of computations consistently across many diverse inputs. However, for these circuits to be robust, they would need to generalise well to arbitrary valid inputs. In this paper, we dispel this myth: even for tasks as simple as finding the maximum key, any learned circuitry must disperse as the number of items grows at test time. We attribute this to a fundamental limitation of the softmax function to robustly approximate sharp functions, prove this phenomenon theoretically, and propose adaptive temperature as an ad-hoc technique for improving the sharpness of softmax at inference time.

Recurrent Aggregators in Neural Algorithmic Reasoning

Neural algorithmic reasoning (NAR) is an emerging field that seeks to design neural networks that mimic classical algorithmic computations. Today, graph neural networks (GNNs) are widely used in neural algorithmic reasoners due to their message passing framework and permutation equivariance. In this extended abstract, we challenge this design choice, and replace the equivariant aggregation function with a recurrent neural network. While seemingly counter-intuitive, this approach has appropriate grounding when nodes have a natural ordering -- and this is the case frequently in established reasoning benchmarks like CLRS-30. Indeed, our recurrent NAR (RNAR) model performs very strongly on such tasks, while handling many others gracefully. A notable achievement of RNAR is its decisive state-of-the-art result on the Heapsort and Quickselect tasks, both deemed as a significant challenge for contemporary neural algorithmic reasoners -- especially the latter, where RNAR achieves a mean micro-F1 score of 87%.