LVLM-COUNT: Enhancing the Counting Ability of Large Vision-Language Models

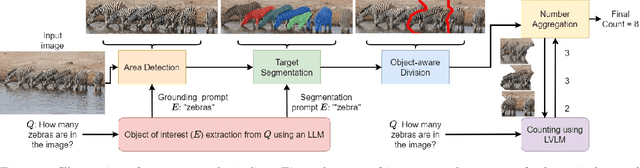
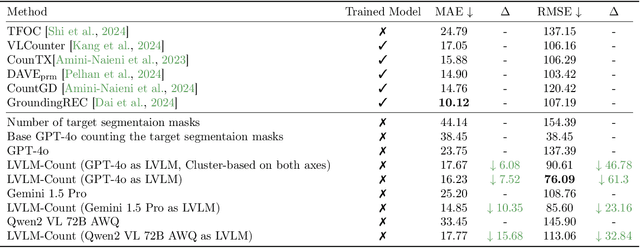
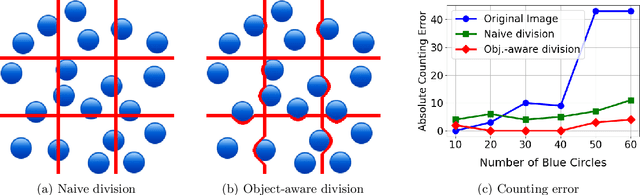
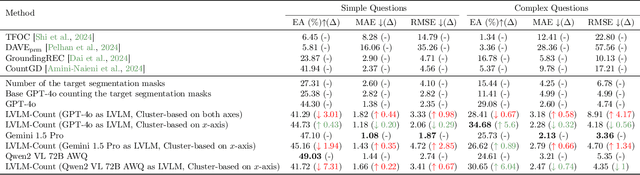
Counting is a fundamental skill for various visual tasks in real-life applications, requiring both object recognition and robust counting capabilities. Despite their advanced visual perception, large vision-language models (LVLMs) struggle with counting tasks, especially when the number of objects exceeds those commonly encountered during training. We enhance LVLMs' counting abilities using a divide-and-conquer approach, breaking counting problems into sub-counting tasks. Unlike prior methods, which do not generalize well to counting datasets on which they have not been trained, our method performs well on new datasets without any additional training or fine-tuning. We demonstrate that our approach enhances counting capabilities across various datasets and benchmarks.

Positional Attention: Out-of-Distribution Generalization and Expressivity for Neural Algorithmic Reasoning

There has been a growing interest in the ability of neural networks to solve algorithmic tasks, such as arithmetic, summary statistics, and sorting. While state-of-the-art models like Transformers have demonstrated good generalization performance on in-distribution tasks, their out-of-distribution (OOD) performance is poor when trained end-to-end. In this paper, we focus on value generalization, a common instance of OOD generalization where the test distribution has the same input sequence length as the training distribution, but the value ranges in the training and test distributions do not necessarily overlap. To address this issue, we propose that using fixed positional encodings to determine attention weights-referred to as positional attention-enhances empirical OOD performance while maintaining expressivity. We support our claim about expressivity by proving that Transformers with positional attention can effectively simulate parallel algorithms.

Analysis of Corrected Graph Convolutions

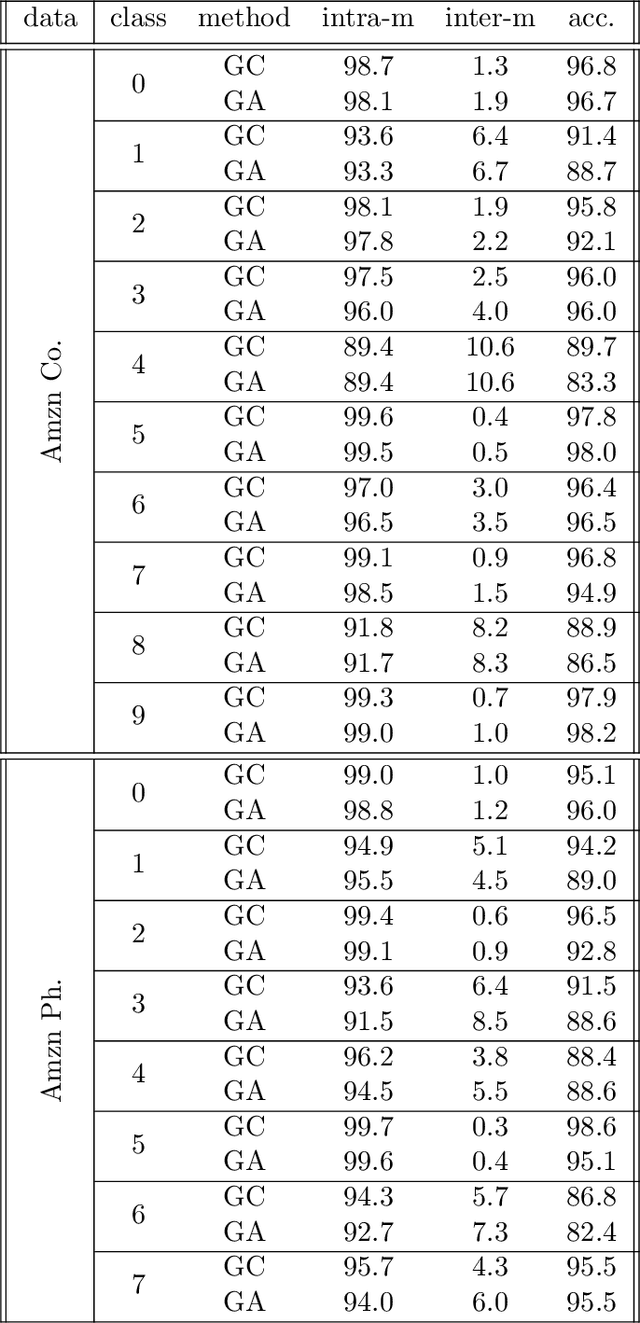
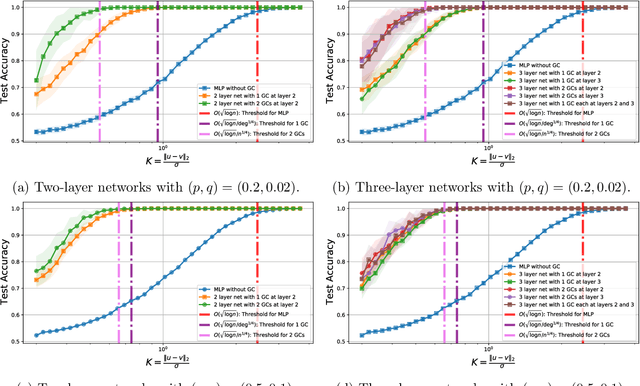
Machine learning for node classification on graphs is a prominent area driven by applications such as recommendation systems. State-of-the-art models often use multiple graph convolutions on the data, as empirical evidence suggests they can enhance performance. However, it has been shown empirically and theoretically, that too many graph convolutions can degrade performance significantly, a phenomenon known as oversmoothing. In this paper, we provide a rigorous theoretical analysis, based on the contextual stochastic block model (CSBM), of the performance of vanilla graph convolution from which we remove the principal eigenvector to avoid oversmoothing. We perform a spectral analysis for $k$ rounds of corrected graph convolutions, and we provide results for partial and exact classification. For partial classification, we show that each round of convolution can reduce the misclassification error exponentially up to a saturation level, after which performance does not worsen. For exact classification, we show that the separability threshold can be improved exponentially up to $O({\log{n}}/{\log\log{n}})$ corrected convolutions.

Simulation of Graph Algorithms with Looped Transformers

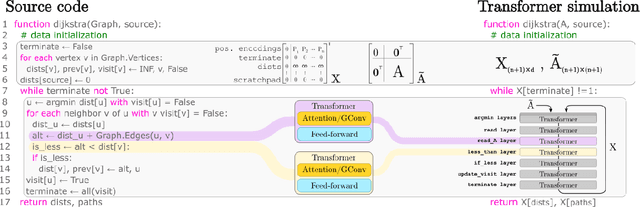
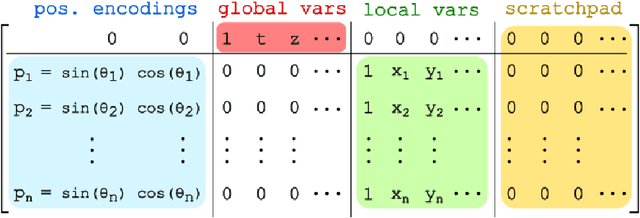
The execution of graph algorithms using neural networks has recently attracted significant interest due to promising empirical progress. This motivates further understanding of how neural networks can replicate reasoning steps with relational data. In this work, we study the ability of transformer networks to simulate algorithms on graphs from a theoretical perspective. The architecture that we utilize is a looped transformer with extra attention heads that interact with the graph. We prove by construction that this architecture can simulate algorithms such as Dijkstra's shortest path algorithm, Breadth- and Depth-First Search, and Kosaraju's strongly connected components algorithm. The width of the network does not increase with the size of the input graph, which implies that the network can simulate the above algorithms for any graph. Despite this property, we show that there is a limit to simulation in our solution due to finite precision. Finally, we show a Turing Completeness result with constant width when the extra attention heads are utilized.

Local Graph Clustering with Noisy Labels

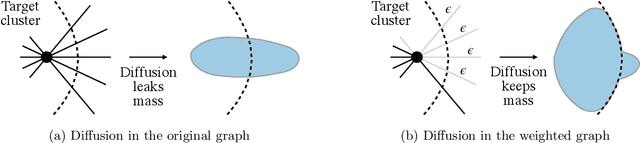
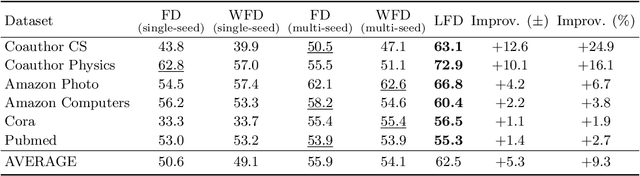
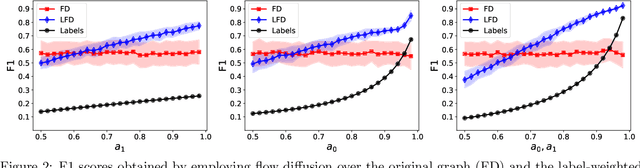
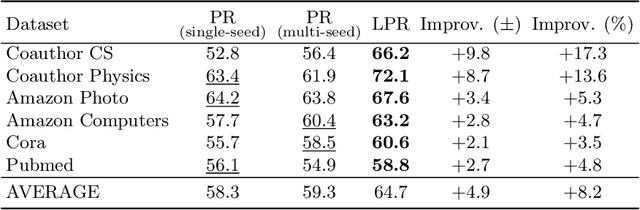
The growing interest in machine learning problems over graphs with additional node information such as texts, images, or labels has popularized methods that require the costly operation of processing the entire graph. Yet, little effort has been made to the development of fast local methods (i.e. without accessing the entire graph) that extract useful information from such data. To that end, we propose a study of local graph clustering using noisy node labels as a proxy for additional node information. In this setting, nodes receive initial binary labels based on cluster affiliation: 1 if they belong to the target cluster and 0 otherwise. Subsequently, a fraction of these labels is flipped. We investigate the benefits of incorporating noisy labels for local graph clustering. By constructing a weighted graph with such labels, we study the performance of graph diffusion-based local clustering method on both the original and the weighted graphs. From a theoretical perspective, we consider recovering an unknown target cluster with a single seed node in a random graph with independent noisy node labels. We provide sufficient conditions on the label noise under which, with high probability, using diffusion in the weighted graph yields a more accurate recovery of the target cluster. This approach proves more effective than using the given labels alone or using diffusion in the label-free original graph. Empirically, we show that reliable node labels can be obtained with just a few samples from an attributed graph. Moreover, utilizing these labels via diffusion in the weighted graph leads to significantly better local clustering performance across several real-world datasets, improving F1 scores by up to 13%.

Optimality of Message-Passing Architectures for Sparse Graphs

We study the node classification problem on feature-decorated graphs in the sparse setting, i.e., when the expected degree of a node is $O(1)$ in the number of nodes. Such graphs are typically known to be locally tree-like. We introduce a notion of Bayes optimality for node classification tasks, called asymptotic local Bayes optimality, and compute the optimal classifier according to this criterion for a fairly general statistical data model with arbitrary distributions of the node features and edge connectivity. The optimal classifier is implementable using a message-passing graph neural network architecture. We then compute the generalization error of this classifier and compare its performance against existing learning methods theoretically on a well-studied statistical model with naturally identifiable signal-to-noise ratios (SNRs) in the data. We find that the optimal message-passing architecture interpolates between a standard MLP in the regime of low graph signal and a typical convolution in the regime of high graph signal. Furthermore, we prove a corresponding non-asymptotic result.

On Classification Thresholds for Graph Attention with Edge Features

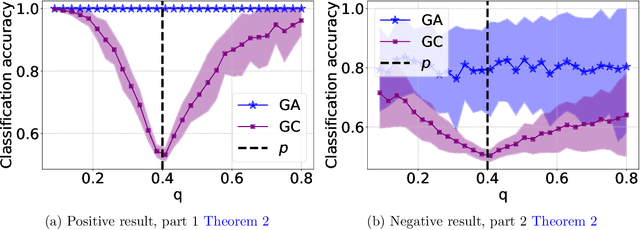
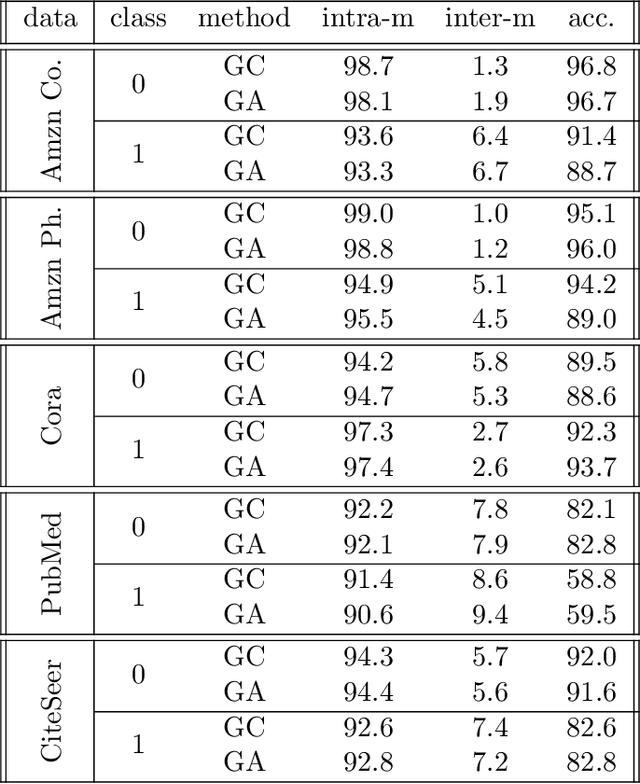
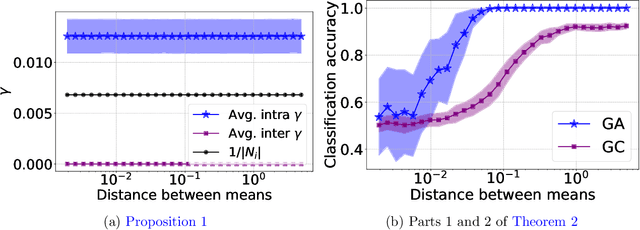
The recent years we have seen the rise of graph neural networks for prediction tasks on graphs. One of the dominant architectures is graph attention due to its ability to make predictions using weighted edge features and not only node features. In this paper we analyze, theoretically and empirically, graph attention networks and their ability of correctly labelling nodes in a classic classification task. More specifically, we study the performance of graph attention on the classic contextual stochastic block model (CSBM). In CSBM the nodes and edge features are obtained from a mixture of Gaussians and the edges from a stochastic block model. We consider a general graph attention mechanism that takes random edge features as input to determine the attention coefficients. We study two cases, in the first one, when the edge features are noisy, we prove that the majority of the attention coefficients are up to a constant uniform. This allows us to prove that graph attention with edge features is not better than simple graph convolution for achieving perfect node classification. Second, we prove that when the edge features are clean graph attention can distinguish intra- from inter-edges and this makes graph attention better than classic graph convolution.

Effects of Graph Convolutions in Deep Networks

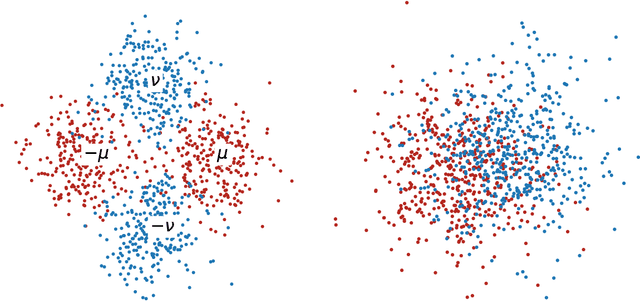
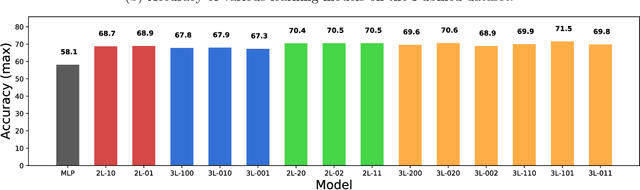
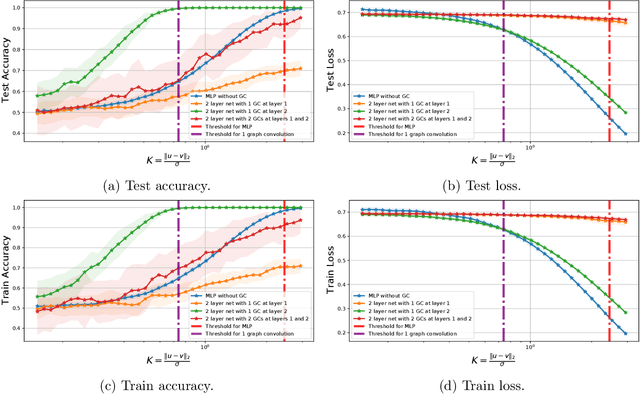
Graph Convolutional Networks (GCNs) are one of the most popular architectures that are used to solve classification problems accompanied by graphical information. We present a rigorous theoretical understanding of the effects of graph convolutions in multi-layer networks. We study these effects through the node classification problem of a non-linearly separable Gaussian mixture model coupled with a stochastic block model. First, we show that a single graph convolution expands the regime of the distance between the means where multi-layer networks can classify the data by a factor of at least $1/\sqrt[4]{\mathbb{E}{\rm deg}}$, where $\mathbb{E}{\rm deg}$ denotes the expected degree of a node. Second, we show that with a slightly stronger graph density, two graph convolutions improve this factor to at least $1/\sqrt[4]{n}$, where $n$ is the number of nodes in the graph. Finally, we provide both theoretical and empirical insights into the performance of graph convolutions placed in different combinations among the layers of a network, concluding that the performance is mutually similar for all combinations of the placement. We present extensive experiments on both synthetic and real-world data that illustrate our results.

Graph Attention Retrospective

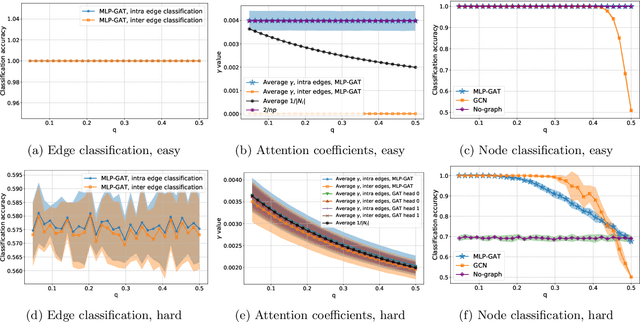
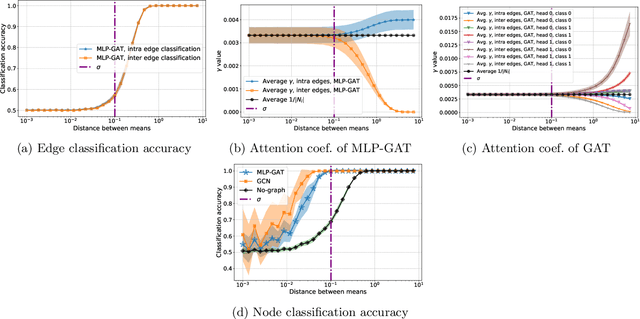
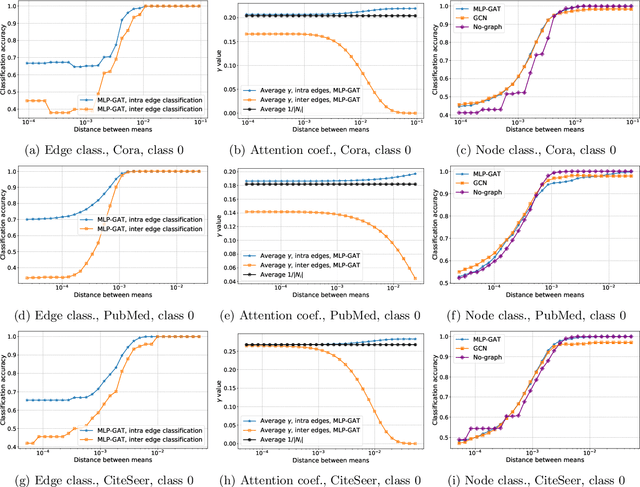
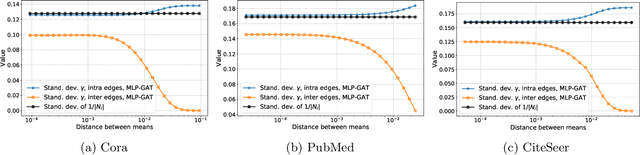
Graph-based learning is a rapidly growing sub-field of machine learning with applications in social networks, citation networks, and bioinformatics. One of the most popular type of models is graph attention networks. These models were introduced to allow a node to aggregate information from the features of neighbor nodes in a non-uniform way in contrast to simple graph convolution which does not distinguish the neighbors of a node. In this paper, we study theoretically this expected behaviour of graph attention networks. We prove multiple results on the performance of the graph attention mechanism for the problem of node classification for a contextual stochastic block model. Here the features of the nodes are obtained from a mixture of Gaussians and the edges from a stochastic block model where the features and the edges are coupled in a natural way. First, we show that in an "easy" regime, where the distance between the means of the Gaussians is large enough, graph attention maintains the weights of intra-class edges and significantly reduces the weights of the inter-class edges. As a corollary, we show that this implies perfect node classification independent of the weights of inter-class edges. However, a classical argument shows that in the "easy" regime, the graph is not needed at all to classify the data with high probability. In the "hard" regime, we show that every attention mechanism fails to distinguish intra-class from inter-class edges. We evaluate our theoretical results on synthetic and real-world data.

Local Hyper-flow Diffusion

A plethora of real-world problems require utilization of hypergraphs and diffusion algorithms. Examples include recommendation systems, node ranking in food networks and community detection in social networks to mention a few. Due to the increased size and complexity of real hypergraphs, local and accurate diffusion algorithms that work with the most complex hypergraphs are in need. We propose the first local diffusion method that works on higher-order relations with only a submodularity assumption. Our method is based on a primal-dual optimization formulation where the primal problem has a natural network flow interpretation, and the dual problem has a cut-based interpretation using the $\ell_2$-norm penalty for general submodular cut-costs. We prove that the proposed formulation achieves quadratic approximation error for the problem of local hypergraph clustering. We demonstrate that the new technique is significantly better than state-of-the-art methods over a range of real datasets for the local hypergraph clustering and node ranking problems.