Simulation of Graph Algorithms with Looped Transformers

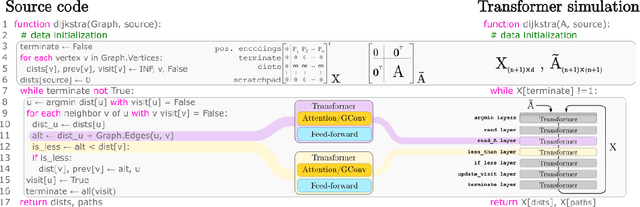
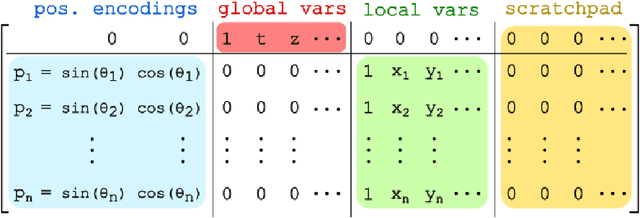
The execution of graph algorithms using neural networks has recently attracted significant interest due to promising empirical progress. This motivates further understanding of how neural networks can replicate reasoning steps with relational data. In this work, we study the ability of transformer networks to simulate algorithms on graphs from a theoretical perspective. The architecture that we utilize is a looped transformer with extra attention heads that interact with the graph. We prove by construction that this architecture can simulate algorithms such as Dijkstra's shortest path algorithm, Breadth- and Depth-First Search, and Kosaraju's strongly connected components algorithm. The width of the network does not increase with the size of the input graph, which implies that the network can simulate the above algorithms for any graph. Despite this property, we show that there is a limit to simulation in our solution due to finite precision. Finally, we show a Turing Completeness result with constant width when the extra attention heads are utilized.