Positional Attention: Out-of-Distribution Generalization and Expressivity for Neural Algorithmic Reasoning

There has been a growing interest in the ability of neural networks to solve algorithmic tasks, such as arithmetic, summary statistics, and sorting. While state-of-the-art models like Transformers have demonstrated good generalization performance on in-distribution tasks, their out-of-distribution (OOD) performance is poor when trained end-to-end. In this paper, we focus on value generalization, a common instance of OOD generalization where the test distribution has the same input sequence length as the training distribution, but the value ranges in the training and test distributions do not necessarily overlap. To address this issue, we propose that using fixed positional encodings to determine attention weights-referred to as positional attention-enhances empirical OOD performance while maintaining expressivity. We support our claim about expressivity by proving that Transformers with positional attention can effectively simulate parallel algorithms.

Simulation of Graph Algorithms with Looped Transformers

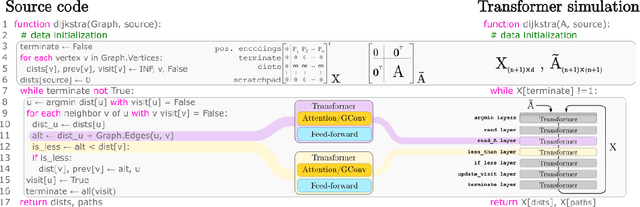
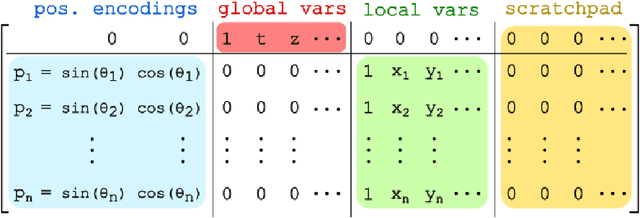
The execution of graph algorithms using neural networks has recently attracted significant interest due to promising empirical progress. This motivates further understanding of how neural networks can replicate reasoning steps with relational data. In this work, we study the ability of transformer networks to simulate algorithms on graphs from a theoretical perspective. The architecture that we utilize is a looped transformer with extra attention heads that interact with the graph. We prove by construction that this architecture can simulate algorithms such as Dijkstra's shortest path algorithm, Breadth- and Depth-First Search, and Kosaraju's strongly connected components algorithm. The width of the network does not increase with the size of the input graph, which implies that the network can simulate the above algorithms for any graph. Despite this property, we show that there is a limit to simulation in our solution due to finite precision. Finally, we show a Turing Completeness result with constant width when the extra attention heads are utilized.

Local Graph Clustering with Noisy Labels

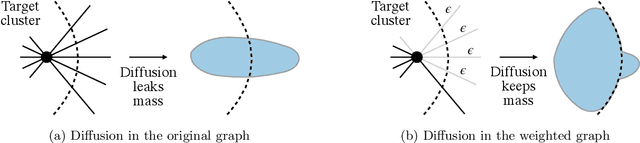
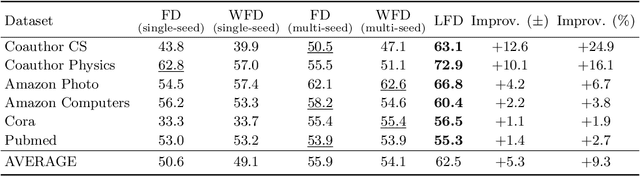
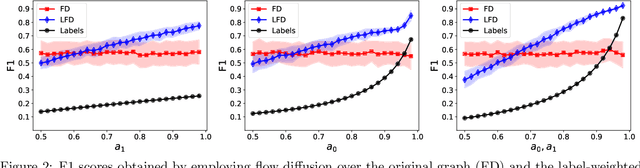
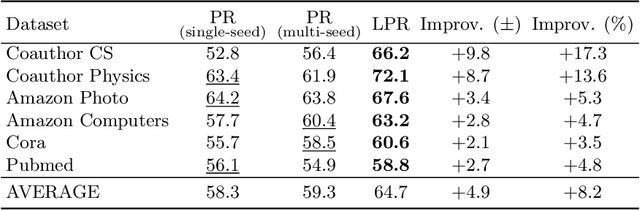
The growing interest in machine learning problems over graphs with additional node information such as texts, images, or labels has popularized methods that require the costly operation of processing the entire graph. Yet, little effort has been made to the development of fast local methods (i.e. without accessing the entire graph) that extract useful information from such data. To that end, we propose a study of local graph clustering using noisy node labels as a proxy for additional node information. In this setting, nodes receive initial binary labels based on cluster affiliation: 1 if they belong to the target cluster and 0 otherwise. Subsequently, a fraction of these labels is flipped. We investigate the benefits of incorporating noisy labels for local graph clustering. By constructing a weighted graph with such labels, we study the performance of graph diffusion-based local clustering method on both the original and the weighted graphs. From a theoretical perspective, we consider recovering an unknown target cluster with a single seed node in a random graph with independent noisy node labels. We provide sufficient conditions on the label noise under which, with high probability, using diffusion in the weighted graph yields a more accurate recovery of the target cluster. This approach proves more effective than using the given labels alone or using diffusion in the label-free original graph. Empirically, we show that reliable node labels can be obtained with just a few samples from an attributed graph. Moreover, utilizing these labels via diffusion in the weighted graph leads to significantly better local clustering performance across several real-world datasets, improving F1 scores by up to 13%.

Mitigating Data Heterogeneity in Federated Learning with Data Augmentation

Federated Learning (FL) is a prominent framework that enables training a centralized model while securing user privacy by fusing local, decentralized models. In this setting, one major obstacle is data heterogeneity, i.e., each client having non-identically and independently distributed (non-IID) data. This is analogous to the context of Domain Generalization (DG), where each client can be treated as a different domain. However, while many approaches in DG tackle data heterogeneity from the algorithmic perspective, recent evidence suggests that data augmentation can induce equal or greater performance. Motivated by this connection, we present federated versions of popular DG algorithms, and show that by applying appropriate data augmentation, we can mitigate data heterogeneity in the federated setting, and obtain higher accuracy on unseen clients. Equipped with data augmentation, we can achieve state-of-the-art performance using even the most basic Federated Averaging algorithm, with much sparser communication.