Activation Steering for Masked Diffusion Language Models

Masked diffusion language models (MDLMs) generate text through an iterative denoising process. They have recently gained attention due to mask-parallel decoding and competitive performance with autoregressive large language models. However, effective mechanisms for inference-time control and steering in MDLMs remain largely unexplored. We present an activation-steering framework for MDLMs that computes layer-wise steering vectors from a single forward pass using contrastive examples, without simulating the denoising trajectory. These directions are applied at every reverse-diffusion step, yielding an efficient inference-time control mechanism. Experiments on LLaDA-8B-Instruct demonstrate reliable modulation of high-level attributes, with ablations examining the effects of steering across transformer sub-modules and token scope (prompt vs.\ response).

Learnable Graph Convolutional Attention Networks

Existing Graph Neural Networks (GNNs) compute the message exchange between nodes by either aggregating uniformly (convolving) the features of all the neighboring nodes, or by applying a non-uniform score (attending) to the features. Recent works have shown the strengths and weaknesses of the resulting GNN architectures, respectively, GCNs and GATs. In this work, we aim at exploiting the strengths of both approaches to their full extent. To this end, we first introduce the graph convolutional attention layer (CAT), which relies on convolutions to compute the attention scores. Unfortunately, as in the case of GCNs and GATs, we show that there exists no clear winner between the three (neither theoretically nor in practice) as their performance directly depends on the nature of the data (i.e., of the graph and features). This result brings us to the main contribution of our work, the learnable graph convolutional attention network (L-CAT): a GNN architecture that automatically interpolates between GCN, GAT and CAT in each layer, by adding only two scalar parameters. Our results demonstrate that L-CAT is able to efficiently combine different GNN layers along the network, outperforming competing methods in a wide range of datasets, and resulting in a more robust model that reduces the need of cross-validating.

Graph Attention Retrospective

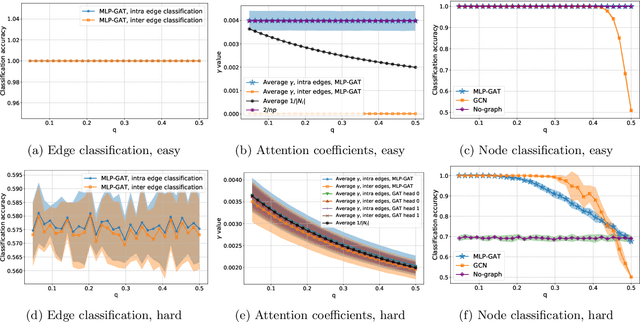
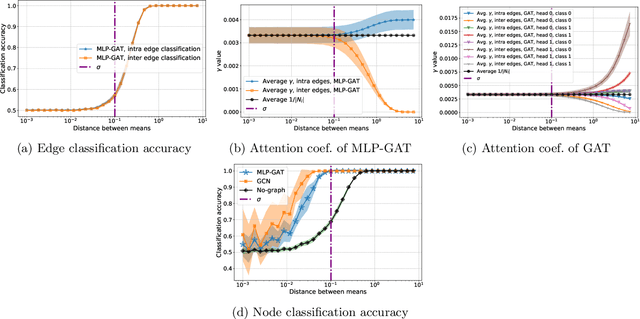
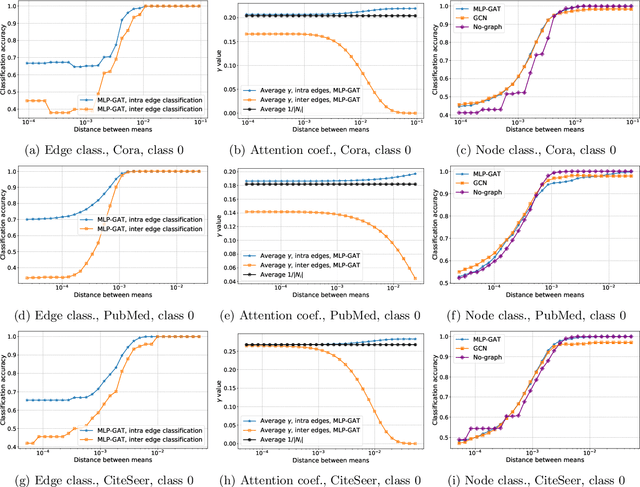
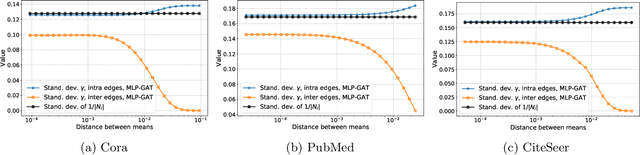
Graph-based learning is a rapidly growing sub-field of machine learning with applications in social networks, citation networks, and bioinformatics. One of the most popular type of models is graph attention networks. These models were introduced to allow a node to aggregate information from the features of neighbor nodes in a non-uniform way in contrast to simple graph convolution which does not distinguish the neighbors of a node. In this paper, we study theoretically this expected behaviour of graph attention networks. We prove multiple results on the performance of the graph attention mechanism for the problem of node classification for a contextual stochastic block model. Here the features of the nodes are obtained from a mixture of Gaussians and the edges from a stochastic block model where the features and the edges are coupled in a natural way. First, we show that in an "easy" regime, where the distance between the means of the Gaussians is large enough, graph attention maintains the weights of intra-class edges and significantly reduces the weights of the inter-class edges. As a corollary, we show that this implies perfect node classification independent of the weights of inter-class edges. However, a classical argument shows that in the "easy" regime, the graph is not needed at all to classify the data with high probability. In the "hard" regime, we show that every attention mechanism fails to distinguish intra-class from inter-class edges. We evaluate our theoretical results on synthetic and real-world data.

Learning and Testing Junta Distributions with Subcube Conditioning

We study the problems of learning and testing junta distributions on $\{-1,1\}^n$ with respect to the uniform distribution, where a distribution $p$ is a $k$-junta if its probability mass function $p(x)$ depends on a subset of at most $k$ variables. The main contribution is an algorithm for finding relevant coordinates in a $k$-junta distribution with subcube conditioning [BC18, CCKLW20]. We give two applications: 1. An algorithm for learning $k$-junta distributions with $\tilde{O}(k/\epsilon^2) \log n + O(2^k/\epsilon^2)$ subcube conditioning queries, and 2. An algorithm for testing $k$-junta distributions with $\tilde{O}((k + \sqrt{n})/\epsilon^2)$ subcube conditioning queries. All our algorithms are optimal up to poly-logarithmic factors. Our results show that subcube conditioning, as a natural model for accessing high-dimensional distributions, enables significant savings in learning and testing junta distributions compared to the standard sampling model. This addresses an open question posed by Aliakbarpour, Blais, and Rubinfeld [ABR17].

Random Restrictions of High-Dimensional Distributions and Uniformity Testing with Subcube Conditioning

We give a nearly-optimal algorithm for testing uniformity of distributions supported on $\{-1,1\}^n$, which makes $\tilde O (\sqrt{n}/\varepsilon^2)$ queries to a subcube conditional sampling oracle (Bhattacharyya and Chakraborty (2018)). The key technical component is a natural notion of random restriction for distributions on $\{-1,1\}^n$, and a quantitative analysis of how such a restriction affects the mean vector of the distribution. Along the way, we consider the problem of mean testing with independent samples and provide a nearly-optimal algorithm.