Causal normalizing flows: from theory to practice

In this work, we deepen on the use of normalizing flows for causal reasoning. Specifically, we first leverage recent results on non-linear ICA to show that causal models are identifiable from observational data given a causal ordering, and thus can be recovered using autoregressive normalizing flows (NFs). Second, we analyze different design and learning choices for causal normalizing flows to capture the underlying causal data-generating process. Third, we describe how to implement the do-operator in causal NFs, and thus, how to answer interventional and counterfactual questions. Finally, in our experiments, we validate our design and training choices through a comprehensive ablation study; compare causal NFs to other approaches for approximating causal models; and empirically demonstrate that causal NFs can be used to address real-world problems, where the presence of mixed discrete-continuous data and partial knowledge on the causal graph is the norm. The code for this work can be found at https://github.com/psanch21/causal-flows.

Learnable Graph Convolutional Attention Networks

Existing Graph Neural Networks (GNNs) compute the message exchange between nodes by either aggregating uniformly (convolving) the features of all the neighboring nodes, or by applying a non-uniform score (attending) to the features. Recent works have shown the strengths and weaknesses of the resulting GNN architectures, respectively, GCNs and GATs. In this work, we aim at exploiting the strengths of both approaches to their full extent. To this end, we first introduce the graph convolutional attention layer (CAT), which relies on convolutions to compute the attention scores. Unfortunately, as in the case of GCNs and GATs, we show that there exists no clear winner between the three (neither theoretically nor in practice) as their performance directly depends on the nature of the data (i.e., of the graph and features). This result brings us to the main contribution of our work, the learnable graph convolutional attention network (L-CAT): a GNN architecture that automatically interpolates between GCN, GAT and CAT in each layer, by adding only two scalar parameters. Our results demonstrate that L-CAT is able to efficiently combine different GNN layers along the network, outperforming competing methods in a wide range of datasets, and resulting in a more robust model that reduces the need of cross-validating.

Mitigating Modality Collapse in Multimodal VAEs via Impartial Optimization

A number of variational autoencoders (VAEs) have recently emerged with the aim of modeling multimodal data, e.g., to jointly model images and their corresponding captions. Still, multimodal VAEs tend to focus solely on a subset of the modalities, e.g., by fitting the image while neglecting the caption. We refer to this limitation as modality collapse. In this work, we argue that this effect is a consequence of conflicting gradients during multimodal VAE training. We show how to detect the sub-graphs in the computational graphs where gradients conflict (impartiality blocks), as well as how to leverage existing gradient-conflict solutions from multitask learning to mitigate modality collapse. That is, to ensure impartial optimization across modalities. We apply our training framework to several multimodal VAE models, losses and datasets from the literature, and empirically show that our framework significantly improves the reconstruction performance, conditional generation, and coherence of the latent space across modalities.

Rotograd: Dynamic Gradient Homogenization for Multi-Task Learning

While multi-task learning (MTL) has been successfully applied in several domains, it still triggers challenges. As a consequence of negative transfer, simultaneously learning several tasks can lead to unexpectedly poor results. A key factor contributing to this undesirable behavior is the problem of conflicting gradients. In this paper, we propose a novel approach for MTL, Rotograd, which homogenizes the gradient directions across all tasks by rotating their shared representation. Our algorithm is formalized as a Stackelberg game, which allows us to provide stability guarantees. Rotograd can be transparently combined with task-weighting approaches (e.g., GradNorm) to mitigate negative transfer, resulting in a robust learning process. Thorough empirical evaluation on several architectures (e.g., ResNet) and datasets (e.g., CIFAR) verifies our theoretical results, and shows that Rotograd outperforms previous approaches. A Pytorch implementation can be found in https://github.com/adrianjav/rotograd .

Relative gradient optimization of the Jacobian term in unsupervised deep learning

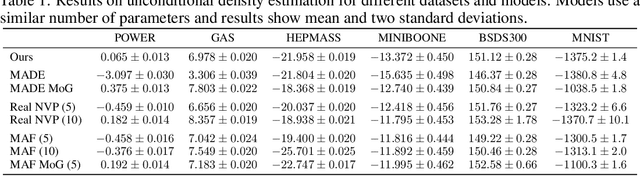
Learning expressive probabilistic models correctly describing the data is a ubiquitous problem in machine learning. A popular approach for solving it is mapping the observations into a representation space with a simple joint distribution, which can typically be written as a product of its marginals -- thus drawing a connection with the field of nonlinear independent component analysis. Deep density models have been widely used for this task, but their likelihood-based training requires estimating the log-determinant of the Jacobian and is computationally expensive, thus imposing a trade-off between computation and expressive power. In this work, we propose a new approach for exact likelihood-based training of such neural networks. Based on relative gradients, we exploit the matrix structure of neural network parameters to compute updates efficiently even in high-dimensional spaces; the computational cost of the training is quadratic in the input size, in contrast with the cubic scaling of the naive approaches. This allows fast training with objective functions involving the log-determinant of the Jacobian without imposing constraints on its structure, in stark contrast to normalizing flows. An implementation of our method can be found at https://github.com/fissoreg/relative-gradient-jacobian

Lipschitz standardization for robust multivariate learning

Current trends in machine learning rely on out-of-the-box gradient-based approaches. With the aim of mitigating numerical errors and to improve the convergence of the learning process, a common empirical practice is to standardize or normalize the data. However, there is a lack of theoretical analysis regarding why and when these methods result in an improvement of the learning process. In this work, we first study these methods in the context of black-box variational inference, specifically analyzing the effect that scaling the data has on the smoothness of the optimization landscape. Our analysis shows that no general rule applies in order to decide which of the existing data scaling methods, or even if they, will improve the learning process. Second, we highlight the issues that arise when dealing with multivariate data, due to the discrepancy in smoothness of the likelihood functions for different variables, and the inability to scale discrete data. Finally, we propose a novel Lipschitz standardization, and its extension for discrete data, which overcomes the aforementioned limitations. Specifically, as backed by our experiments, Lipschitz standardization i) favors a fairer learning across different variables in the data; and ii) results in faster and more accurate learning.