All or None: Identifiable Linear Properties of Next-token Predictors in Language Modeling

We analyze identifiability as a possible explanation for the ubiquity of linear properties across language models, such as the vector difference between the representations of "easy" and "easiest" being parallel to that between "lucky" and "luckiest". For this, we ask whether finding a linear property in one model implies that any model that induces the same distribution has that property, too. To answer that, we first prove an identifiability result to characterize distribution-equivalent next-token predictors, lifting a diversity requirement of previous results. Second, based on a refinement of relational linearity [Paccanaro and Hinton, 2001; Hernandez et al., 2024], we show how many notions of linearity are amenable to our analysis. Finally, we show that under suitable conditions, these linear properties either hold in all or none distribution-equivalent next-token predictors.

Independent Mechanism Analysis and the Manifold Hypothesis

Independent Mechanism Analysis (IMA) seeks to address non-identifiability in nonlinear Independent Component Analysis (ICA) by assuming that the Jacobian of the mixing function has orthogonal columns. As typical in ICA, previous work focused on the case with an equal number of latent components and observed mixtures. Here, we extend IMA to settings with a larger number of mixtures that reside on a manifold embedded in a higher-dimensional than the latent space -- in line with the manifold hypothesis in representation learning. For this setting, we show that IMA still circumvents several non-identifiability issues, suggesting that it can also be a beneficial principle for higher-dimensional observations when the manifold hypothesis holds. Further, we prove that the IMA principle is approximately satisfied with high probability (increasing with the number of observed mixtures) when the directions along which the latent components influence the observations are chosen independently at random. This provides a new and rigorous statistical interpretation of IMA.

CLadder: A Benchmark to Assess Causal Reasoning Capabilities of Language Models

The ability to perform causal reasoning is widely considered a core feature of intelligence. In this work, we investigate whether large language models (LLMs) can coherently reason about causality. Much of the existing work in natural language processing (NLP) focuses on evaluating commonsense causal reasoning in LLMs, thus failing to assess whether a model can perform causal inference in accordance with a set of well-defined formal rules. To address this, we propose a new NLP task, causal inference in natural language, inspired by the "causal inference engine" postulated by Judea Pearl et al. We compose a large dataset, CLadder, with 10K samples: based on a collection of causal graphs and queries (associational, interventional, and counterfactual), we obtain symbolic questions and ground-truth answers, through an oracle causal inference engine. These are then translated into natural language. We evaluate multiple LLMs on our dataset, and we introduce and evaluate a bespoke chain-of-thought prompting strategy, CausalCoT. We show that our task is highly challenging for LLMs, and we conduct an in-depth analysis to gain deeper insight into the causal reasoning abilities of LLMs. Our data is open-sourced at https://huggingface.co/datasets/causalNLP/cladder, and our code can be found at https://github.com/causalNLP/cladder.

Nonparametric Identifiability of Causal Representations from Unknown Interventions

We study causal representation learning, the task of inferring latent causal variables and their causal relations from high-dimensional functions ("mixtures") of the variables. Prior work relies on weak supervision, in the form of counterfactual pre- and post-intervention views or temporal structure; places restrictive assumptions, such as linearity, on the mixing function or latent causal model; or requires partial knowledge of the generative process, such as the causal graph or the intervention targets. We instead consider the general setting in which both the causal model and the mixing function are nonparametric. The learning signal takes the form of multiple datasets, or environments, arising from unknown interventions in the underlying causal model. Our goal is to identify both the ground truth latents and their causal graph up to a set of ambiguities which we show to be irresolvable from interventional data. We study the fundamental setting of two causal variables and prove that the observational distribution and one perfect intervention per node suffice for identifiability, subject to a genericity condition. This condition rules out spurious solutions that involve fine-tuning of the intervened and observational distributions, mirroring similar conditions for nonlinear cause-effect inference. For an arbitrary number of variables, we show that two distinct paired perfect interventions per node guarantee identifiability. Further, we demonstrate that the strengths of causal influences among the latent variables are preserved by all equivalent solutions, rendering the inferred representation appropriate for drawing causal conclusions from new data. Our study provides the first identifiability results for the general nonparametric setting with unknown interventions, and elucidates what is possible and impossible for causal representation learning without more direct supervision.

Causal Component Analysis

Independent Component Analysis (ICA) aims to recover independent latent variables from observed mixtures thereof. Causal Representation Learning (CRL) aims instead to infer causally related (thus often statistically dependent) latent variables, together with the unknown graph encoding their causal relationships. We introduce an intermediate problem termed Causal Component Analysis (CauCA). CauCA can be viewed as a generalization of ICA, modelling the causal dependence among the latent components, and as a special case of CRL. In contrast to CRL, it presupposes knowledge of the causal graph, focusing solely on learning the unmixing function and the causal mechanisms. Any impossibility results regarding the recovery of the ground truth in CauCA also apply for CRL, while possibility results may serve as a stepping stone for extensions to CRL. We characterize CauCA identifiability from multiple datasets generated through different types of interventions on the latent causal variables. As a corollary, this interventional perspective also leads to new identifiability results for nonlinear ICA -- a special case of CauCA with an empty graph -- requiring strictly fewer datasets than previous results. We introduce a likelihood-based approach using normalizing flows to estimate both the unmixing function and the causal mechanisms, and demonstrate its effectiveness through extensive synthetic experiments in the CauCA and ICA setting.

Evaluating vaccine allocation strategies using simulation-assisted causal modelling

Early on during a pandemic, vaccine availability is limited, requiring prioritisation of different population groups. Evaluating vaccine allocation is therefore a crucial element of pandemics response. In the present work, we develop a model to retrospectively evaluate age-dependent counterfactual vaccine allocation strategies against the COVID-19 pandemic. To estimate the effect of allocation on the expected severe-case incidence, we employ a simulation-assisted causal modelling approach which combines a compartmental infection-dynamics simulation, a coarse-grained, data-driven causal model and literature estimates for immunity waning. We compare Israel's implemented vaccine allocation strategy in 2021 to counterfactual strategies such as no prioritisation, prioritisation of younger age groups or a strict risk-ranked approach; we find that Israel's implemented strategy was indeed highly effective. We also study the marginal impact of increasing vaccine uptake for a given age group and find that increasing vaccinations in the elderly is most effective at preventing severe cases, whereas additional vaccinations for middle-aged groups reduce infections most effectively. Due to its modular structure, our model can easily be adapted to study future pandemics. We demonstrate this flexibility by investigating vaccine allocation strategies for a pandemic with characteristics of the Spanish Flu. Our approach thus helps evaluate vaccination strategies under the complex interplay of core epidemic factors, including age-dependent risk profiles, immunity waning, vaccine availability and spreading rates.

Probing the Robustness of Independent Mechanism Analysis for Representation Learning

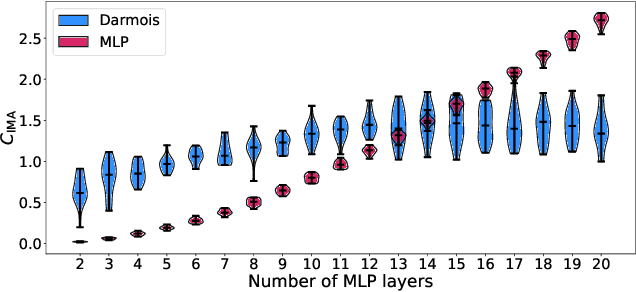
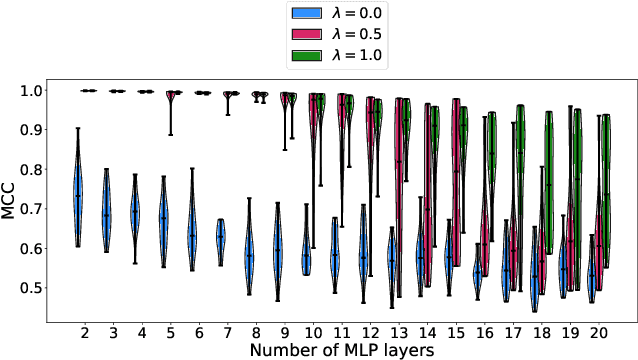
One aim of representation learning is to recover the original latent code that generated the data, a task which requires additional information or inductive biases. A recently proposed approach termed Independent Mechanism Analysis (IMA) postulates that each latent source should influence the observed mixtures independently, complementing standard nonlinear independent component analysis, and taking inspiration from the principle of independent causal mechanisms. While it was shown in theory and experiments that IMA helps recovering the true latents, the method's performance was so far only characterized when the modeling assumptions are exactly satisfied. Here, we test the method's robustness to violations of the underlying assumptions. We find that the benefits of IMA-based regularization for recovering the true sources extend to mixing functions with various degrees of violation of the IMA principle, while standard regularizers do not provide the same merits. Moreover, we show that unregularized maximum likelihood recovers mixing functions which systematically deviate from the IMA principle, and provide an argument elucidating the benefits of IMA-based regularization.

Embrace the Gap: VAEs Perform Independent Mechanism Analysis

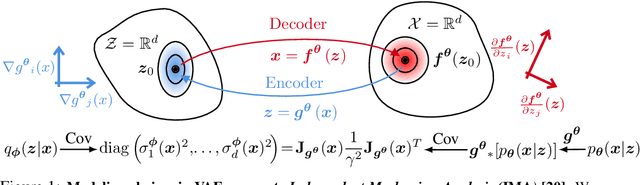
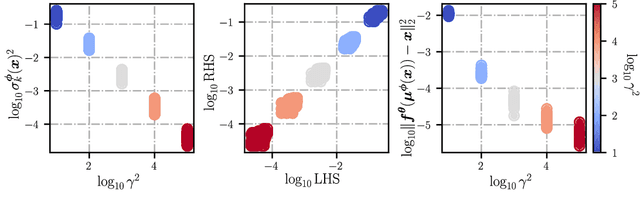
Variational autoencoders (VAEs) are a popular framework for modeling complex data distributions; they can be efficiently trained via variational inference by maximizing the evidence lower bound (ELBO), at the expense of a gap to the exact (log-)marginal likelihood. While VAEs are commonly used for representation learning, it is unclear why ELBO maximization would yield useful representations, since unregularized maximum likelihood estimation cannot invert the data-generating process. Yet, VAEs often succeed at this task. We seek to elucidate this apparent paradox by studying nonlinear VAEs in the limit of near-deterministic decoders. We first prove that, in this regime, the optimal encoder approximately inverts the decoder -- a commonly used but unproven conjecture -- which we refer to as {\em self-consistency}. Leveraging self-consistency, we show that the ELBO converges to a regularized log-likelihood. This allows VAEs to perform what has recently been termed independent mechanism analysis (IMA): it adds an inductive bias towards decoders with column-orthogonal Jacobians, which helps recovering the true latent factors. The gap between ELBO and log-likelihood is therefore welcome, since it bears unanticipated benefits for nonlinear representation learning. In experiments on synthetic and image data, we show that VAEs uncover the true latent factors when the data generating process satisfies the IMA assumption.

On Pitfalls of Identifiability in Unsupervised Learning. A Note on: "Desiderata for Representation Learning: A Causal Perspective"

Model identifiability is a desirable property in the context of unsupervised representation learning. In absence thereof, different models may be observationally indistinguishable while yielding representations that are nontrivially related to one another, thus making the recovery of a ground truth generative model fundamentally impossible, as often shown through suitably constructed counterexamples. In this note, we discuss one such construction, illustrating a potential failure case of an identifiability result presented in "Desiderata for Representation Learning: A Causal Perspective" by Wang & Jordan (2021). The construction is based on the theory of nonlinear independent component analysis. We comment on implications of this and other counterexamples for identifiable representation learning.

Causal Inference Through the Structural Causal Marginal Problem

We introduce an approach to counterfactual inference based on merging information from multiple datasets. We consider a causal reformulation of the statistical marginal problem: given a collection of marginal structural causal models (SCMs) over distinct but overlapping sets of variables, determine the set of joint SCMs that are counterfactually consistent with the marginal ones. We formalise this approach for categorical SCMs using the response function formulation and show that it reduces the space of allowed marginal and joint SCMs. Our work thus highlights a new mode of falsifiability through additional variables, in contrast to the statistical one via additional data.