David M. Blei
Bayesian Empirical Bayes: Simultaneous Inference from Probabilistic Symmetries
Dec 22, 2025
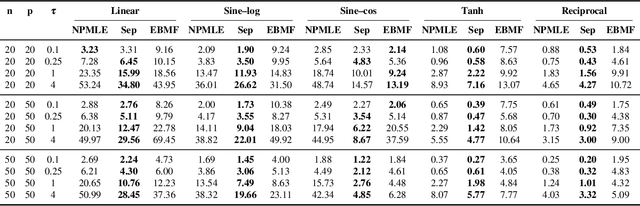

Abstract:Empirical Bayes (EB) improves the accuracy of simultaneous inference "by learning from the experience of others" (Efron, 2012). Classical EB theory focuses on latent variables that are iid draws from a fitted prior (Efron, 2019). Modern applications, however, feature complex structure, like arrays, spatial processes, or covariates. How can we apply EB ideas to these settings? We propose a generalized approach to empirical Bayes based on the notion of probabilistic symmetry. Our method pairs a simultaneous inference problem-with an unknown prior-to a symmetry assumption on the joint distribution of the latent variables. Each symmetry implies an ergodic decomposition, which we use to derive a corresponding empirical Bayes method. We call this methodBayesian empirical Bayes (BEB). We show how BEB recovers the classical methods of empirical Bayes, which implicitly assume exchangeability. We then use it to extend EB to other probabilistic symmetries: (i) EB matrix recovery for arrays and graphs; (ii) covariate-assisted EB for conditional data; (iii) EB spatial regression under shift invariance. We develop scalable algorithms based on variational inference and neural networks. In simulations, BEB outperforms existing approaches to denoising arrays and spatial data. On real data, we demonstrate BEB by denoising a cancer gene-expression matrix and analyzing spatial air-quality data from New York City.
Fisher meets Feynman: score-based variational inference with a product of experts
Oct 24, 2025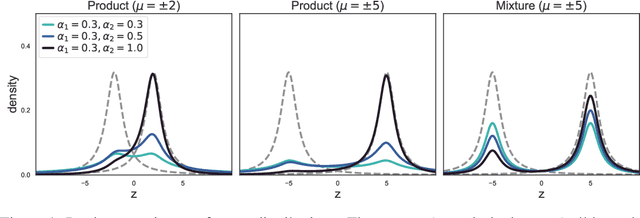
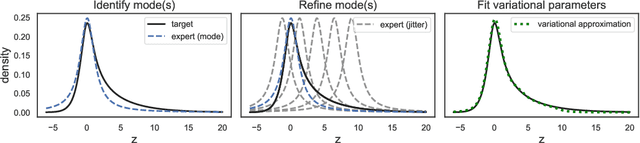
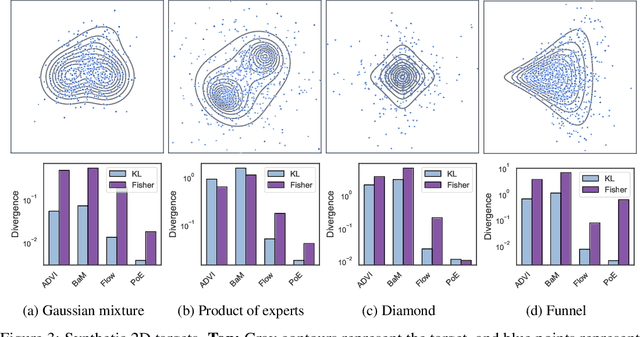
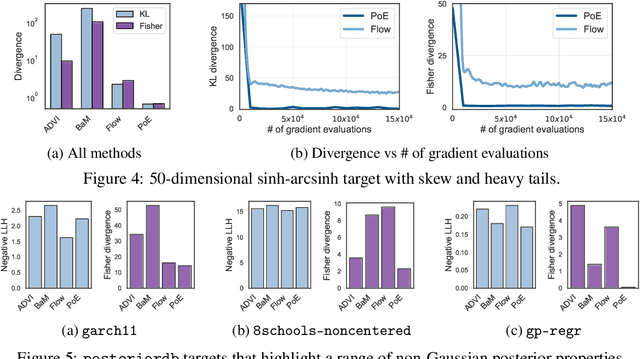
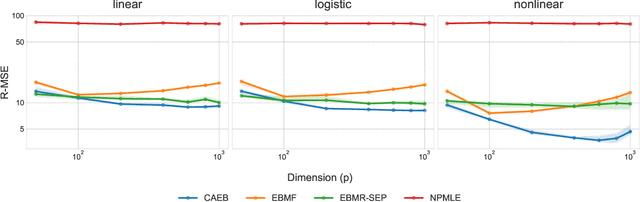
Abstract:We introduce a highly expressive yet distinctly tractable family for black-box variational inference (BBVI). Each member of this family is a weighted product of experts (PoE), and each weighted expert in the product is proportional to a multivariate $t$-distribution. These products of experts can model distributions with skew, heavy tails, and multiple modes, but to use them for BBVI, we must be able to sample from their densities. We show how to do this by reformulating these products of experts as latent variable models with auxiliary Dirichlet random variables. These Dirichlet variables emerge from a Feynman identity, originally developed for loop integrals in quantum field theory, that expresses the product of multiple fractions (or in our case, $t$-distributions) as an integral over the simplex. We leverage this simplicial latent space to draw weighted samples from these products of experts -- samples which BBVI then uses to find the PoE that best approximates a target density. Given a collection of experts, we derive an iterative procedure to optimize the exponents that determine their geometric weighting in the PoE. At each iteration, this procedure minimizes a regularized Fisher divergence to match the scores of the variational and target densities at a batch of samples drawn from the current approximation. This minimization reduces to a convex quadratic program, and we prove under general conditions that these updates converge exponentially fast to a near-optimal weighting of experts. We conclude by evaluating this approach on a variety of synthetic and real-world target distributions.
Adaptive Nonparametric Perturbations of Parametric Bayesian Models
Dec 17, 2024



Abstract:Parametric Bayesian modeling offers a powerful and flexible toolbox for scientific data analysis. Yet the model, however detailed, may still be wrong, and this can make inferences untrustworthy. In this paper we study nonparametrically perturbed parametric (NPP) Bayesian models, in which a parametric Bayesian model is relaxed via a distortion of its likelihood. We analyze the properties of NPP models when the target of inference is the true data distribution or some functional of it, such as in causal inference. We show that NPP models can offer the robustness of nonparametric models while retaining the data efficiency of parametric models, achieving fast convergence when the parametric model is close to true. To efficiently analyze data with an NPP model, we develop a generalized Bayes procedure to approximate its posterior. We demonstrate our method by estimating causal effects of gene expression from single cell RNA sequencing data. NPP modeling offers an efficient approach to robust Bayesian inference and can be used to robustify any parametric Bayesian model.
EigenVI: score-based variational inference with orthogonal function expansions
Oct 31, 2024Abstract:We develop EigenVI, an eigenvalue-based approach for black-box variational inference (BBVI). EigenVI constructs its variational approximations from orthogonal function expansions. For distributions over $\mathbb{R}^D$, the lowest order term in these expansions provides a Gaussian variational approximation, while higher-order terms provide a systematic way to model non-Gaussianity. These approximations are flexible enough to model complex distributions (multimodal, asymmetric), but they are simple enough that one can calculate their low-order moments and draw samples from them. EigenVI can also model other types of random variables (e.g., nonnegative, bounded) by constructing variational approximations from different families of orthogonal functions. Within these families, EigenVI computes the variational approximation that best matches the score function of the target distribution by minimizing a stochastic estimate of the Fisher divergence. Notably, this optimization reduces to solving a minimum eigenvalue problem, so that EigenVI effectively sidesteps the iterative gradient-based optimizations that are required for many other BBVI algorithms. (Gradient-based methods can be sensitive to learning rates, termination criteria, and other tunable hyperparameters.) We use EigenVI to approximate a variety of target distributions, including a benchmark suite of Bayesian models from posteriordb. On these distributions, we find that EigenVI is more accurate than existing methods for Gaussian BBVI.
Estimating the Causal Effects of T Cell Receptors
Oct 18, 2024



Abstract:A central question in human immunology is how a patient's repertoire of T cells impacts disease. Here, we introduce a method to infer the causal effects of T cell receptor (TCR) sequences on patient outcomes using observational TCR repertoire sequencing data and clinical outcomes data. Our approach corrects for unobserved confounders, such as a patient's environment and life history, by using the patient's immature, pre-selection TCR repertoire. The pre-selection repertoire can be estimated from nonproductive TCR data, which is widely available. It is generated by a randomized mutational process, V(D)J recombination, which provides a natural experiment. We show formally how to use the pre-selection repertoire to draw causal inferences, and develop a scalable neural-network estimator for our identification formula. Our method produces an estimate of the effect of interventions that add a specific TCR sequence to patient repertoires. As a demonstration, we use it to analyze the effects of TCRs on COVID-19 severity, uncovering potentially therapeutic TCRs that are (1) observed in patients, (2) bind SARS-CoV-2 antigens in vitro and (3) have strong positive effects on clinical outcomes.
Hypothesis Testing the Circuit Hypothesis in LLMs
Oct 16, 2024Abstract:Large language models (LLMs) demonstrate surprising capabilities, but we do not understand how they are implemented. One hypothesis suggests that these capabilities are primarily executed by small subnetworks within the LLM, known as circuits. But how can we evaluate this hypothesis? In this paper, we formalize a set of criteria that a circuit is hypothesized to meet and develop a suite of hypothesis tests to evaluate how well circuits satisfy them. The criteria focus on the extent to which the LLM's behavior is preserved, the degree of localization of this behavior, and whether the circuit is minimal. We apply these tests to six circuits described in the research literature. We find that synthetic circuits -- circuits that are hard-coded in the model -- align with the idealized properties. Circuits discovered in Transformer models satisfy the criteria to varying degrees. To facilitate future empirical studies of circuits, we created the \textit{circuitry} package, a wrapper around the \textit{TransformerLens} library, which abstracts away lower-level manipulations of hooks and activations. The software is available at \url{https://github.com/blei-lab/circuitry}.
Estimating Wage Disparities Using Foundation Models
Sep 15, 2024



Abstract:One thread of empirical work in social science focuses on decomposing group differences in outcomes into unexplained components and components explained by observable factors. In this paper, we study gender wage decompositions, which require estimating the portion of the gender wage gap explained by career histories of workers. Classical methods for decomposing the wage gap employ simple predictive models of wages which condition on a small set of simple summaries of labor history. The problem is that these predictive models cannot take advantage of the full complexity of a worker's history, and the resulting decompositions thus suffer from omitted variable bias (OVB), where covariates that are correlated with both gender and wages are not included in the model. Here we explore an alternative methodology for wage gap decomposition that employs powerful foundation models, such as large language models, as the predictive engine. Foundation models excel at making accurate predictions from complex, high-dimensional inputs. We use a custom-built foundation model, designed to predict wages from full labor histories, to decompose the gender wage gap. We prove that the way such models are usually trained might still lead to OVB, but develop fine-tuning algorithms that empirically mitigate this issue. Our model captures a richer representation of career history than simple models and predicts wages more accurately. In detail, we first provide a novel set of conditions under which an estimator of the wage gap based on a fine-tuned foundation model is $\sqrt{n}$-consistent. Building on the theory, we then propose methods for fine-tuning foundation models that minimize OVB. Using data from the Panel Study of Income Dynamics, we find that history explains more of the gender wage gap than standard econometric models can measure, and we identify elements of history that are important for reducing OVB.
Batch and match: black-box variational inference with a score-based divergence
Feb 22, 2024



Abstract:Most leading implementations of black-box variational inference (BBVI) are based on optimizing a stochastic evidence lower bound (ELBO). But such approaches to BBVI often converge slowly due to the high variance of their gradient estimates. In this work, we propose batch and match (BaM), an alternative approach to BBVI based on a score-based divergence. Notably, this score-based divergence can be optimized by a closed-form proximal update for Gaussian variational families with full covariance matrices. We analyze the convergence of BaM when the target distribution is Gaussian, and we prove that in the limit of infinite batch size the variational parameter updates converge exponentially quickly to the target mean and covariance. We also evaluate the performance of BaM on Gaussian and non-Gaussian target distributions that arise from posterior inference in hierarchical and deep generative models. In these experiments, we find that BaM typically converges in fewer (and sometimes significantly fewer) gradient evaluations than leading implementations of BBVI based on ELBO maximization.
Hierarchical Causal Models
Jan 10, 2024Abstract:Scientists often want to learn about cause and effect from hierarchical data, collected from subunits nested inside units. Consider students in schools, cells in patients, or cities in states. In such settings, unit-level variables (e.g. each school's budget) may affect subunit-level variables (e.g. the test scores of each student in each school) and vice versa. To address causal questions with hierarchical data, we propose hierarchical causal models, which extend structural causal models and causal graphical models by adding inner plates. We develop a general graphical identification technique for hierarchical causal models that extends do-calculus. We find many situations in which hierarchical data can enable causal identification even when it would be impossible with non-hierarchical data, that is, if we had only unit-level summaries of subunit-level variables (e.g. the school's average test score, rather than each student's score). We develop estimation techniques for hierarchical causal models, using methods including hierarchical Bayesian models. We illustrate our results in simulation and via a reanalysis of the classic "eight schools" study.
Revisiting Topic-Guided Language Models
Dec 04, 2023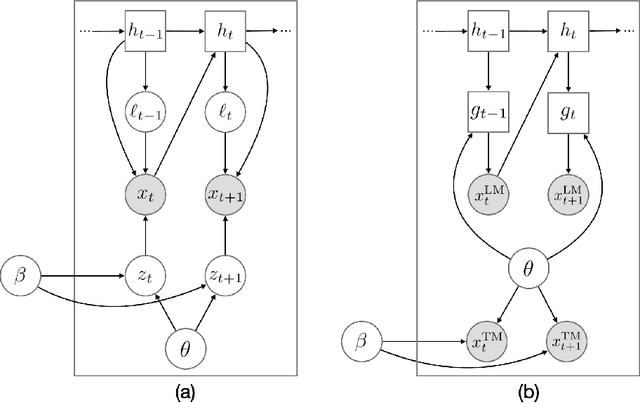
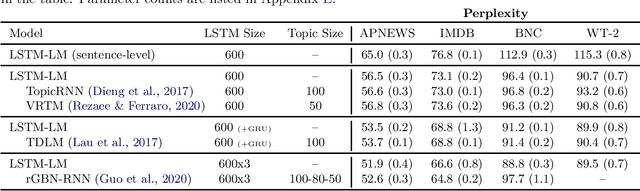

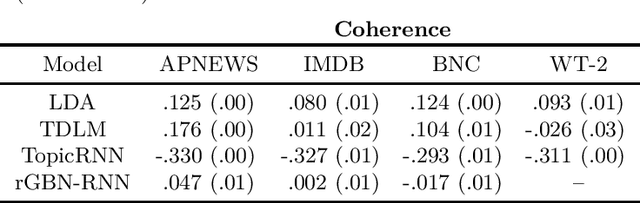
Abstract:A recent line of work in natural language processing has aimed to combine language models and topic models. These topic-guided language models augment neural language models with topic models, unsupervised learning methods that can discover document-level patterns of word use. This paper compares the effectiveness of these methods in a standardized setting. We study four topic-guided language models and two baselines, evaluating the held-out predictive performance of each model on four corpora. Surprisingly, we find that none of these methods outperform a standard LSTM language model baseline, and most fail to learn good topics. Further, we train a probe of the neural language model that shows that the baseline's hidden states already encode topic information. We make public all code used for this study.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge