EigenVI: score-based variational inference with orthogonal function expansions

We develop EigenVI, an eigenvalue-based approach for black-box variational inference (BBVI). EigenVI constructs its variational approximations from orthogonal function expansions. For distributions over $\mathbb{R}^D$, the lowest order term in these expansions provides a Gaussian variational approximation, while higher-order terms provide a systematic way to model non-Gaussianity. These approximations are flexible enough to model complex distributions (multimodal, asymmetric), but they are simple enough that one can calculate their low-order moments and draw samples from them. EigenVI can also model other types of random variables (e.g., nonnegative, bounded) by constructing variational approximations from different families of orthogonal functions. Within these families, EigenVI computes the variational approximation that best matches the score function of the target distribution by minimizing a stochastic estimate of the Fisher divergence. Notably, this optimization reduces to solving a minimum eigenvalue problem, so that EigenVI effectively sidesteps the iterative gradient-based optimizations that are required for many other BBVI algorithms. (Gradient-based methods can be sensitive to learning rates, termination criteria, and other tunable hyperparameters.) We use EigenVI to approximate a variety of target distributions, including a benchmark suite of Bayesian models from posteriordb. On these distributions, we find that EigenVI is more accurate than existing methods for Gaussian BBVI.

Variational Inference in Location-Scale Families: Exact Recovery of the Mean and Correlation Matrix

Given an intractable target density $p$, variational inference (VI) attempts to find the best approximation $q$ from a tractable family $Q$. This is typically done by minimizing the exclusive Kullback-Leibler divergence, $\text{KL}(q||p)$. In practice, $Q$ is not rich enough to contain $p$, and the approximation is misspecified even when it is a unique global minimizer of $\text{KL}(q||p)$. In this paper, we analyze the robustness of VI to these misspecifications when $p$ exhibits certain symmetries and $Q$ is a location-scale family that shares these symmetries. We prove strong guarantees for VI not only under mild regularity conditions but also in the face of severe misspecifications. Namely, we show that (i) VI recovers the mean of $p$ when $p$ exhibits an \textit{even} symmetry, and (ii) it recovers the correlation matrix of $p$ when in addition~$p$ exhibits an \textit{elliptical} symmetry. These guarantees hold for the mean even when $q$ is factorized and $p$ is not, and for the correlation matrix even when~$q$ and~$p$ behave differently in their tails. We analyze various regimes of Bayesian inference where these symmetries are useful idealizations, and we also investigate experimentally how VI behaves in their absence.

An Ordering of Divergences for Variational Inference with Factorized Gaussian Approximations

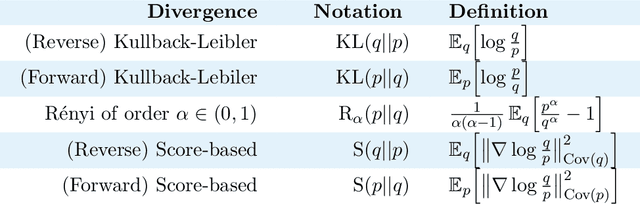
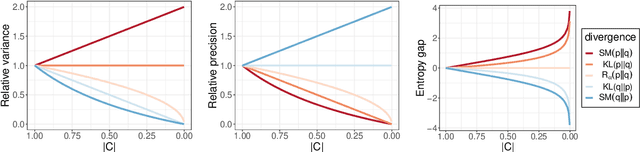
Given an intractable distribution $p$, the problem of variational inference (VI) is to compute the best approximation $q$ from some more tractable family $\mathcal{Q}$. Most commonly the approximation is found by minimizing a Kullback-Leibler (KL) divergence. However, there exist other valid choices of divergences, and when $\mathcal{Q}$ does not contain~$p$, each divergence champions a different solution. We analyze how the choice of divergence affects the outcome of VI when a Gaussian with a dense covariance matrix is approximated by a Gaussian with a diagonal covariance matrix. In this setting we show that different divergences can be \textit{ordered} by the amount that their variational approximations misestimate various measures of uncertainty, such as the variance, precision, and entropy. We also derive an impossibility theorem showing that no two of these measures can be simultaneously matched by a factorized approximation; hence, the choice of divergence informs which measure, if any, is correctly estimated. Our analysis covers the KL divergence, the R\'enyi divergences, and a score-based divergence that compares $\nabla\log p$ and $\nabla\log q$. We empirically evaluate whether these orderings hold when VI is used to approximate non-Gaussian distributions.

Listening to the Noise: Blind Denoising with Gibbs Diffusion

In recent years, denoising problems have become intertwined with the development of deep generative models. In particular, diffusion models are trained like denoisers, and the distribution they model coincide with denoising priors in the Bayesian picture. However, denoising through diffusion-based posterior sampling requires the noise level and covariance to be known, preventing blind denoising. We overcome this limitation by introducing Gibbs Diffusion (GDiff), a general methodology addressing posterior sampling of both the signal and the noise parameters. Assuming arbitrary parametric Gaussian noise, we develop a Gibbs algorithm that alternates sampling steps from a conditional diffusion model trained to map the signal prior to the family of noise distributions, and a Monte Carlo sampler to infer the noise parameters. Our theoretical analysis highlights potential pitfalls, guides diagnostic usage, and quantifies errors in the Gibbs stationary distribution caused by the diffusion model. We showcase our method for 1) blind denoising of natural images involving colored noises with unknown amplitude and spectral index, and 2) a cosmology problem, namely the analysis of cosmic microwave background data, where Bayesian inference of "noise" parameters means constraining models of the evolution of the Universe.

Batch and match: black-box variational inference with a score-based divergence

Most leading implementations of black-box variational inference (BBVI) are based on optimizing a stochastic evidence lower bound (ELBO). But such approaches to BBVI often converge slowly due to the high variance of their gradient estimates. In this work, we propose batch and match (BaM), an alternative approach to BBVI based on a score-based divergence. Notably, this score-based divergence can be optimized by a closed-form proximal update for Gaussian variational families with full covariance matrices. We analyze the convergence of BaM when the target distribution is Gaussian, and we prove that in the limit of infinite batch size the variational parameter updates converge exponentially quickly to the target mean and covariance. We also evaluate the performance of BaM on Gaussian and non-Gaussian target distributions that arise from posterior inference in hierarchical and deep generative models. In these experiments, we find that BaM typically converges in fewer (and sometimes significantly fewer) gradient evaluations than leading implementations of BBVI based on ELBO maximization.

Amortized Variational Inference: When and Why?

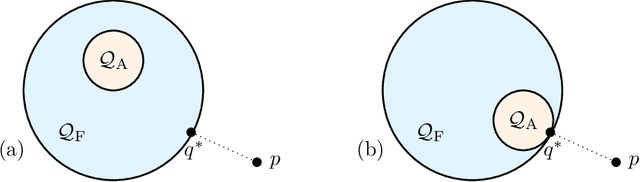
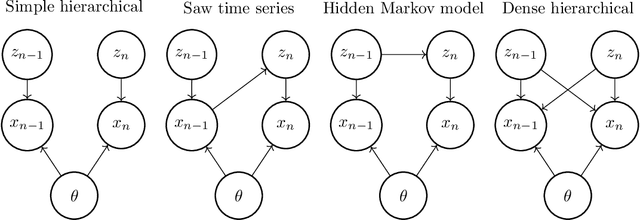
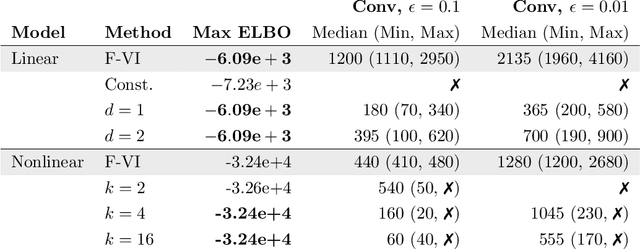
Amortized variational inference (A-VI) is a method for approximating the intractable posterior distributions that arise in probabilistic models. The defining feature of A-VI is that it learns a global inference function that maps each observation to its local latent variable's approximate posterior. This stands in contrast to the more classical factorized (or mean-field) variational inference (F-VI), which directly learns the parameters of the approximating distribution for each latent variable. In deep generative models, A-VI is used as a computational trick to speed up inference for local latent variables. In this paper, we study A-VI as a general alternative to F-VI for approximate posterior inference. A-VI cannot produce an approximation with a lower Kullback-Leibler divergence than F-VI's optimal solution, because the amortized family is a subset of the factorized family. Thus a central theoretical problem is to characterize when A-VI still attains F-VI's optimal solution. We derive conditions on both the model and the inference function under which A-VI can theoretically achieve F-VI's optimum. We show that for a broad class of hierarchical models, including deep generative models, it is possible to close the gap between A-VI and F-VI. Further, for an even broader class of models, we establish when and how to expand the domain of the inference function to make amortization a feasible strategy. Finally, we prove that for certain models -- including hidden Markov models and Gaussian processes -- A-VI cannot match F-VI's solution, no matter how expressive the inference function is. We also study A-VI empirically. On several examples, we corroborate our theoretical results and investigate the performance of A-VI when varying the complexity of the inference function. When the gap between A-VI and F-VI can be closed, we find that the required complexity of the function need not scale with the number of observations, and that A-VI often converges faster than F-VI.

The Shrinkage-Delinkage Trade-off: An Analysis of Factorized Gaussian Approximations for Variational Inference

When factorized approximations are used for variational inference (VI), they tend to understimate the uncertainty -- as measured in various ways -- of the distributions they are meant to approximate. We consider two popular ways to measure the uncertainty deficit of VI: (i) the degree to which it underestimates the componentwise variance, and (ii) the degree to which it underestimates the entropy. To better understand these effects, and the relationship between them, we examine an informative setting where they can be explicitly (and elegantly) analyzed: the approximation of a Gaussian,~$p$, with a dense covariance matrix, by a Gaussian,~$q$, with a diagonal covariance matrix. We prove that $q$ always underestimates both the componentwise variance and the entropy of $p$, \textit{though not necessarily to the same degree}. Moreover we demonstrate that the entropy of $q$ is determined by the trade-off of two competing forces: it is decreased by the shrinkage of its componentwise variances (our first measure of uncertainty) but it is increased by the factorized approximation which delinks the nodes in the graphical model of $p$. We study various manifestations of this trade-off, notably one where, as the dimension of the problem grows, the per-component entropy gap between $p$ and $q$ becomes vanishingly small even though $q$ underestimates every componentwise variance by a constant multiplicative factor. We also use the shrinkage-delinkage trade-off to bound the entropy gap in terms of the problem dimension and the condition number of the correlation matrix of $p$. Finally we present empirical results on both Gaussian and non-Gaussian targets, the former to validate our analysis and the latter to explore its limitations.