EigenVI: score-based variational inference with orthogonal function expansions

We develop EigenVI, an eigenvalue-based approach for black-box variational inference (BBVI). EigenVI constructs its variational approximations from orthogonal function expansions. For distributions over $\mathbb{R}^D$, the lowest order term in these expansions provides a Gaussian variational approximation, while higher-order terms provide a systematic way to model non-Gaussianity. These approximations are flexible enough to model complex distributions (multimodal, asymmetric), but they are simple enough that one can calculate their low-order moments and draw samples from them. EigenVI can also model other types of random variables (e.g., nonnegative, bounded) by constructing variational approximations from different families of orthogonal functions. Within these families, EigenVI computes the variational approximation that best matches the score function of the target distribution by minimizing a stochastic estimate of the Fisher divergence. Notably, this optimization reduces to solving a minimum eigenvalue problem, so that EigenVI effectively sidesteps the iterative gradient-based optimizations that are required for many other BBVI algorithms. (Gradient-based methods can be sensitive to learning rates, termination criteria, and other tunable hyperparameters.) We use EigenVI to approximate a variety of target distributions, including a benchmark suite of Bayesian models from posteriordb. On these distributions, we find that EigenVI is more accurate than existing methods for Gaussian BBVI.

Batch, match, and patch: low-rank approximations for score-based variational inference

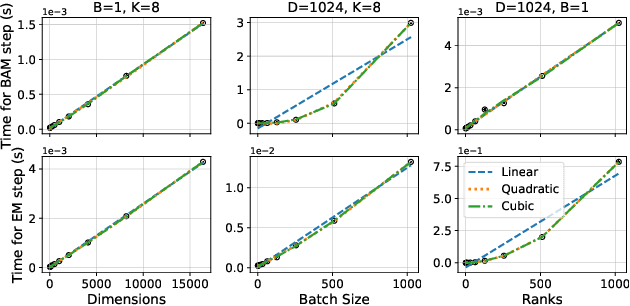
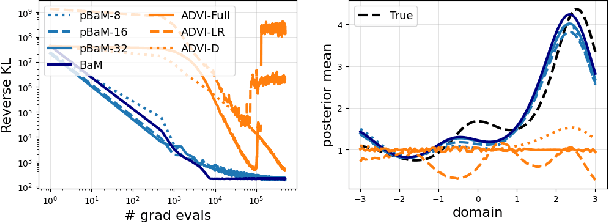
Black-box variational inference (BBVI) scales poorly to high dimensional problems when it is used to estimate a multivariate Gaussian approximation with a full covariance matrix. In this paper, we extend the batch-and-match (BaM) framework for score-based BBVI to problems where it is prohibitively expensive to store such covariance matrices, let alone to estimate them. Unlike classical algorithms for BBVI, which use gradient descent to minimize the reverse Kullback-Leibler divergence, BaM uses more specialized updates to match the scores of the target density and its Gaussian approximation. We extend the updates for BaM by integrating them with a more compact parameterization of full covariance matrices. In particular, borrowing ideas from factor analysis, we add an extra step to each iteration of BaM -- a patch -- that projects each newly updated covariance matrix into a more efficiently parameterized family of diagonal plus low rank matrices. We evaluate this approach on a variety of synthetic target distributions and real-world problems in high-dimensional inference.

Variational Inference in Location-Scale Families: Exact Recovery of the Mean and Correlation Matrix

Given an intractable target density $p$, variational inference (VI) attempts to find the best approximation $q$ from a tractable family $Q$. This is typically done by minimizing the exclusive Kullback-Leibler divergence, $\text{KL}(q||p)$. In practice, $Q$ is not rich enough to contain $p$, and the approximation is misspecified even when it is a unique global minimizer of $\text{KL}(q||p)$. In this paper, we analyze the robustness of VI to these misspecifications when $p$ exhibits certain symmetries and $Q$ is a location-scale family that shares these symmetries. We prove strong guarantees for VI not only under mild regularity conditions but also in the face of severe misspecifications. Namely, we show that (i) VI recovers the mean of $p$ when $p$ exhibits an \textit{even} symmetry, and (ii) it recovers the correlation matrix of $p$ when in addition~$p$ exhibits an \textit{elliptical} symmetry. These guarantees hold for the mean even when $q$ is factorized and $p$ is not, and for the correlation matrix even when~$q$ and~$p$ behave differently in their tails. We analyze various regimes of Bayesian inference where these symmetries are useful idealizations, and we also investigate experimentally how VI behaves in their absence.

An Ordering of Divergences for Variational Inference with Factorized Gaussian Approximations

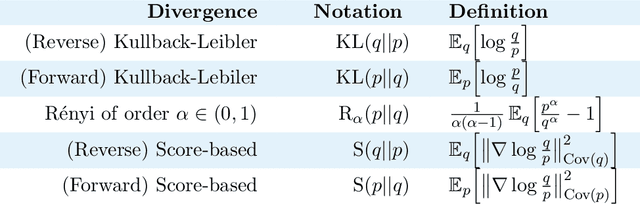
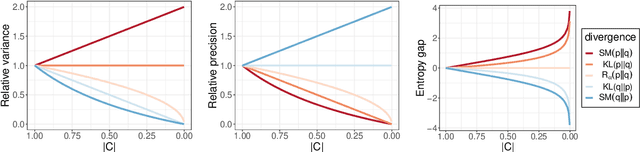
Given an intractable distribution $p$, the problem of variational inference (VI) is to compute the best approximation $q$ from some more tractable family $\mathcal{Q}$. Most commonly the approximation is found by minimizing a Kullback-Leibler (KL) divergence. However, there exist other valid choices of divergences, and when $\mathcal{Q}$ does not contain~$p$, each divergence champions a different solution. We analyze how the choice of divergence affects the outcome of VI when a Gaussian with a dense covariance matrix is approximated by a Gaussian with a diagonal covariance matrix. In this setting we show that different divergences can be \textit{ordered} by the amount that their variational approximations misestimate various measures of uncertainty, such as the variance, precision, and entropy. We also derive an impossibility theorem showing that no two of these measures can be simultaneously matched by a factorized approximation; hence, the choice of divergence informs which measure, if any, is correctly estimated. Our analysis covers the KL divergence, the R\'enyi divergences, and a score-based divergence that compares $\nabla\log p$ and $\nabla\log q$. We empirically evaluate whether these orderings hold when VI is used to approximate non-Gaussian distributions.

Batch and match: black-box variational inference with a score-based divergence

Most leading implementations of black-box variational inference (BBVI) are based on optimizing a stochastic evidence lower bound (ELBO). But such approaches to BBVI often converge slowly due to the high variance of their gradient estimates. In this work, we propose batch and match (BaM), an alternative approach to BBVI based on a score-based divergence. Notably, this score-based divergence can be optimized by a closed-form proximal update for Gaussian variational families with full covariance matrices. We analyze the convergence of BaM when the target distribution is Gaussian, and we prove that in the limit of infinite batch size the variational parameter updates converge exponentially quickly to the target mean and covariance. We also evaluate the performance of BaM on Gaussian and non-Gaussian target distributions that arise from posterior inference in hierarchical and deep generative models. In these experiments, we find that BaM typically converges in fewer (and sometimes significantly fewer) gradient evaluations than leading implementations of BBVI based on ELBO maximization.

The Shrinkage-Delinkage Trade-off: An Analysis of Factorized Gaussian Approximations for Variational Inference

When factorized approximations are used for variational inference (VI), they tend to understimate the uncertainty -- as measured in various ways -- of the distributions they are meant to approximate. We consider two popular ways to measure the uncertainty deficit of VI: (i) the degree to which it underestimates the componentwise variance, and (ii) the degree to which it underestimates the entropy. To better understand these effects, and the relationship between them, we examine an informative setting where they can be explicitly (and elegantly) analyzed: the approximation of a Gaussian,~$p$, with a dense covariance matrix, by a Gaussian,~$q$, with a diagonal covariance matrix. We prove that $q$ always underestimates both the componentwise variance and the entropy of $p$, \textit{though not necessarily to the same degree}. Moreover we demonstrate that the entropy of $q$ is determined by the trade-off of two competing forces: it is decreased by the shrinkage of its componentwise variances (our first measure of uncertainty) but it is increased by the factorized approximation which delinks the nodes in the graphical model of $p$. We study various manifestations of this trade-off, notably one where, as the dimension of the problem grows, the per-component entropy gap between $p$ and $q$ becomes vanishingly small even though $q$ underestimates every componentwise variance by a constant multiplicative factor. We also use the shrinkage-delinkage trade-off to bound the entropy gap in terms of the problem dimension and the condition number of the correlation matrix of $p$. Finally we present empirical results on both Gaussian and non-Gaussian targets, the former to validate our analysis and the latter to explore its limitations.

Topic Modeling of Hierarchical Corpora

We study the problem of topic modeling in corpora whose documents are organized in a multi-level hierarchy. We explore a parametric approach to this problem, assuming that the number of topics is known or can be estimated by cross-validation. The models we consider can be viewed as special (finite-dimensional) instances of hierarchical Dirichlet processes (HDPs). For these models we show that there exists a simple variational approximation for probabilistic inference. The approximation relies on a previously unexploited inequality that handles the conditional dependence between Dirichlet latent variables in adjacent levels of the model's hierarchy. We compare our approach to existing implementations of nonparametric HDPs. On several benchmarks we find that our approach is faster than Gibbs sampling and able to learn more predictive models than existing variational methods. Finally, we demonstrate the large-scale viability of our approach on two newly available corpora from researchers in computer security---one with 350,000 documents and over 6,000 internal subcategories, the other with a five-level deep hierarchy.

Nonnegative Matrix Factorization for Semi-supervised Dimensionality Reduction

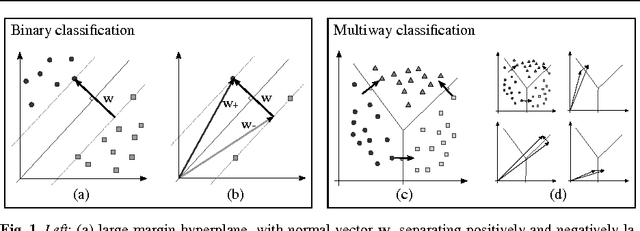
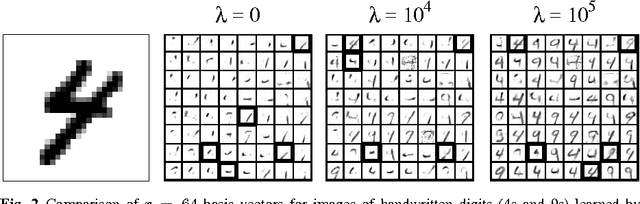
We show how to incorporate information from labeled examples into nonnegative matrix factorization (NMF), a popular unsupervised learning algorithm for dimensionality reduction. In addition to mapping the data into a space of lower dimensionality, our approach aims to preserve the nonnegative components of the data that are important for classification. We identify these components from the support vectors of large-margin classifiers and derive iterative updates to preserve them in a semi-supervised version of NMF. These updates have a simple multiplicative form like their unsupervised counterparts; they are also guaranteed at each iteration to decrease their loss function---a weighted sum of I-divergences that captures the trade-off between unsupervised and supervised learning. We evaluate these updates for dimensionality reduction when they are used as a precursor to linear classification. In this role, we find that they yield much better performance than their unsupervised counterparts. We also find one unexpected benefit of the low dimensional representations discovered by our approach: often they yield more accurate classifiers than both ordinary and transductive SVMs trained in the original input space.

Analysis and Extension of Arc-Cosine Kernels for Large Margin Classification

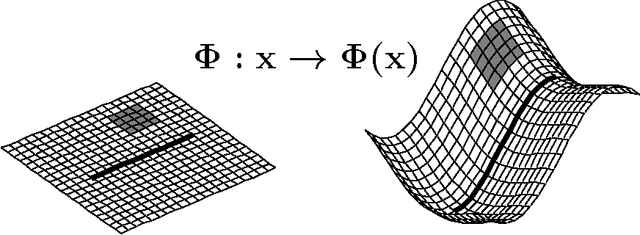
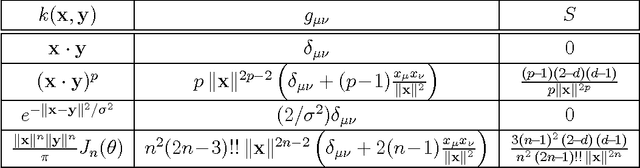
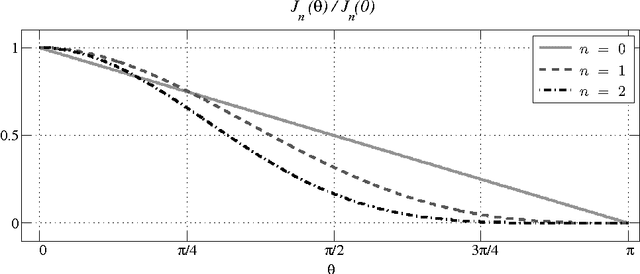
We investigate a recently proposed family of positive-definite kernels that mimic the computation in large neural networks. We examine the properties of these kernels using tools from differential geometry; specifically, we analyze the geometry of surfaces in Hilbert space that are induced by these kernels. When this geometry is described by a Riemannian manifold, we derive results for the metric, curvature, and volume element. Interestingly, though, we find that the simplest kernel in this family does not admit such an interpretation. We explore two variations of these kernels that mimic computation in neural networks with different activation functions. We experiment with these new kernels on several data sets and highlight their general trends in performance for classification.