Nonnegative Matrix Factorization for Semi-supervised Dimensionality Reduction
Paper and Code
Dec 16, 2011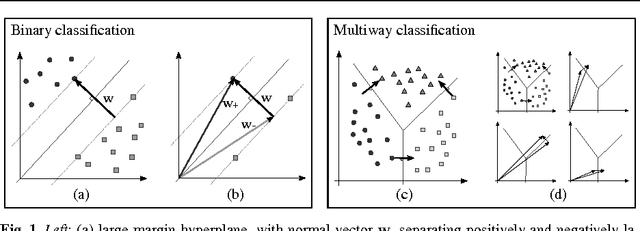

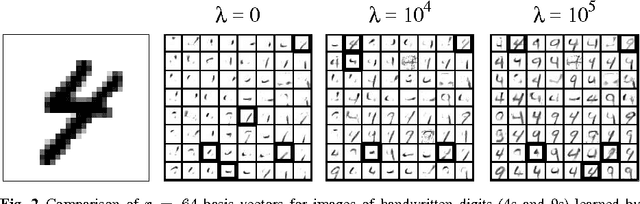

We show how to incorporate information from labeled examples into nonnegative matrix factorization (NMF), a popular unsupervised learning algorithm for dimensionality reduction. In addition to mapping the data into a space of lower dimensionality, our approach aims to preserve the nonnegative components of the data that are important for classification. We identify these components from the support vectors of large-margin classifiers and derive iterative updates to preserve them in a semi-supervised version of NMF. These updates have a simple multiplicative form like their unsupervised counterparts; they are also guaranteed at each iteration to decrease their loss function---a weighted sum of I-divergences that captures the trade-off between unsupervised and supervised learning. We evaluate these updates for dimensionality reduction when they are used as a precursor to linear classification. In this role, we find that they yield much better performance than their unsupervised counterparts. We also find one unexpected benefit of the low dimensional representations discovered by our approach: often they yield more accurate classifiers than both ordinary and transductive SVMs trained in the original input space.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge