EigenVI: score-based variational inference with orthogonal function expansions

We develop EigenVI, an eigenvalue-based approach for black-box variational inference (BBVI). EigenVI constructs its variational approximations from orthogonal function expansions. For distributions over $\mathbb{R}^D$, the lowest order term in these expansions provides a Gaussian variational approximation, while higher-order terms provide a systematic way to model non-Gaussianity. These approximations are flexible enough to model complex distributions (multimodal, asymmetric), but they are simple enough that one can calculate their low-order moments and draw samples from them. EigenVI can also model other types of random variables (e.g., nonnegative, bounded) by constructing variational approximations from different families of orthogonal functions. Within these families, EigenVI computes the variational approximation that best matches the score function of the target distribution by minimizing a stochastic estimate of the Fisher divergence. Notably, this optimization reduces to solving a minimum eigenvalue problem, so that EigenVI effectively sidesteps the iterative gradient-based optimizations that are required for many other BBVI algorithms. (Gradient-based methods can be sensitive to learning rates, termination criteria, and other tunable hyperparameters.) We use EigenVI to approximate a variety of target distributions, including a benchmark suite of Bayesian models from posteriordb. On these distributions, we find that EigenVI is more accurate than existing methods for Gaussian BBVI.

Batch, match, and patch: low-rank approximations for score-based variational inference

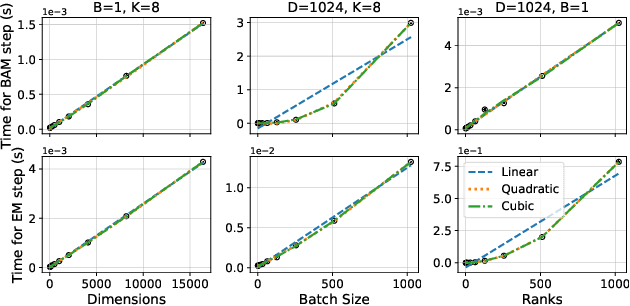
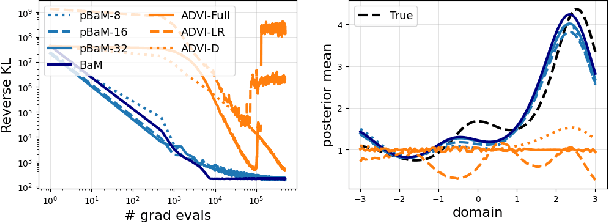
Black-box variational inference (BBVI) scales poorly to high dimensional problems when it is used to estimate a multivariate Gaussian approximation with a full covariance matrix. In this paper, we extend the batch-and-match (BaM) framework for score-based BBVI to problems where it is prohibitively expensive to store such covariance matrices, let alone to estimate them. Unlike classical algorithms for BBVI, which use gradient descent to minimize the reverse Kullback-Leibler divergence, BaM uses more specialized updates to match the scores of the target density and its Gaussian approximation. We extend the updates for BaM by integrating them with a more compact parameterization of full covariance matrices. In particular, borrowing ideas from factor analysis, we add an extra step to each iteration of BaM -- a patch -- that projects each newly updated covariance matrix into a more efficiently parameterized family of diagonal plus low rank matrices. We evaluate this approach on a variety of synthetic target distributions and real-world problems in high-dimensional inference.

ATLAS: Adapting Trajectory Lengths and Step-Size for Hamiltonian Monte Carlo

Hamiltonian Monte-Carlo (HMC) and its auto-tuned variant, the No U-Turn Sampler (NUTS) can struggle to accurately sample distributions with complex geometries, e.g., varying curvature, due to their constant step size for leapfrog integration and fixed mass matrix. In this work, we develop a strategy to locally adapt the step size parameter of HMC at every iteration by evaluating a low-rank approximation of the local Hessian and estimating its largest eigenvalue. We combine it with a strategy to similarly adapt the trajectory length by monitoring the no U-turn condition, resulting in an adaptive sampler, ATLAS: adapting trajectory length and step-size. We further use a delayed rejection framework for making multiple proposals that improves the computational efficiency of ATLAS, and develop an approach for automatically tuning its hyperparameters during warmup. We compare ATLAS with state-of-the-art samplers like NUTS on a suite of synthetic and real world examples, and show that i) unlike NUTS, ATLAS is able to accurately sample difficult distributions with complex geometries, ii) it is computationally competitive to NUTS for simpler distributions, and iii) it is more robust to the tuning of hyperparamters.

CHARM: Creating Halos with Auto-Regressive Multi-stage networks

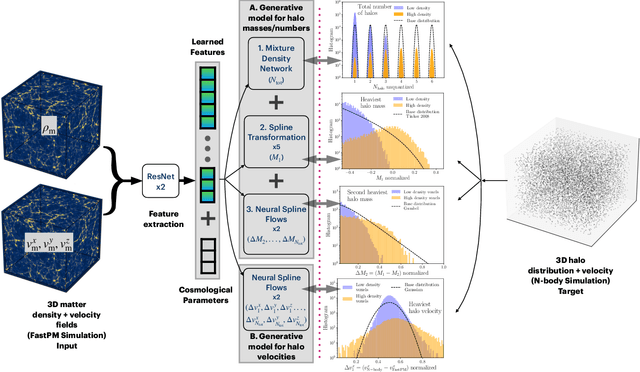
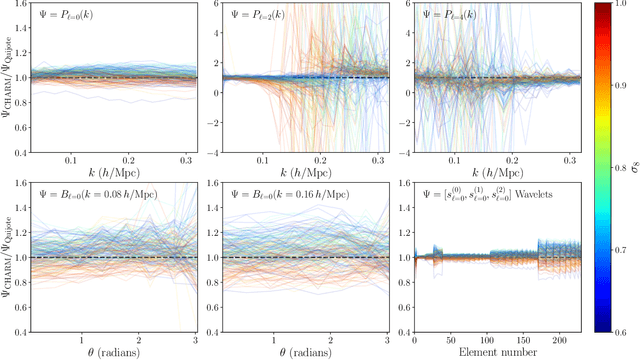
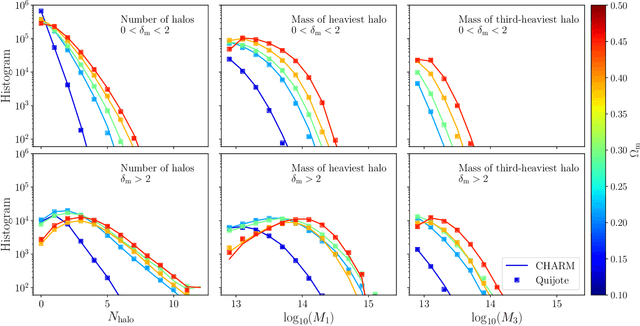
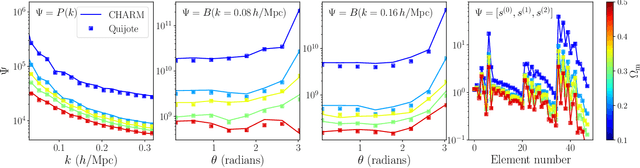
To maximize the amount of information extracted from cosmological datasets, simulations that accurately represent these observations are necessary. However, traditional simulations that evolve particles under gravity by estimating particle-particle interactions (N-body simulations) are computationally expensive and prohibitive to scale to the large volumes and resolutions necessary for the upcoming datasets. Moreover, modeling the distribution of galaxies typically involves identifying virialized dark matter halos, which is also a time- and memory-consuming process for large N-body simulations, further exacerbating the computational cost. In this study, we introduce CHARM, a novel method for creating mock halo catalogs by matching the spatial, mass, and velocity statistics of halos directly from the large-scale distribution of the dark matter density field. We develop multi-stage neural spline flow-based networks to learn this mapping at redshift z=0.5 directly with computationally cheaper low-resolution particle mesh simulations instead of relying on the high-resolution N-body simulations. We show that the mock halo catalogs and painted galaxy catalogs have the same statistical properties as obtained from $N$-body simulations in both real space and redshift space. Finally, we use these mock catalogs for cosmological inference using redshift-space galaxy power spectrum, bispectrum, and wavelet-based statistics using simulation-based inference, performing the first inference with accelerated forward model simulations and finding unbiased cosmological constraints with well-calibrated posteriors. The code was developed as part of the Simons Collaboration on Learning the Universe and is publicly available at \url{https://github.com/shivampcosmo/CHARM}.

Batch and match: black-box variational inference with a score-based divergence

Most leading implementations of black-box variational inference (BBVI) are based on optimizing a stochastic evidence lower bound (ELBO). But such approaches to BBVI often converge slowly due to the high variance of their gradient estimates. In this work, we propose batch and match (BaM), an alternative approach to BBVI based on a score-based divergence. Notably, this score-based divergence can be optimized by a closed-form proximal update for Gaussian variational families with full covariance matrices. We analyze the convergence of BaM when the target distribution is Gaussian, and we prove that in the limit of infinite batch size the variational parameter updates converge exponentially quickly to the target mean and covariance. We also evaluate the performance of BaM on Gaussian and non-Gaussian target distributions that arise from posterior inference in hierarchical and deep generative models. In these experiments, we find that BaM typically converges in fewer (and sometimes significantly fewer) gradient evaluations than leading implementations of BBVI based on ELBO maximization.

LtU-ILI: An All-in-One Framework for Implicit Inference in Astrophysics and Cosmology

This paper presents the Learning the Universe Implicit Likelihood Inference (LtU-ILI) pipeline, a codebase for rapid, user-friendly, and cutting-edge machine learning (ML) inference in astrophysics and cosmology. The pipeline includes software for implementing various neural architectures, training schema, priors, and density estimators in a manner easily adaptable to any research workflow. It includes comprehensive validation metrics to assess posterior estimate coverage, enhancing the reliability of inferred results. Additionally, the pipeline is easily parallelizable, designed for efficient exploration of modeling hyperparameters. To demonstrate its capabilities, we present real applications across a range of astrophysics and cosmology problems, such as: estimating galaxy cluster masses from X-ray photometry; inferring cosmology from matter power spectra and halo point clouds; characterising progenitors in gravitational wave signals; capturing physical dust parameters from galaxy colors and luminosities; and establishing properties of semi-analytic models of galaxy formation. We also include exhaustive benchmarking and comparisons of all implemented methods as well as discussions about the challenges and pitfalls of ML inference in astronomical sciences. All code and examples are made publicly available at https://github.com/maho3/ltu-ili.

SimBIG: Field-level Simulation-Based Inference of Galaxy Clustering

We present the first simulation-based inference (SBI) of cosmological parameters from field-level analysis of galaxy clustering. Standard galaxy clustering analyses rely on analyzing summary statistics, such as the power spectrum, $P_\ell$, with analytic models based on perturbation theory. Consequently, they do not fully exploit the non-linear and non-Gaussian features of the galaxy distribution. To address these limitations, we use the {\sc SimBIG} forward modelling framework to perform SBI using normalizing flows. We apply SimBIG to a subset of the BOSS CMASS galaxy sample using a convolutional neural network with stochastic weight averaging to perform massive data compression of the galaxy field. We infer constraints on $\Omega_m = 0.267^{+0.033}_{-0.029}$ and $\sigma_8=0.762^{+0.036}_{-0.035}$. While our constraints on $\Omega_m$ are in-line with standard $P_\ell$ analyses, those on $\sigma_8$ are $2.65\times$ tighter. Our analysis also provides constraints on the Hubble constant $H_0=64.5 \pm 3.8 \ {\rm km / s / Mpc}$ from galaxy clustering alone. This higher constraining power comes from additional non-Gaussian cosmological information, inaccessible with $P_\ell$. We demonstrate the robustness of our analysis by showcasing our ability to infer unbiased cosmological constraints from a series of test simulations that are constructed using different forward models than the one used in our training dataset. This work not only presents competitive cosmological constraints but also introduces novel methods for leveraging additional cosmological information in upcoming galaxy surveys like DESI, PFS, and Euclid.

Variational Inference with Gaussian Score Matching

Variational inference (VI) is a method to approximate the computationally intractable posterior distributions that arise in Bayesian statistics. Typically, VI fits a simple parametric distribution to the target posterior by minimizing an appropriate objective such as the evidence lower bound (ELBO). In this work, we present a new approach to VI based on the principle of score matching, that if two distributions are equal then their score functions (i.e., gradients of the log density) are equal at every point on their support. With this, we develop score matching VI, an iterative algorithm that seeks to match the scores between the variational approximation and the exact posterior. At each iteration, score matching VI solves an inner optimization, one that minimally adjusts the current variational estimate to match the scores at a newly sampled value of the latent variables. We show that when the variational family is a Gaussian, this inner optimization enjoys a closed form solution, which we call Gaussian score matching VI (GSM-VI). GSM-VI is also a ``black box'' variational algorithm in that it only requires a differentiable joint distribution, and as such it can be applied to a wide class of models. We compare GSM-VI to black box variational inference (BBVI), which has similar requirements but instead optimizes the ELBO. We study how GSM-VI behaves as a function of the problem dimensionality, the condition number of the target covariance matrix (when the target is Gaussian), and the degree of mismatch between the approximating and exact posterior distribution. We also study GSM-VI on a collection of real-world Bayesian inference problems from the posteriorDB database of datasets and models. In all of our studies we find that GSM-VI is faster than BBVI, but without sacrificing accuracy. It requires 10-100x fewer gradient evaluations to obtain a comparable quality of approximation.

Reconstructing the Universe with Variational self-Boosted Sampling

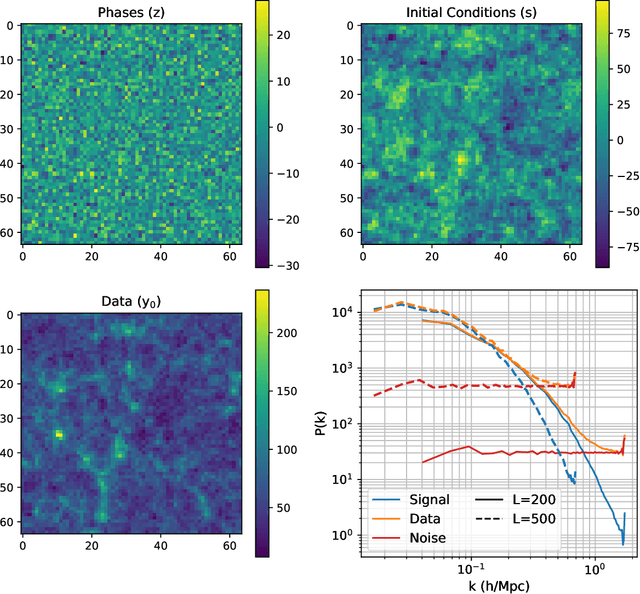
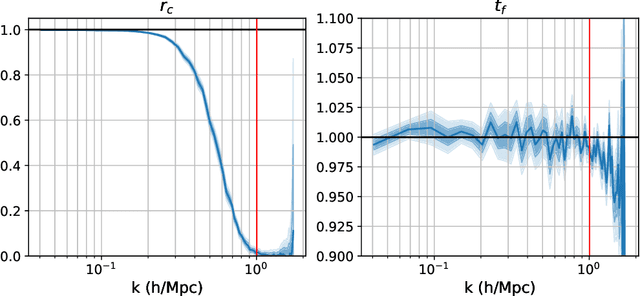
Forward modeling approaches in cosmology have made it possible to reconstruct the initial conditions at the beginning of the Universe from the observed survey data. However the high dimensionality of the parameter space still poses a challenge to explore the full posterior, with traditional algorithms such as Hamiltonian Monte Carlo (HMC) being computationally inefficient due to generating correlated samples and the performance of variational inference being highly dependent on the choice of divergence (loss) function. Here we develop a hybrid scheme, called variational self-boosted sampling (VBS) to mitigate the drawbacks of both these algorithms by learning a variational approximation for the proposal distribution of Monte Carlo sampling and combine it with HMC. The variational distribution is parameterized as a normalizing flow and learnt with samples generated on the fly, while proposals drawn from it reduce auto-correlation length in MCMC chains. Our normalizing flow uses Fourier space convolutions and element-wise operations to scale to high dimensions. We show that after a short initial warm-up and training phase, VBS generates better quality of samples than simple VI approaches and reduces the correlation length in the sampling phase by a factor of 10-50 over using only HMC to explore the posterior of initial conditions in 64$^3$ and 128$^3$ dimensional problems, with larger gains for high signal-to-noise data observations.

Delayed rejection Hamiltonian Monte Carlo for sampling multiscale distributions

The efficiency of Hamiltonian Monte Carlo (HMC) can suffer when sampling a distribution with a wide range of length scales, because the small step sizes needed for stability in high-curvature regions are inefficient elsewhere. To address this we present a delayed rejection variant: if an initial HMC trajectory is rejected, we make one or more subsequent proposals each using a step size geometrically smaller than the last. We extend the standard delayed rejection framework by allowing the probability of a retry to depend on the probability of accepting the previous proposal. We test the scheme in several sampling tasks, including multiscale model distributions such as Neal's funnel, and statistical applications. Delayed rejection enables up to five-fold performance gains over optimally-tuned HMC, as measured by effective sample size per gradient evaluation. Even for simpler distributions, delayed rejection provides increased robustness to step size misspecification. Along the way, we provide an accessible but rigorous review of detailed balance for HMC.