The optical and infrared are connected

Galaxies are often modelled as composites of separable components with distinct spectral signatures, implying that different wavelength ranges are only weakly correlated. They are not. We present a data-driven model which exploits subtle correlations between physical processes to accurately predict infrared (IR) WISE photometry from a neural summary of optical SDSS spectra. The model achieves accuracies of $\chi^2_N \approx 1$ for all photometric bands in WISE, as well as good colors. We are also able to tightly constrain typically IR-derived properties, e.g. the bolometric luminosities of AGN and dust parameters such as $\mathrm{q_{PAH}}$. We find that current SED-fitting methods are incapable of making comparable predictions, and that model misspecification often leads to correlated biases in star-formation rates and AGN luminosities. To help improve SED models, we determine what features of the optical spectrum are responsible for our improved predictions, and identify several lines (CaII, SrII, FeI, [OII] and H$\alpha$), which point to the complex chronology of star formation and chemical enrichment being incorrectly modelled.

Exposing Disparities in Flood Adaptation for Equitable Future Interventions

As governments race to implement new climate adaptation policies that prepare for more frequent flooding, they must seek policies that are effective for all communities and uphold climate justice. This requires evaluating policies not only on their overall effectiveness but also on whether their benefits are felt across all communities. We illustrate the importance of considering such disparities for flood adaptation using the FEMA National Flood Insurance Program Community Rating System and its dataset of $\sim$2.5 million flood insurance claims. We use ${\rm C{\scriptsize AUSAL}F{\scriptsize LOW}}$, a causal inference method based on deep generative models, to estimate the treatment effect of flood adaptation interventions based on a community's income, diversity, population, flood risk, educational attainment, and precipitation. We find that the program saves communities \$5,000--15,000 per household. However, these savings are not evenly spread across communities. For example, for low-income communities savings sharply decline as flood-risk increases in contrast to their high-income counterparts with all else equal. Even among low-income communities, there is a gap in savings between predominantly white and non-white communities: savings of predominantly white communities can be higher by more than \$6000 per household. As communities worldwide ramp up efforts to reduce losses inflicted by floods, simply prescribing a series flood adaptation measures is not enough. Programs must provide communities with the necessary technical and economic support to compensate for historical patterns of disenfranchisement, racism, and inequality. Future flood adaptation efforts should go beyond reducing losses overall and aim to close existing gaps to equitably support communities in the race for climate adaptation.

SimBIG: Field-level Simulation-Based Inference of Galaxy Clustering

We present the first simulation-based inference (SBI) of cosmological parameters from field-level analysis of galaxy clustering. Standard galaxy clustering analyses rely on analyzing summary statistics, such as the power spectrum, $P_\ell$, with analytic models based on perturbation theory. Consequently, they do not fully exploit the non-linear and non-Gaussian features of the galaxy distribution. To address these limitations, we use the {\sc SimBIG} forward modelling framework to perform SBI using normalizing flows. We apply SimBIG to a subset of the BOSS CMASS galaxy sample using a convolutional neural network with stochastic weight averaging to perform massive data compression of the galaxy field. We infer constraints on $\Omega_m = 0.267^{+0.033}_{-0.029}$ and $\sigma_8=0.762^{+0.036}_{-0.035}$. While our constraints on $\Omega_m$ are in-line with standard $P_\ell$ analyses, those on $\sigma_8$ are $2.65\times$ tighter. Our analysis also provides constraints on the Hubble constant $H_0=64.5 \pm 3.8 \ {\rm km / s / Mpc}$ from galaxy clustering alone. This higher constraining power comes from additional non-Gaussian cosmological information, inaccessible with $P_\ell$. We demonstrate the robustness of our analysis by showcasing our ability to infer unbiased cosmological constraints from a series of test simulations that are constructed using different forward models than the one used in our training dataset. This work not only presents competitive cosmological constraints but also introduces novel methods for leveraging additional cosmological information in upcoming galaxy surveys like DESI, PFS, and Euclid.

Robust Simulation-Based Inference in Cosmology with Bayesian Neural Networks

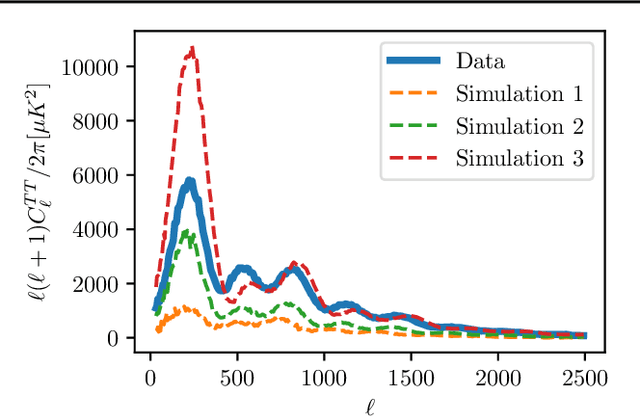
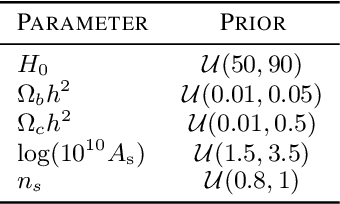
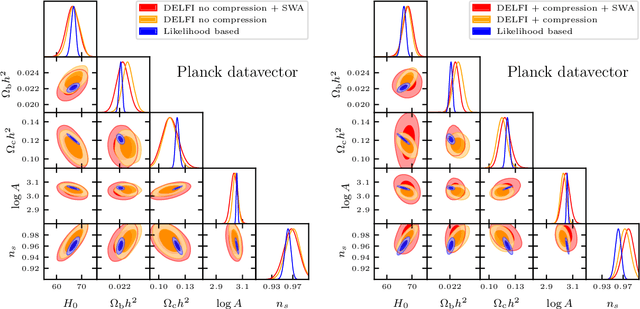
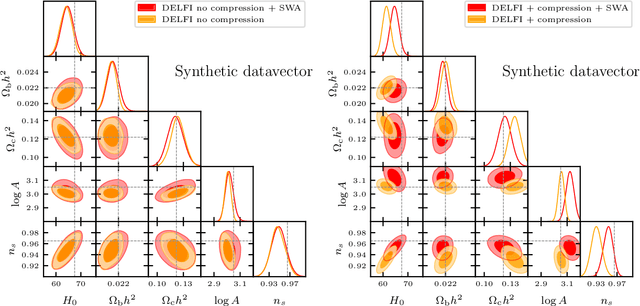
Simulation-based inference (SBI) is rapidly establishing itself as a standard machine learning technique for analyzing data in cosmological surveys. Despite continual improvements to the quality of density estimation by learned models, applications of such techniques to real data are entirely reliant on the generalization power of neural networks far outside the training distribution, which is mostly unconstrained. Due to the imperfections in scientist-created simulations, and the large computational expense of generating all possible parameter combinations, SBI methods in cosmology are vulnerable to such generalization issues. Here, we discuss the effects of both issues, and show how using a Bayesian neural network framework for training SBI can mitigate biases, and result in more reliable inference outside the training set. We introduce cosmoSWAG, the first application of Stochastic Weight Averaging to cosmology, and apply it to SBI trained for inference on the cosmic microwave background.

Accelerated Bayesian SED Modeling using Amortized Neural Posterior Estimation

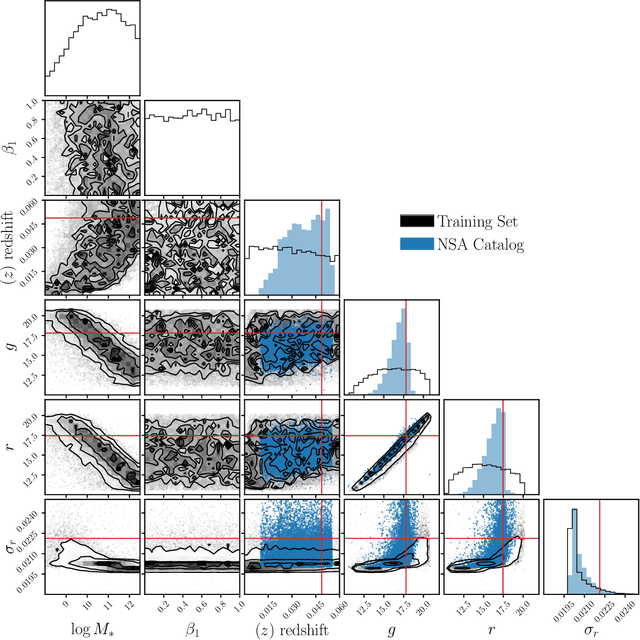
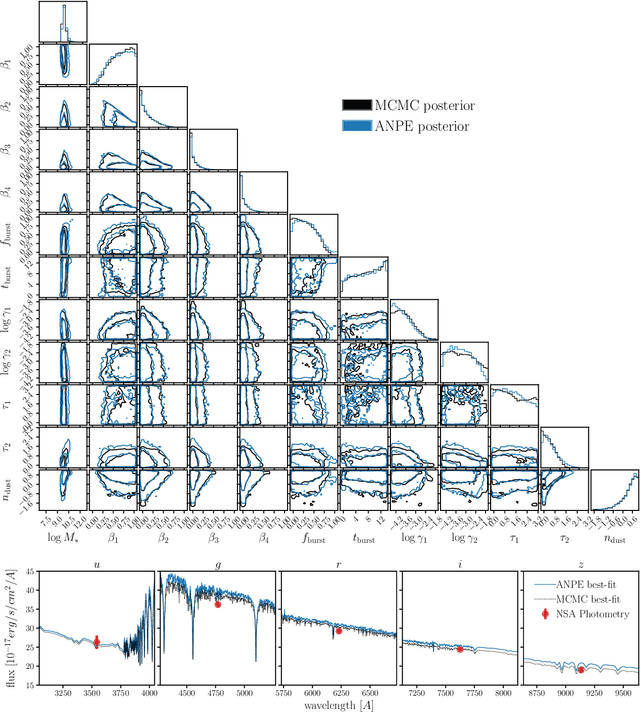
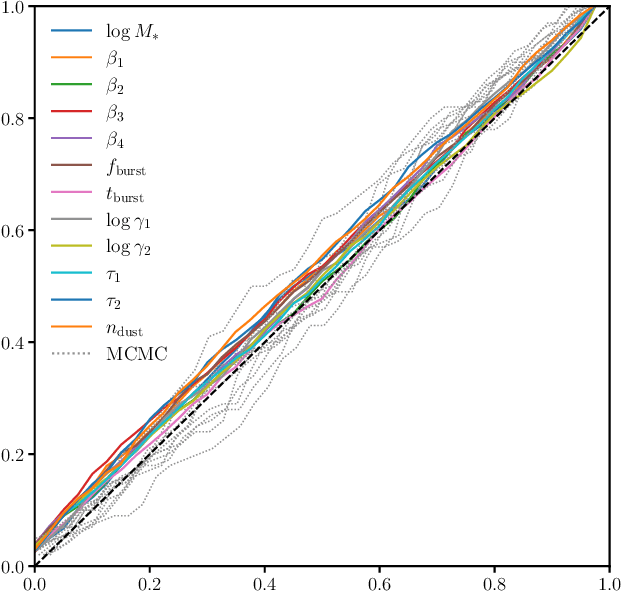
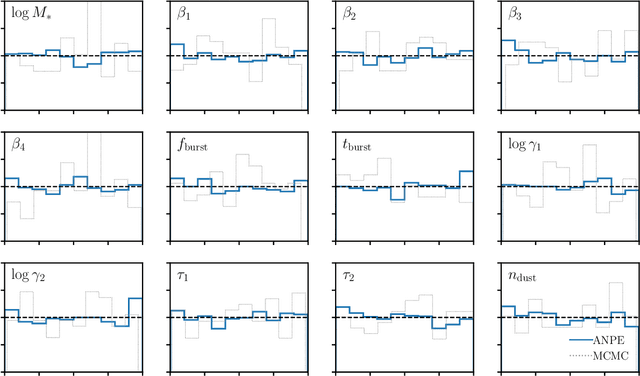
State-of-the-art spectral energy distribution (SED) analyses use a Bayesian framework to infer the physical properties of galaxies from observed photometry or spectra. They require sampling from a high-dimensional space of SED model parameters and take $>10-100$ CPU hours per galaxy, which renders them practically infeasible for analyzing the $billions$ of galaxies that will be observed by upcoming galaxy surveys ($e.g.$ DESI, PFS, Rubin, Webb, and Roman). In this work, we present an alternative scalable approach to rigorous Bayesian inference using Amortized Neural Posterior Estimation (ANPE). ANPE is a simulation-based inference method that employs neural networks to estimate the posterior probability distribution over the full range of observations. Once trained, it requires no additional model evaluations to estimate the posterior. We present, and publicly release, ${\rm SED}{flow}$, an ANPE method to produce posteriors of the recent Hahn et al. (2022) SED model from optical photometry. ${\rm SED}{flow}$ takes ${\sim}1$ $second~per~galaxy$ to obtain the posterior distributions of 12 model parameters, all of which are in excellent agreement with traditional Markov Chain Monte Carlo sampling results. We also apply ${\rm SED}{flow}$ to 33,884 galaxies in the NASA-Sloan Atlas and publicly release their posteriors: see https://changhoonhahn.github.io/SEDflow.

The CAMELS project: public data release

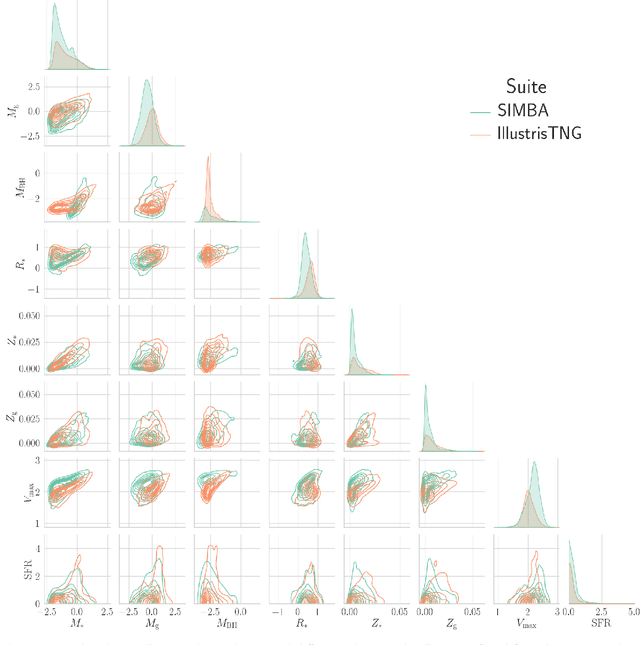
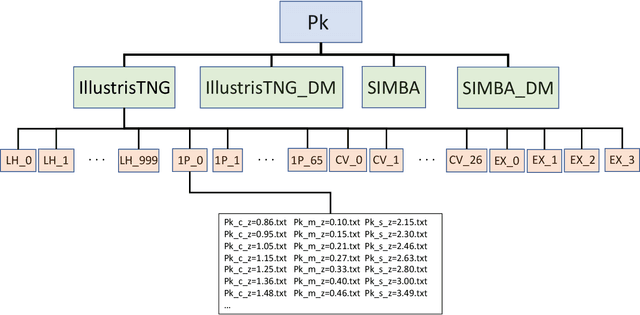
The Cosmology and Astrophysics with MachinE Learning Simulations (CAMELS) project was developed to combine cosmology with astrophysics through thousands of cosmological hydrodynamic simulations and machine learning. CAMELS contains 4,233 cosmological simulations, 2,049 N-body and 2,184 state-of-the-art hydrodynamic simulations that sample a vast volume in parameter space. In this paper we present the CAMELS public data release, describing the characteristics of the CAMELS simulations and a variety of data products generated from them, including halo, subhalo, galaxy, and void catalogues, power spectra, bispectra, Lyman-$\alpha$ spectra, probability distribution functions, halo radial profiles, and X-rays photon lists. We also release over one thousand catalogues that contain billions of galaxies from CAMELS-SAM: a large collection of N-body simulations that have been combined with the Santa Cruz Semi-Analytic Model. We release all the data, comprising more than 350 terabytes and containing 143,922 snapshots, millions of halos, galaxies and summary statistics. We provide further technical details on how to access, download, read, and process the data at \url{https://camels.readthedocs.io}.

Learning neutrino effects in Cosmology with Convolutional Neural Networks

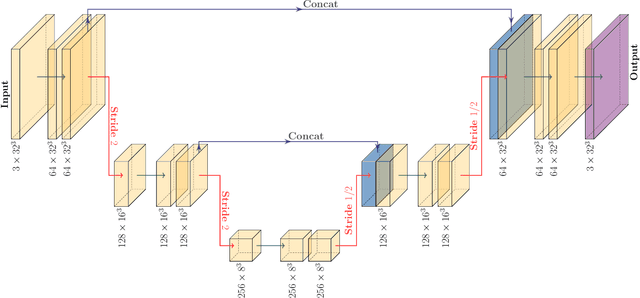
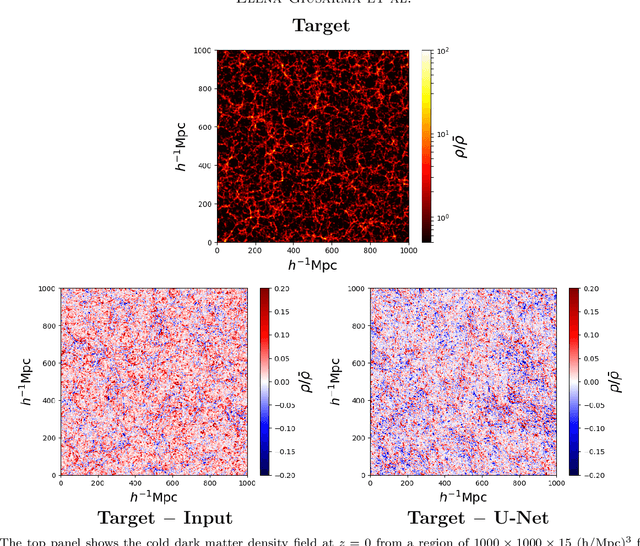
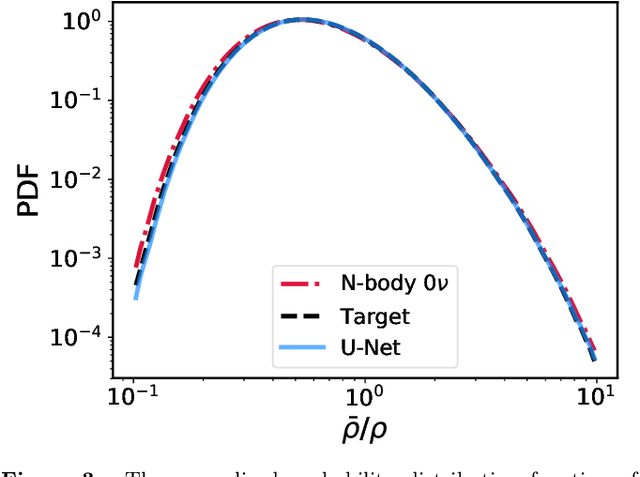
Measuring the sum of the three active neutrino masses, $M_\nu$, is one of the most important challenges in modern cosmology. Massive neutrinos imprint characteristic signatures on several cosmological observables in particular on the large-scale structure of the Universe. In order to maximize the information that can be retrieved from galaxy surveys, accurate theoretical predictions in the non-linear regime are needed. Currently, one way to achieve those predictions is by running cosmological numerical simulations. Unfortunately, producing those simulations requires high computational resources -- seven hundred CPU hours for each neutrino mass case. In this work, we propose a new method, based on a deep learning network (U-Net), to quickly generate simulations with massive neutrinos from standard $\Lambda$CDM simulations without neutrinos. We computed multiple relevant statistical measures of deep-learning generated simulations, and conclude that our method accurately reproduces the 3-dimensional spatial distribution of matter down to non-linear scales: $k < 0.7$ h/Mpc. Finally, our method allows us to generate massive neutrino simulations 10,000 times faster than the traditional methods.