Field-level simulation-based inference with galaxy catalogs: the impact of systematic effects

It has been recently shown that a powerful way to constrain cosmological parameters from galaxy redshift surveys is to train graph neural networks to perform field-level likelihood-free inference without imposing cuts on scale. In particular, de Santi et al. (2023) developed models that could accurately infer the value of $\Omega_{\rm m}$ from catalogs that only contain the positions and radial velocities of galaxies that are robust to uncertainties in astrophysics and subgrid models. However, observations are affected by many effects, including 1) masking, 2) uncertainties in peculiar velocities and radial distances, and 3) different galaxy selections. Moreover, observations only allow us to measure redshift, intertwining galaxies' radial positions and velocities. In this paper we train and test our models on galaxy catalogs, created from thousands of state-of-the-art hydrodynamic simulations run with different codes from the CAMELS project, that incorporate these observational effects. We find that, although the presence of these effects degrades the precision and accuracy of the models, and increases the fraction of catalogs where the model breaks down, the fraction of galaxy catalogs where the model performs well is over 90 %, demonstrating the potential of these models to constrain cosmological parameters even when applied to real data.

The SZ flux-mass relation at low halo masses: improvements with symbolic regression and strong constraints on baryonic feedback

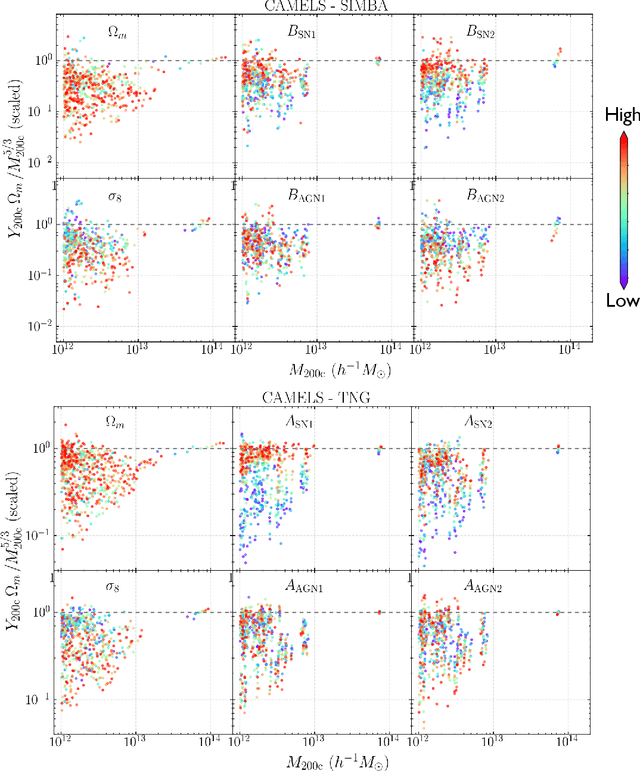
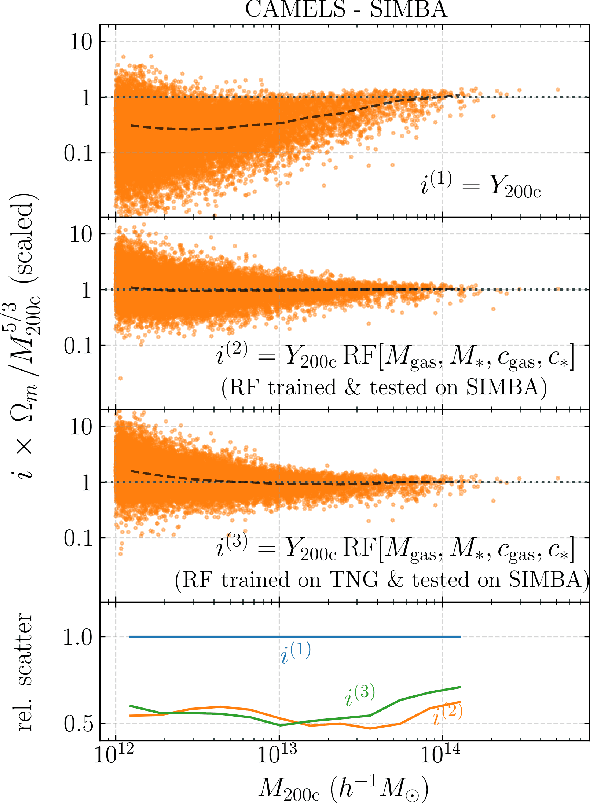
Ionized gas in the halo circumgalactic medium leaves an imprint on the cosmic microwave background via the thermal Sunyaev-Zeldovich (tSZ) effect. Feedback from active galactic nuclei (AGN) and supernovae can affect the measurements of the integrated tSZ flux of halos ($Y_\mathrm{SZ}$) and cause its relation with the halo mass ($Y_\mathrm{SZ}-M$) to deviate from the self-similar power-law prediction of the virial theorem. We perform a comprehensive study of such deviations using CAMELS, a suite of hydrodynamic simulations with extensive variations in feedback prescriptions. We use a combination of two machine learning tools (random forest and symbolic regression) to search for analogues of the $Y-M$ relation which are more robust to feedback processes for low masses ($M\lesssim 10^{14}\, h^{-1} \, M_\odot$); we find that simply replacing $Y\rightarrow Y(1+M_*/M_\mathrm{gas})$ in the relation makes it remarkably self-similar. This could serve as a robust multiwavelength mass proxy for low-mass clusters and galaxy groups. Our methodology can also be generally useful to improve the domain of validity of other astrophysical scaling relations. We also forecast that measurements of the $Y-M$ relation could provide percent-level constraints on certain combinations of feedback parameters and/or rule out a major part of the parameter space of supernova and AGN feedback models used in current state-of-the-art hydrodynamic simulations. Our results can be useful for using upcoming SZ surveys (e.g. SO, CMB-S4) and galaxy surveys (e.g. DESI and Rubin) to constrain the nature of baryonic feedback. Finally, we find that the an alternative relation, $Y-M_*$, provides complementary information on feedback than $Y-M$.

Simple lessons from complex learning: what a neural network model learns about cosmic structure formation

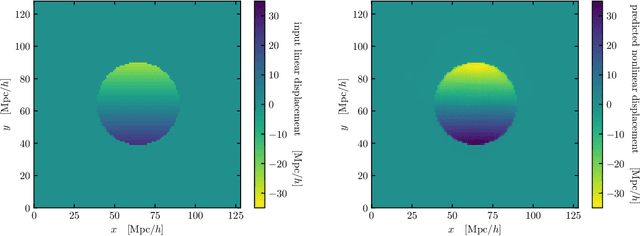
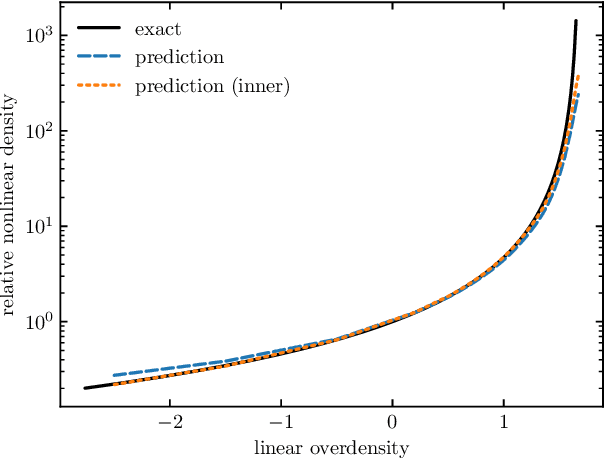
We train a neural network model to predict the full phase space evolution of cosmological N-body simulations. Its success implies that the neural network model is accurately approximating the Green's function expansion that relates the initial conditions of the simulations to its outcome at later times in the deeply nonlinear regime. We test the accuracy of this approximation by assessing its performance on well understood simple cases that have either known exact solutions or well understood expansions. These scenarios include spherical configurations, isolated plane waves, and two interacting plane waves: initial conditions that are very different from the Gaussian random fields used for training. We find our model generalizes well to these well understood scenarios, demonstrating that the networks have inferred general physical principles and learned the nonlinear mode couplings from the complex, random Gaussian training data. These tests also provide a useful diagnostic for finding the model's strengths and weaknesses, and identifying strategies for model improvement. We also test the model on initial conditions that contain only transverse modes, a family of modes that differ not only in their phases but also in their evolution from the longitudinal growing modes used in the training set. When the network encounters these initial conditions that are orthogonal to the training set, the model fails completely. In addition to these simple configurations, we evaluate the model's predictions for the density, displacement, and momentum power spectra with standard initial conditions for N-body simulations. We compare these summary statistics against N-body results and an approximate, fast simulation method called COLA. Our model achieves percent level accuracy at nonlinear scales of $k\sim 1\ \mathrm{Mpc}^{-1}\, h$, representing a significant improvement over COLA.

Field Level Neural Network Emulator for Cosmological N-body Simulations

We build a field level emulator for cosmic structure formation that is accurate in the nonlinear regime. Our emulator consists of two convolutional neural networks trained to output the nonlinear displacements and velocities of N-body simulation particles based on their linear inputs. Cosmology dependence is encoded in the form of style parameters at each layer of the neural network, enabling the emulator to effectively interpolate the outcomes of structure formation between different flat $\Lambda$CDM cosmologies over a wide range of background matter densities. The neural network architecture makes the model differentiable by construction, providing a powerful tool for fast field level inference. We test the accuracy of our method by considering several summary statistics, including the density power spectrum with and without redshift space distortions, the displacement power spectrum, the momentum power spectrum, the density bispectrum, halo abundances, and halo profiles with and without redshift space distortions. We compare these statistics from our emulator with the full N-body results, the COLA method, and a fiducial neural network with no cosmological dependence. We find our emulator gives accurate results down to scales of $k \sim 1\ \mathrm{Mpc}^{-1}\, h$, representing a considerable improvement over both COLA and the fiducial neural network. We also demonstrate that our emulator generalizes well to initial conditions containing primordial non-Gaussianity, without the need for any additional style parameters or retraining.

Predicting the Thermal Sunyaev-Zel'dovich Field using Modular and Equivariant Set-Based Neural Networks

Theoretical uncertainty limits our ability to extract cosmological information from baryonic fields such as the thermal Sunyaev-Zel'dovich (tSZ) effect. Being sourced by the electron pressure field, the tSZ effect depends on baryonic physics that is usually modeled by expensive hydrodynamic simulations. We train neural networks on the IllustrisTNG-300 cosmological simulation to predict the continuous electron pressure field in galaxy clusters from gravity-only simulations. Modeling clusters is challenging for neural networks as most of the gas pressure is concentrated in a handful of voxels and even the largest hydrodynamical simulations contain only a few hundred clusters that can be used for training. Instead of conventional convolutional neural net (CNN) architectures, we choose to employ a rotationally equivariant DeepSets architecture to operate directly on the set of dark matter particles. We argue that set-based architectures provide distinct advantages over CNNs. For example, we can enforce exact rotational and permutation equivariance, incorporate existing knowledge on the tSZ field, and work with sparse fields as are standard in cosmology. We compose our architecture with separate, physically meaningful modules, making it amenable to interpretation. For example, we can separately study the influence of local and cluster-scale environment, determine that cluster triaxiality has negligible impact, and train a module that corrects for mis-centering. Our model improves by 70 % on analytic profiles fit to the same simulation data. We argue that the electron pressure field, viewed as a function of a gravity-only simulation, has inherent stochasticity, and model this property through a conditional-VAE extension to the network. This modification yields further improvement by 7 %, it is limited by our small training set however. (abridged)

Augmenting astrophysical scaling relations with machine learning : application to reducing the SZ flux-mass scatter

Complex systems (stars, supernovae, galaxies, and clusters) often exhibit low scatter relations between observable properties (e.g., luminosity, velocity dispersion, oscillation period, temperature). These scaling relations can illuminate the underlying physics and can provide observational tools for estimating masses and distances. Machine learning can provide a systematic way to search for new scaling relations (or for simple extensions to existing relations) in abstract high-dimensional parameter spaces. We use a machine learning tool called symbolic regression (SR), which models the patterns in a given dataset in the form of analytic equations. We focus on the Sunyaev-Zeldovich flux$-$cluster mass relation ($Y_\mathrm{SZ}-M$), the scatter in which affects inference of cosmological parameters from cluster abundance data. Using SR on the data from the IllustrisTNG hydrodynamical simulation, we find a new proxy for cluster mass which combines $Y_\mathrm{SZ}$ and concentration of ionized gas ($c_\mathrm{gas}$): $M \propto Y_\mathrm{conc}^{3/5} \equiv Y_\mathrm{SZ}^{3/5} (1-A\, c_\mathrm{gas})$. $Y_\mathrm{conc}$ reduces the scatter in the predicted $M$ by $\sim 20-30$% for large clusters ($M\gtrsim 10^{14}\, h^{-1} \, M_\odot$) at both high and low redshifts, as compared to using just $Y_\mathrm{SZ}$. We show that the dependence on $c_\mathrm{gas}$ is linked to cores of clusters exhibiting larger scatter than their outskirts. Finally, we test $Y_\mathrm{conc}$ on clusters from simulations of the CAMELS project and show that $Y_\mathrm{conc}$ is robust against variations in cosmology, astrophysics, subgrid physics, and cosmic variance. Our results and methodology can be useful for accurate multiwavelength cluster mass estimation from current and upcoming CMB and X-ray surveys like ACT, SO, SPT, eROSITA and CMB-S4.

The CAMELS project: public data release

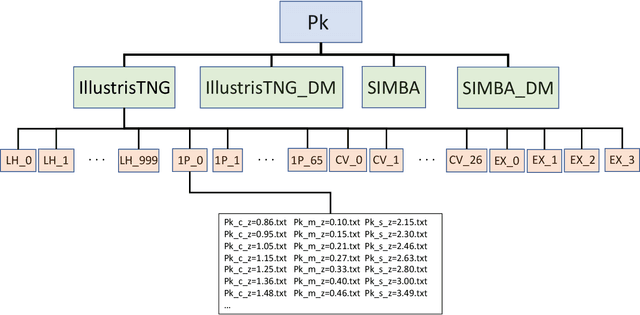
The Cosmology and Astrophysics with MachinE Learning Simulations (CAMELS) project was developed to combine cosmology with astrophysics through thousands of cosmological hydrodynamic simulations and machine learning. CAMELS contains 4,233 cosmological simulations, 2,049 N-body and 2,184 state-of-the-art hydrodynamic simulations that sample a vast volume in parameter space. In this paper we present the CAMELS public data release, describing the characteristics of the CAMELS simulations and a variety of data products generated from them, including halo, subhalo, galaxy, and void catalogues, power spectra, bispectra, Lyman-$\alpha$ spectra, probability distribution functions, halo radial profiles, and X-rays photon lists. We also release over one thousand catalogues that contain billions of galaxies from CAMELS-SAM: a large collection of N-body simulations that have been combined with the Santa Cruz Semi-Analytic Model. We release all the data, comprising more than 350 terabytes and containing 143,922 snapshots, millions of halos, galaxies and summary statistics. We provide further technical details on how to access, download, read, and process the data at \url{https://camels.readthedocs.io}.

Weighing the Milky Way and Andromeda with Artificial Intelligence

We present new constraints on the masses of the halos hosting the Milky Way and Andromeda galaxies derived using graph neural networks. Our models, trained on thousands of state-of-the-art hydrodynamic simulations of the CAMELS project, only make use of the positions, velocities and stellar masses of the galaxies belonging to the halos, and are able to perform likelihood-free inference on halo masses while accounting for both cosmological and astrophysical uncertainties. Our constraints are in agreement with estimates from other traditional methods.

Inferring halo masses with Graph Neural Networks

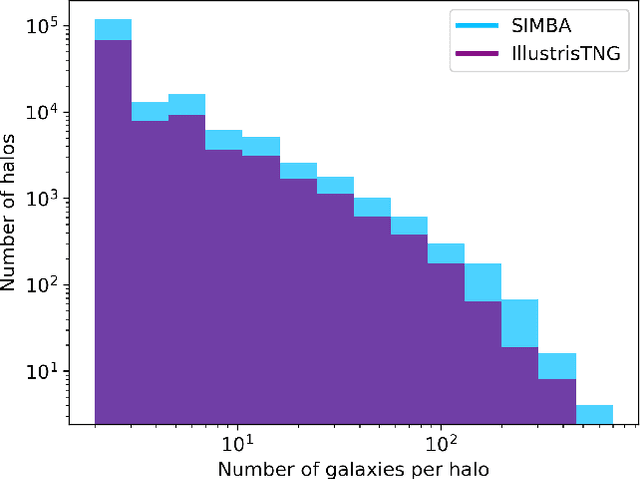
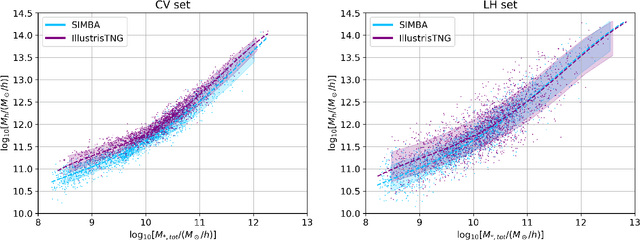
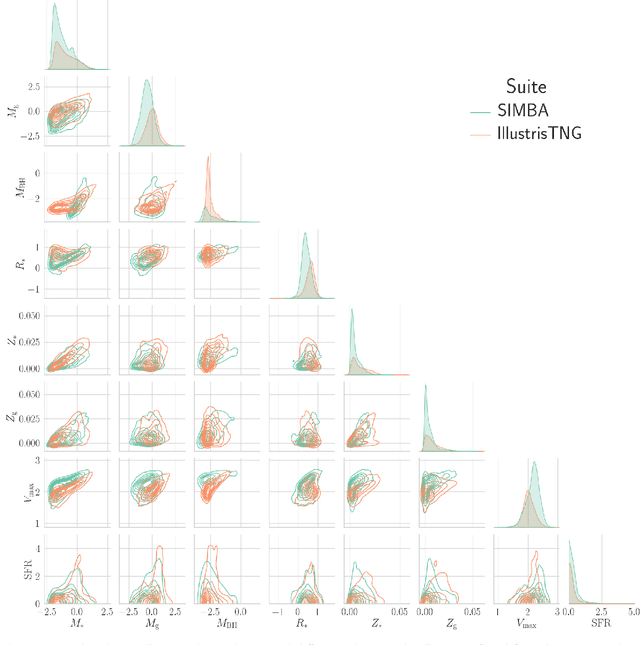
Understanding the halo-galaxy connection is fundamental in order to improve our knowledge on the nature and properties of dark matter. In this work we build a model that infers the mass of a halo given the positions, velocities, stellar masses, and radii of the galaxies it hosts. In order to capture information from correlations among galaxy properties and their phase-space, we use Graph Neural Networks (GNNs), that are designed to work with irregular and sparse data. We train our models on galaxies from more than 2,000 state-of-the-art simulations from the Cosmology and Astrophysics with MachinE Learning Simulations (CAMELS) project. Our model, that accounts for cosmological and astrophysical uncertainties, is able to constrain the masses of the halos with a $\sim$0.2 dex accuracy. Furthermore, a GNN trained on a suite of simulations is able to preserve part of its accuracy when tested on simulations run with a different code that utilizes a distinct subgrid physics model, showing the robustness of our method. The PyTorch Geometric implementation of the GNN is publicly available on Github at https://github.com/PabloVD/HaloGraphNet

The CAMELS Multifield Dataset: Learning the Universe's Fundamental Parameters with Artificial Intelligence

We present the Cosmology and Astrophysics with MachinE Learning Simulations (CAMELS) Multifield Dataset, CMD, a collection of hundreds of thousands of 2D maps and 3D grids containing many different properties of cosmic gas, dark matter, and stars from 2,000 distinct simulated universes at several cosmic times. The 2D maps and 3D grids represent cosmic regions that span $\sim$100 million light years and have been generated from thousands of state-of-the-art hydrodynamic and gravity-only N-body simulations from the CAMELS project. Designed to train machine learning models, CMD is the largest dataset of its kind containing more than 70 Terabytes of data. In this paper we describe CMD in detail and outline a few of its applications. We focus our attention on one such task, parameter inference, formulating the problems we face as a challenge to the community. We release all data and provide further technical details at https://camels-multifield-dataset.readthedocs.io.